Ii. дифференциальные уравнения

1. Дифференциальные уравнения с разделяющими переменными. Задача Коши. Пример. Геометрическая или физическая задача.

2. Однородные дифференциальные уравнения первого порядка. Задача Коши. Пример. Геометрическая или физическая задача.

3. Линейные дифференциальные уравнения первого порядка 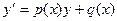. Задача Коши. Пример. Геометрическая или физическая задача.

4. Уравнение Бернулли 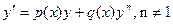. Задача Коши. Пример. Геометрическая или физическая задача.

5. Понижение порядка дифференциального уравнения второго порядка, которое не содержит искомой функции: 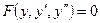. Задача Коши. Пример.

6. Понижение порядка дифференциального уравнения второго порядка, которое не содержит независимой переменной: 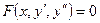. Задача Коши. Пример.

7. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: 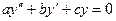. Характеристическое уравнение. Случай, когда дискриминант больше нуля. Общее решение. Задача Коши. Пример. Стабилизация решений.

8. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: 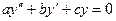. Характеристическое уравнение. Случай, когда дискриминант меньше нуля. Общее решение. Задача Коши. Пример. Стабилизация решений.

9. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: 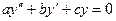. Характеристическое уравнение. Случай, когда дискриминант равен нулю. Общее решение. Задача Коши. Пример. Стабилизация решений.

10. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 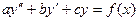. Случай, когда 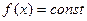и число 0 является корнем характеристического уравнения. Стабилизация решений. Задача Коши. Пример.

11. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 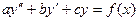. Случай, когда 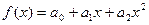и число 0 является корнем характеристического уравнения. Стабилизация решений. Задача Коши. Пример.

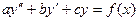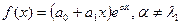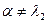12. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами . Случай, когда и . Здесь 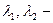корни характеристического уравнения, причем 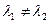. Стабилизация решений. Задача Коши. Пример.

13. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 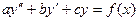. Случай, когда 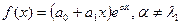и 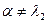. Здесь 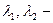корни характеристического уравнения, причем 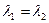. Стабилизация решений. Задача Коши. Пример.

14. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 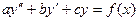. Случай, когда 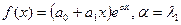и 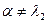. Здесь 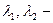корни характеристического уравнения, причем 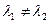. Стабилизация решений. Задача Коши. Пример.

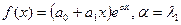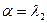15. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и . Здесь 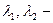корни характеристического уравнения, причем 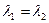. Стабилизация решений. Задача Коши. Пример

16. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 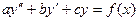. Случай, когда 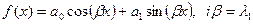или 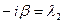. Здесь 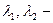корни характеристического уравнения, причем 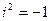. Стабилизация решений. Задача Коши. Пример.

17. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 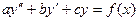. Случай, когда 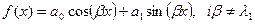и 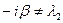. Здесь 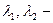корни характеристического уравнения, причем 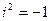. Стабилизация решений. Задача Коши. Пример.

18. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 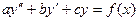. Случай, когда 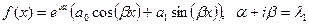или 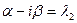. Здесь 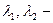корни характеристического уравнения, причем 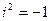. Стабилизация решений. Задача Коши. Пример.

19. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 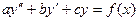. Случай, когда 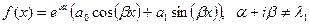и 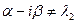. Здесь 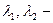корни характеристического уравнения, причем 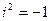. Стабилизация решений. Задача Коши. Пример.

20. Система линейных однородных дифференциальных уравнений.

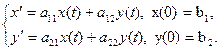
21. Метод исключения. Стабилизация решений.

ЛИТЕРАТУРА