Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами

Дано:

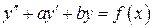, (8)

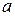и 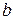– действительные числа, соответствующее однородное уравнение имеет вид:

,

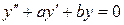характеристическое уравнение будет:

.

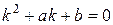При известном общем решении однородного дифференциального уравнения частное решение неоднородного находится вариацией постоянных, а затем составляется общее решение (8). Метод вариацмм применим к (8) при 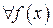и в этом смысле универсален. Однако, для частных случаев 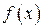чаще применяется метод подбора.

Общее правило. Если 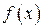может быть представлена в виде

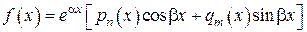, (9)

где 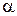, 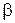– действительные числа, 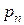и 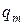– целые рациональные функции степене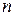й и 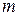, тогда (8) имеет частное решение вида

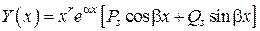. (10)

Здесь 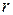– кратность корня 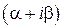характеристического уравнения. Если же 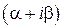не является корнем, то 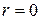. 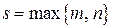, 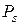и 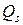– многочлены степени 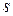. Коэффициенты 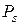и 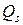определяются из тождества после подстановки 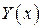в (8). Далее, как обычно, общее решение есть сумма 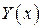и .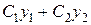

Если же 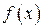не может быть сразу представлена в виде (9), но является суммой таких выражений, то используется теорема о наложении решений.

Для обоснования рассмотрим два частных случая 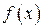и выведем правила нахождения 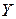для каждого случая.

Случай 1.

, , – .

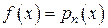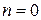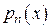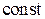Этот случай соответствует 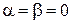. 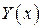будем искать в виде 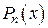. Подставим 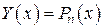в (8), получим

,

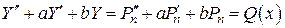где 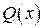есть:

1) многочлен 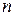-ной степени, если .

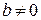2) многочлен 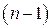-й степени, если , .

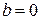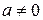3) многочлен 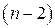-й степени, если .

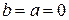В первом случае 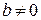приходим к тождеству

, (*)

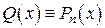из которого можно найти неопределеные коэффициенты .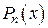

Во втором случае, 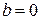, , 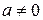то есть когда 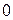есть корень характеристического уравнения, тождество (*) невозможно, так как степень 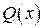на 1 меньше степени 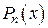. Чтобы их сравнять, надо умножить 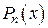на 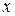. При этом степень 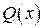повышается на 1. То есть мы будем искать решение в виде

.

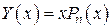В третьем случае 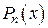умножается на 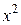, то есть

.

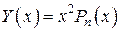Правило 1. Если 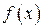есть 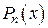, то частное решение 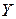надо искать в виде

,

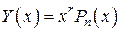где 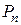– многочлен 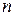-й степени, а 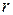– кратность корня 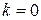. Для вычисления неопределенных коэффициентов 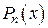надо подставить 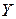в (8) и затем приравнять коэффициенты при одинаковых степенях .

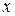Пример.

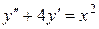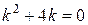, , корень 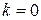– однократный, тогда

,

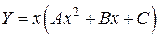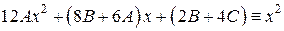
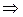
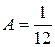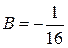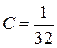, , и

.

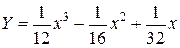Случай 2.

, ,

. (*)

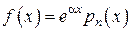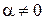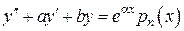Сделаем замену ,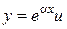

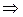
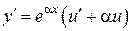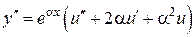
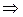
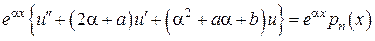
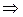
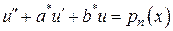, где

, .

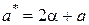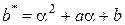Таким образом, уравнение (*) сведено к частному случаю, рассмотренному выше. Следовательно:

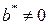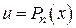
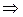
1. Если , тогда 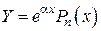, где коэффициенты 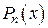следует определить.

2. 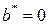, , 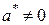то есть если 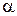– простой корень характеристического уравнения, то .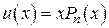

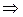
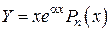3. 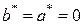, то есть 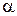– двойной корень характеристического уравнения, то .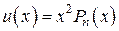

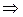
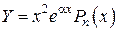Правило 2.

Если 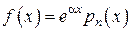, то

,

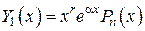где 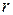– кратность корня 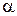в характеристическом уравнении.

Пример.

,

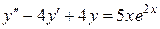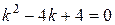
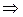
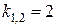
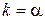и .

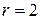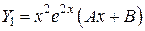, подставляя в дифференциальное уравнение, получим:

, , .

.

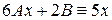
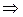
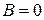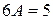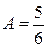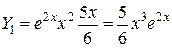Перейдем теперь к общему случаю:

.

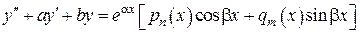Вспомогательная теорема.

Пусть в уравнении

(*)

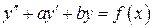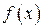– принимает комплексные значения и пусть 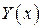– некоторое решение. Тогда

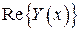есть решение уравнения ,

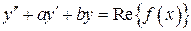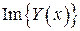есть решение уравнения .

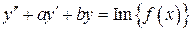Положим 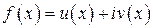, 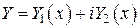. Дважды дифференцируя 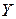и подставляя в (*), получим:

,

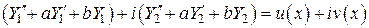отсюда, по равенству комплексных чисел, следует доказательство теоремы.

Следствие.

Если 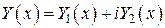есть решение уравнения 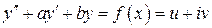, то 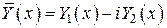есть решение уравнения .

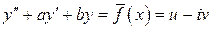Заменим теперь в общем уравнени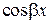и и 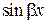по формулам Эйлера:

, ,

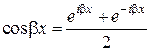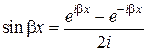перегруппируем и введем новые обозначения:

, , ,

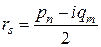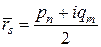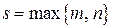тогда

.
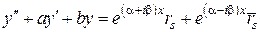