Дифференциальные уравнения первого порядка.

Изучение д.у. 1-го порядка начнем с уравнения, разрешенного относительно производной:

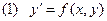
Пусть x и y координаты точки плоскости xOy. Тогда любому решение 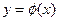соответствует некоторая кривая – график решения. Эти кривые называют интегральными кривыми уравнения (1). Так как 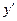есть угловой коэффициент касательной к интегральной кривой в точке M(x,y), то геометрический смысл д.у. 1-го порядка заключается в том, что оно определяет в любой точке ОДЗ направление интегральной кривой, проходящей через эту точку. Другими словами д.у. сопоставляет каждой точке ОДЗ f(x,y) – поле направлений интегральных кривых.

С этой точки зрения Задача Коши заключается в нахождении интегральной кривой, проходящей через заданную точку .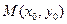

Теорема Коши. Пусть в некоторой окрестности 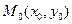правая часть уравнения (1) – f(x,y) является непрерывной функцией x и y и 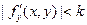. Тогда решение задачи Коши существует и при том является единственным.

Естественно, решение задачи Коши является частным решением (1), когда как совокупность этих решений определяет общее решение.

Покажем, что общее решение (1) содержит одну произвольную постоянную C и является семейством интегральных кривых, зависящих от одного параметра:

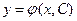
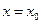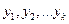Пусть ,а - ординаты некоторых точек на прямой 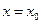, в которых выполняются условия теоремы Коши. Тогда, через любую точку проходит по одной интегральной кривой уравнения (1). Изменяя значение y при 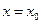мы переходим от одной интегральной кривой к другой. Легко видеть, что при переходе от 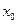к 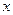в той же области не изменит геометрическую картину, т.к. любая точка на прямой 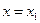также лежит на одной из интегральных кривых, имевших начальную точку на 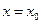. Другими словами при 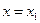мы имеем дело с тем же семейством интегральных кривых. В силу сказанного семейство интегральных кривых зависит только от одного параметра.

Опр. Общим решение д.у. 1-го порядка называют такое его решение, зависящее от C, из которого при соответствующем выборе C можно получить решение любой Задачи Коши, поставленной для данного уравнения в области, где условия теоремы Коши выполняются.

Пример. Уравнение радиоактивного распада

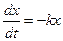имеет решение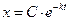

Это решение является общим. Пусть например надо найти решение, которое при 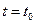принимает значение 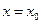. Подставим эти значения в общее решение и найдем C и следовательно задача Коши имеет решение:

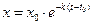
Чтобы представить себе форму и положение интегральных кривых на XOY, часто используют метод изоклин.

Опр. Изоклинами д.у. 1-го порядка называются геометрические места точек плоскости XOY, в которых интегральные кривые имеют одно и то же направление.

Зададим угловой коэффициент интегральных кривых 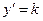, тогда это направление интегральные кривые (1) , будут иметь в точках XOY, удовлетворяющих уравнению:

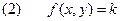
т.е. уравнение (2) есть уравнение изоклины. Поскольку k- выбрано произвольно, то (2) определяет семейство изоклин д.у. (1).

Пусть теперь построена последовательность изоклин, соответствующих

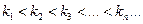Причем 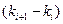достаточно малое число. Выберем на изоклинах 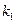ряд точек и проведем из них отрезки прямых с угловым коэффициентом 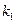до пересечения с изоклиной соответствующей 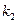. Из получившихся точек пресечения - до 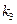с коэффициентом 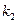и т.д.. Эти отрезки образуют ряд ломанных, которые дают приближенное изображение интегральных кривых заданного уравнения. В самом деле, любой отрезок ломанной есть отрезок касательной к некоторой точке интегральной кривой и на малом отрезке аппроксимирует эту кривую. Чем меньше значение 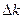, тем короче отрезки ломанных и тем лучше ломанная представляет кривую.

Как было сказано выше, д.у. 1-го порядка соответствует семейство интегральных кривых, зависящее от одного параметра C. Важно и обратное утверждение – любому однопараметрическому семейству кривых, если их уравнение дифференцируемо по x, соответствует некоторое д.у..

Пусть такое семейство задано уравнением:

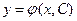(2)

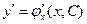тогда (3).

Исключая из (2) и (3) C получим :

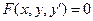(4)

Если удается выразить C из (2) как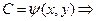

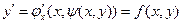(4*)

Полученное д.у. называют д.у. семейства (2) : оно описывает обычно некоторое геометрическое свойство, общее для всех кривых данного семейства. Исходное же уравнение (2) определяет общее решение д.у. вида (4) или (4*), т.к. 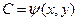найдено из равенства 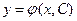, то 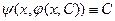, а следовательно 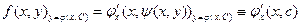т.е. 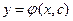при подстановке в (4*) обращает его в тождество.