Простейшие дифференциальные уравнения и
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Краткий курс лекций
Составитель Ю.В.Обрубов
Калуга - 2012
Простейшие дифференциальные уравнения и
Методы их интегрирования.
Опр. Дифференциальными уравнениями называются уравнения, содержащие неизвестные функции, их аргументы и производные от неизвестных функций по этим аргументам, или дифференциалы неизвестных функций. Д.у. называется обыкновенным, если неизвестные функции зависят только от одной переменной.
(1) F(x,y,y’, … , y(n) ) = 0:
(2) Ф(x,y,dy, … , , d(n) y ) = 0.
Примеры.
Основные понятия теории дифференциальных уравнений.
Порядок старшей входящей в уравнение производной определяет порядок уравнения - n.
Любая функция, которая при подстановке в уравнение вместо неизвестной обращает его в тождество, называется решение этого уравнения. Например, sin(x) есть решение уравнения второго порядка 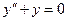 . Дифференциальные уравнения имеют бесконечное множество решений, если имеется хотя бы одно. Обычно, при решении ставиться задача нахождения всех его решений. Процесс решения д.у. часто называют интегрирование д.у.. Если же решается конкретная задача (в физике, технике и т.д.) по нахождению решения д.у., то на неизвестную функцию налагаются как правило дополнительные условия. Например, функция должна принимать определенные значения при заданных значениях аргумента. Такие условия называют начальными условиями, а конкретное решение – частным решением д.у..
. Дифференциальные уравнения имеют бесконечное множество решений, если имеется хотя бы одно. Обычно, при решении ставиться задача нахождения всех его решений. Процесс решения д.у. часто называют интегрирование д.у.. Если же решается конкретная задача (в физике, технике и т.д.) по нахождению решения д.у., то на неизвестную функцию налагаются как правило дополнительные условия. Например, функция должна принимать определенные значения при заданных значениях аргумента. Такие условия называют начальными условиями, а конкретное решение – частным решением д.у..
Совокупность всех частных решений называют общим решением. Отметим, что общее решение д.у. n-го порядка содержит n произвольных констант, т.е. имеет вид:
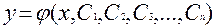
Для уравнения n-го порядка начальные условия чаще всего задаются следующим образом:
требуется найти решение д.у., которое при заданном значении 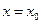 принимает вместе со своими производными вплоть до (n-1) порядка, наперед заданные значения:
принимает вместе со своими производными вплоть до (n-1) порядка, наперед заданные значения:
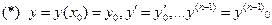 при
при 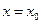 .
.
Задача о решении д.у., удовлетворяющем начальным условия вида (*) называется задачей Коши.
Для уравнения 1-го порядка задача Коши сводится к поиску решения, которое при 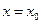 принимает значение
принимает значение 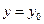 .
.
Существование ФСР (2)
Теорема:
Любое однородное линейное дифференциальное уравнение имеет фундаментальную систему решений.
Доказательство:
Рассмотрим дифференциальное уравнение
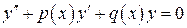
и две системы начальных условий:
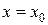 ,
, 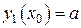 ,
, 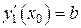 ,
,
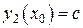 ,
, 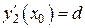 ,
,
где
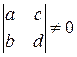 .
.
Пусть 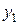 и
и 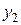 – частные решения соответствующих задач Коши. Докажем, что они образуют фундаментальную систему:
– частные решения соответствующих задач Коши. Докажем, что они образуют фундаментальную систему:
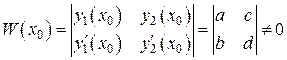 .
.
Теорема доказана.
Основная теорема:
Общее решение линейного однородного дифференциального уравнения 2-го порядка является линейной комбинацией с произвольными постоянными коэффициентами любых двух решений этого уравнения, образующих фундаментальную систему решений. Другими словами, общее решение линейного однородного дифференциального уравнения 2-го порядка есть сумма двух частных решений линейно независимых решений, умноженных на произвольные постоянные.
Доказательство:
Пусть 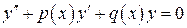 и
и 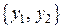 – фундаментальная система решений. Составим линейную комбинацию
– фундаментальная система решений. Составим линейную комбинацию
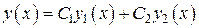 ,
,
где 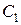 ,
, 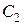 есть произвольные постоянные. Надо доказать, что любое частное решение можно получить из
есть произвольные постоянные. Надо доказать, что любое частное решение можно получить из 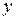 выбором
выбором 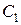 и
и 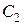 .
.
Пусть 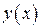 есть решение задачи Коши для начальных условий
есть решение задачи Коши для начальных условий
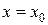 ,
, 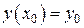 ,
, 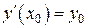 .
.
Положим 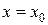 , тогда
, тогда
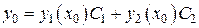 ,
,
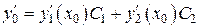 ,
,
отсюда
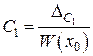 и
и 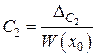 .
.
Так как 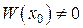 , то
, то 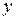 и есть общее решение.
и есть общее решение.
Теоремы о частных решениях
Рассмотрим неоднородное уравнение
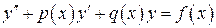 (1)
(1)
и соответствующее однородное уравнение
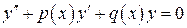 . (2)
. (2)
Теорема 1:
Разность любых двух частных решений уравнения (1) есть частное решение соответствующего однородного дифференциального уравнения.
Доказательство:
Пусть 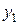 и
и 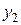 – частные решения уравнения (1). Подставим в соответствующее однородное дифференциальное уравнение функцию
– частные решения уравнения (1). Подставим в соответствующее однородное дифференциальное уравнение функцию 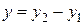 вместе с ее производными:
вместе с ее производными:
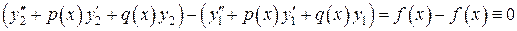 .
.
Теорема доказана.
Теорема 2:
Если 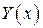 – частное решение уравнения (1),
– частное решение уравнения (1), 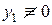 – частное решение соответствующего однородного уравнения, то
– частное решение соответствующего однородного уравнения, то
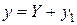
есть новое частное решение уравнения (1).
Доказательство:
Справедливы следующие соотношения:
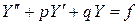 ,
,
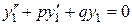 ,
,
значит,
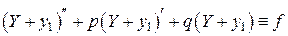 .
.
Теорема доказана.
Из теорем 1 и 2 следует, что, взяв любое одно частное решение неоднородного уравнения (1) и прибавляя всевозможные частные решения однородного уравнения (2), получим все без исключения частные решения уравнения (1).
Определение: Общее решение 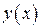 неоднородного линейного дифференциального уравнения 2-го порядка есть сумма любого частного решения данного уравнения и общего решения соответствующего однородного линейного дифференциального уравнения 2-го порядка:
неоднородного линейного дифференциального уравнения 2-го порядка есть сумма любого частного решения данного уравнения и общего решения соответствующего однородного линейного дифференциального уравнения 2-го порядка:
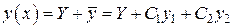 ,
,
где 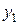 и
и 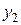 есть линейно независимые частные решения уравнения (2).
есть линейно независимые частные решения уравнения (2).
Теорема 3:
Если правая часть уравнения (1) есть сумма двух функций 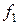 и
и 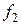 , и если
, и если 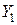 есть частное решение уравнения (1) с правой частью
есть частное решение уравнения (1) с правой частью 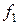 , а
, а 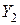 – частное решение уравнения (1) с правой частью
– частное решение уравнения (1) с правой частью 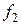 , то
, то 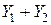 – частное решение уравнения (1) с правой частью
– частное решение уравнения (1) с правой частью 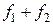 .
.
Доказательство:
Рассмотрим уравнение 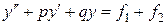 , подставим
, подставим 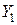 и
и 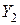 в уравнения
в уравнения 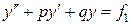 и
и 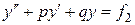 соответственно. После сложения последних уравнений и группировки слагаемых получим:
соответственно. После сложения последних уравнений и группировки слагаемых получим:
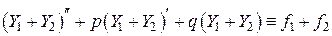 .
.
Теорема доказана.
Пример:
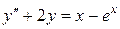 , (1)
, (1)
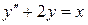 ,
, 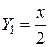 , (2)
, (2)
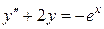 ,
, 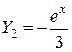 . (3)
. (3)
Тогда 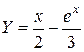 – частное решение уравнения (1).
– частное решение уравнения (1).
Случай 1.
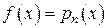 ,
, 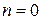 ,
, 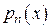 –
– 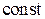 .
.
Этот случай соответствует 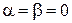 .
. 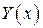 будем искать в виде
будем искать в виде 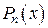 . Подставим
. Подставим 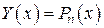 в (8), получим
в (8), получим
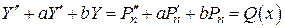 ,
,
где 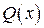 есть:
есть:
1) многочлен 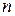 -ной степени, если
-ной степени, если 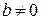 .
.
2) многочлен 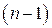 -й степени, если
-й степени, если 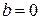 ,
, 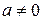 .
.
3) многочлен 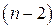 -й степени, если
-й степени, если 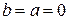 .
.
В первом случае 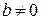 приходим к тождеству
приходим к тождеству
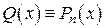 , (*)
, (*)
из которого можно найти неопределеные коэффициенты 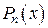 .
.
Во втором случае, 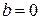 ,
, 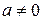 , то есть когда
, то есть когда 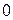 есть корень характеристического уравнения, тождество (*) невозможно, так как степень
есть корень характеристического уравнения, тождество (*) невозможно, так как степень 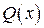 на 1 меньше степени
на 1 меньше степени 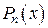 . Чтобы их сравнять, надо умножить
. Чтобы их сравнять, надо умножить 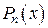 на
на 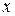 . При этом степень
. При этом степень 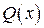 повышается на 1. То есть мы будем искать решение в виде
повышается на 1. То есть мы будем искать решение в виде
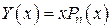 .
.
В третьем случае 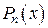 умножается на
умножается на 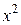 , то есть
, то есть
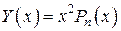 .
.
Правило 1. Если 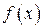 есть
есть 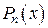 , то частное решение
, то частное решение 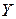 надо искать в виде
надо искать в виде
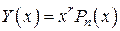 ,
,
где 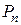 – многочлен
– многочлен 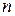 -й степени, а
-й степени, а 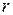 – кратность корня
– кратность корня 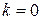 . Для вычисления неопределенных коэффициентов
. Для вычисления неопределенных коэффициентов 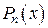 надо подставить
надо подставить 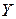 в (8) и затем приравнять коэффициенты при одинаковых степенях
в (8) и затем приравнять коэффициенты при одинаковых степенях 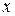 .
.
Пример.
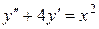 ,
, 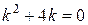 , корень
, корень 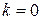 – однократный, тогда
– однократный, тогда
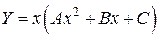 ,
,
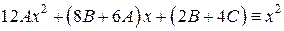
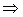
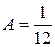 ,
, 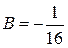 ,
, 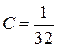 и
и
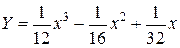 .
.
Случай 2.
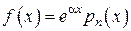 ,
, 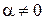 ,
,
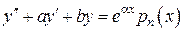 . (*)
. (*)
Сделаем замену 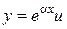
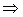
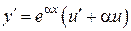 ,
, 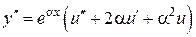
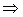
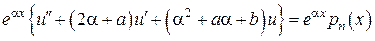
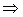
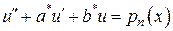 , где
, где
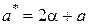 ,
, 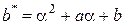 .
.
Таким образом, уравнение (*) сведено к частному случаю, рассмотренному выше. Следовательно:
1. Если 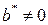 , тогда
, тогда 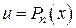
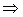
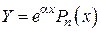 , где коэффициенты
, где коэффициенты 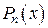 следует определить.
следует определить.
2. 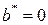 ,
, 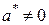 , то есть если
, то есть если 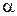 – простой корень характеристического уравнения, то
– простой корень характеристического уравнения, то 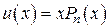
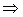
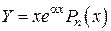 .
.
3. 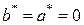 , то есть
, то есть 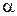 – двойной корень характеристического уравнения, то
– двойной корень характеристического уравнения, то 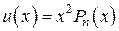
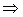
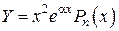 .
.
Правило 2.
Если 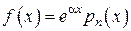 , то
, то
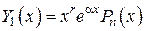 ,
,
где 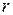 – кратность корня
– кратность корня 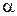 в характеристическом уравнении.
в характеристическом уравнении.
Пример.
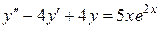 ,
,
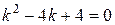
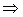
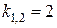
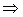
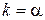 и
и 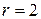 .
.
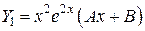 , подставляя в дифференциальное уравнение, получим:
, подставляя в дифференциальное уравнение, получим:
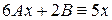
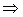
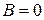 ,
, 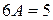 ,
, 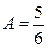 .
.
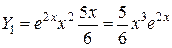 .
.
Перейдем теперь к общему случаю:
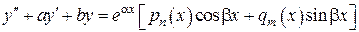 .
.
Вспомогательная теорема.
Пусть в уравнении
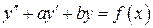 (*)
(*)
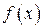 – принимает комплексные значения и пусть
– принимает комплексные значения и пусть 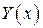 – некоторое решение. Тогда
– некоторое решение. Тогда
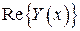 есть решение уравнения
есть решение уравнения 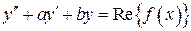 ,
,
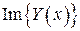 есть решение уравнения
есть решение уравнения 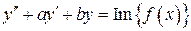 .
.
Положим 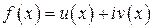 ,
, 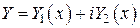 . Дважды дифференцируя
. Дважды дифференцируя 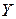 и подставляя в (*), получим:
и подставляя в (*), получим:
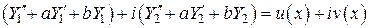 ,
,
отсюда, по равенству комплексных чисел, следует доказательство теоремы.
Следствие.
Если 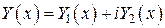 есть решение уравнения
есть решение уравнения 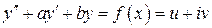 , то
, то 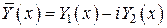 есть решение уравнения
есть решение уравнения 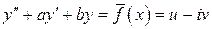 .
.
Заменим теперь в общем уравнении 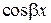 и
и 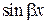 по формулам Эйлера:
по формулам Эйлера:
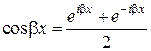 ,
, 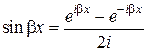 ,
,
перегруппируем и введем новые обозначения:
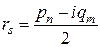 ,
, 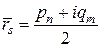 ,
, 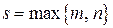 ,
,
тогда
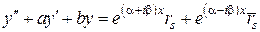 .
.
Замечание.
При использовании (**) надо помнить, что вид 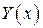 подобен виду
подобен виду 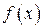 , но является более полным. Так, если
, но является более полным. Так, если 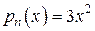 , то в (**) мы должны брать
, то в (**) мы должны брать 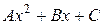 , если
, если 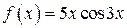 , то в (**) следует взять
, то в (**) следует взять 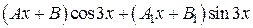 , и если
, и если 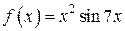 , то в (**) возьмем
, то в (**) возьмем 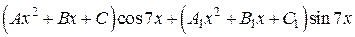 , и т. д.
, и т. д.
Пример.
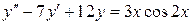 ,
,
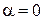 ,
, 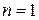 ,
, 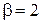 ,
, 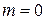 ,
,
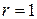 , так как
, так как 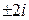 не корень характеристического уравнения,
не корень характеристического уравнения,
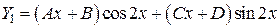 ,
,
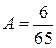 ,
, 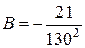 ,
, 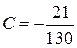 ,
, 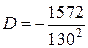 , и т. д.
, и т. д.
9.4.3. Линейные дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами
Теорема.
Линейное дифференциальное уравнение преобразуется снова в линейное дифференциальное уравнение при всяком линейном преобразовании неизвестной функции и любом преобразовании аргумента (и только при таких преобразованиях).
Доказательство.
В уравнении
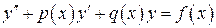
положим 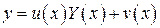 , где
, где 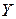 – новая искомая функция, а
– новая искомая функция, а 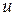 и
и 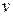 – известные функции. Тогда
– известные функции. Тогда
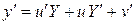 ,
,
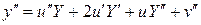 ,
,
и исходное уравнение преобразуется к виду
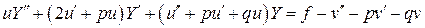 ,
,
и это уравнение снова является линейным, так как все коэффициенты и правая часть есть функции только 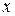 . отметим, что
. отметим, что 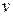 входит только в правую часть.
входит только в правую часть.
Положим, что 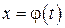 , тогда
, тогда 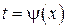 и
и
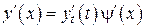 ,
, 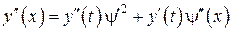 .
.
Подставляя эти значения, получим опять линейное уравнение:
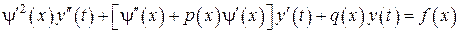 ,
,
заменяя 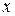 на
на 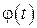 найдем, что все коэффициенты и правая часть есть функции только
найдем, что все коэффициенты и правая часть есть функции только 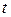 . На этом доказательство первой части закончено.
. На этом доказательство первой части закончено.
Предположим теперь, что 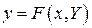 . Тогда
. Тогда
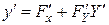 ,
, 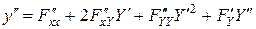 .
.
Подставляя 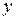 ,
, 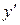 и
и 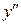 в исходное уравнение, получим в общем случае нелинейное уравнение
в исходное уравнение, получим в общем случае нелинейное уравнение
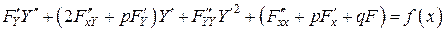 . (*)
. (*)
Чтобы (*) было линейным, нужно, чтобы 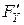 и
и 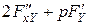 не зависели от
не зависели от 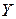 ,
, 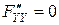 , а
, а 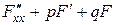 содержало
содержало 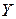 лишь в первой степени или было функцией только от
лишь в первой степени или было функцией только от 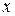 . Выполнение этих требований превращает
. Выполнение этих требований превращает 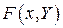 в линейную функцию. Если
в линейную функцию. Если
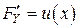
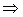
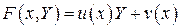 ,
,
и тогда 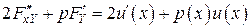 не зависит от
не зависит от 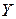 , а
, а 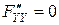 . При этом
. При этом
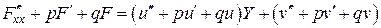
есть функция от 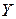 в первой степени. Таким образом, теорема доказана.
в первой степени. Таким образом, теорема доказана.
Очевидно, что для преобразования линейного дифференциального уравнения с переменными коэффициентами в линйое дифференциальное уравнение с постоянными коэффициентами достаточно рассмотреть соответствующее однородное уравнение.
Согласно теореме, сохранение линейности возможно только в двух случаях: при линейном преобразовании функции 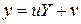 (
( 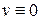 , так как она не входит в коэффициенты в левой части) и при произвольном преобразовании
, так как она не входит в коэффициенты в левой части) и при произвольном преобразовании 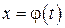 .
.
Теперь выведем условия, налагаемые на 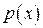 и
и 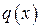 линейного дифференциального уравнения 2-го порядка, при которых это уравнение может быть приведено к линейному дифференциальному уравнению 2-го порядка с постоянными коэффициентами с помощью преобразования
линейного дифференциального уравнения 2-го порядка, при которых это уравнение может быть приведено к линейному дифференциальному уравнению 2-го порядка с постоянными коэффициентами с помощью преобразования 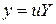 или
или 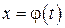 .
.
Необходимое и достаточное условие для преобразования 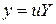 .
.
Итак, пусть дано уравнение
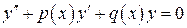 (1)
(1)
и подстановка 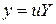 , тогда
, тогда
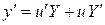 ,
,
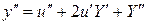 ,
,
подставляя в уравнение, получим:
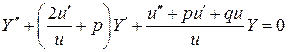 , (2)
, (2)
и потребуем, чтобы коэффициенты при 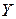 и
и 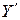 были константами:
были константами:
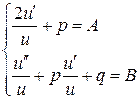 .
.
Тогда 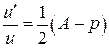 . Отсюда
. Отсюда 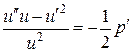 или
или
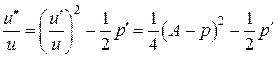
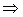
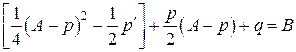 или
или
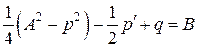 .
.
Последнее равенство можно записать, как
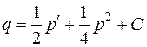 , где
, где 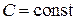 . (3)
. (3)
(3) и есть условие приводимости (1) к (2), в котором коэффициенты являются постоянными.
Найдем теперь 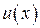 , с помощью которой это приведение выполняется:
, с помощью которой это приведение выполняется:
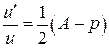
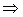
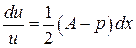
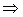
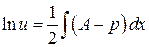
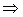
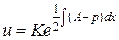 .
.
Положим 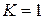 и
и 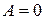 , тогда
, тогда 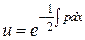 и
и
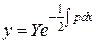 .
.
Таким образом, преобразование выполняется, если выполнено (3).
Пример.
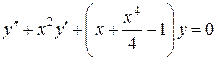 .
.
Условие (3) выполняется и 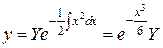 приводит к уравнению
приводит к уравнению
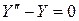 .
.
Необходимое и достаточное условие для преобразования 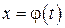 .
.
Пусть 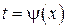 , тогда
, тогда
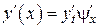 и
и 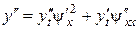
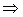
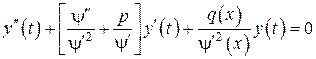 . (
. ( 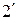 )
)
Далее,
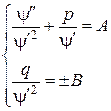

Из (*), считая 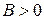 , имеем
, имеем 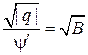
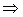
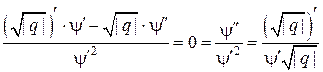 .
.
Кроме того, 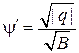 . Подставляя эти результаты в (**), получим:
. Подставляя эти результаты в (**), получим:
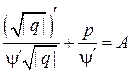 или
или 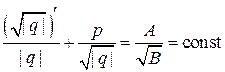 ,
,
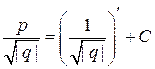 . (
. ( 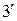 )
)
( 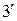 ) и есть искомое условие.
) и есть искомое условие.
Найдем теперь 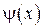 . Из (*):
. Из (*):
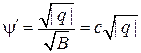
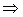
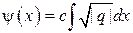
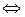
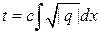 ,
,
где 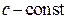 , а
, а 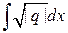 – одна из первообразных от
– одна из первообразных от 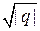 .
.
Таким образом, если выполняется ( 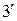 ), то (1) можно привести к уравнению с постоянными коэффициентами с помощью преобразования
), то (1) можно привести к уравнению с постоянными коэффициентами с помощью преобразования 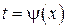 .
.
Пример. Рассмотрим уравнение Эйлера
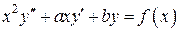 ,
,
здесь 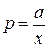 ,
, 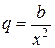 ,
, 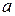 ,
, 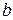 –
– 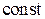 , тогда
, тогда 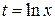 или
или 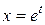 – нужная подстановка.
– нужная подстановка.
Теорема 1.
Если линейное дифференциальное уравнение 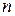 -го порядка
-го порядка
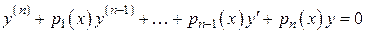 (*)
(*)
допускает приведение к дифференциальному уравнению с постоянными коэффициентами при помощи замены независимой переменной 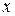 вида
вида 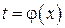 , то такой цели служит только подстановка
, то такой цели служит только подстановка
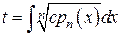 , где
, где 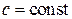 .
.
Теорема 2.
Если (*) допускает приведение к дифференциальному уравнению с постоянными коэффициентами при помощи подстановки 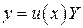 , преобразующей неизвестную функцию
, преобразующей неизвестную функцию 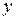 , то такое преобразование выполняется только, если положить
, то такое преобразование выполняется только, если положить
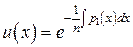
Для неоднородных линейных дифференциальных уравнений приведение осуществляется по тем же формулам.
Теорема Коши.
Если 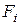 – непрерывные функции по
– непрерывные функции по 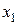 ,
, 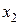 , …,
, …, 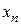 в некоторой области
в некоторой области 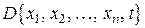 , то любой внутренней точке
, то любой внутренней точке 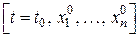 области
области 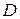 соответствует, и притом единственное, решение
соответствует, и притом единственное, решение 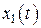 ,
, 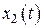 , …,
, …, 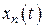 , удовлетворяюще этим начальным условиям. Такое решение называется частным.
, удовлетворяюще этим начальным условиям. Такое решение называется частным.
Произвольно изменяя 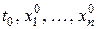 , получим бесконечное множество решений, или:
, получим бесконечное множество решений, или:
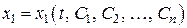 , …,
, …, 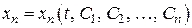
– такое решение называется общим. Частное решение всегда можно получить из общего.
Системы дифференциальных уравнений типа (1) и дифференциальные уравнения 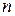 -го порядка можно преобразовывать друг в друга с помощью введения дополнительных переменных или их исключения.
-го порядка можно преобразовывать друг в друга с помощью введения дополнительных переменных или их исключения.
Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид:
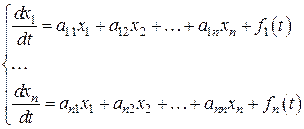 (2)
(2)
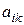 – действительные числа,
– действительные числа, 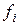 – известные непрерывные функции. Если
– известные непрерывные функции. Если 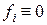 , то система называется однородной.
, то система называется однородной.
Рассмотрим метод интегрирования системы (2) приведением е к одному линейному дифференциальному уравнению 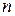 -го порядка с одной искомой функцией
-го порядка с одной искомой функцией 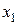 (например). Для этого продифференцируем первое уравнение из (2) по
(например). Для этого продифференцируем первое уравнение из (2) по 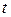 и заменим получившиеся в правой части
и заменим получившиеся в правой части 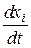 их выражениями из (2):
их выражениями из (2):
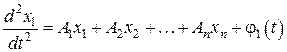 .
.
Затем продифференцируем и его по 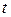 и снова сделаем замены. После
и снова сделаем замены. После 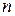 -го шага получим систему:
-го шага получим систему:
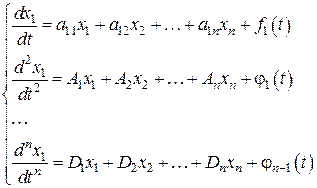 (*)
(*)
Выражая из первых 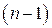 уравнений
уравнений 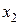 ,
, 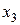 , …,
, …, 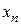 через
через 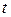 ,
, 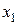 ,
, 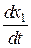 ,
, 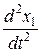 , …,
, …, 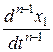 (предполагая
(предполагая 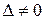 ) и подставляя в
) и подставляя в 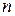 -е уравнение, получим
-е уравнение, получим
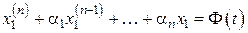 (**)
(**)
– линейное дифференциальное уравнение 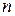 -го порядка с постоянными коэффициентами и одной неизвестной функцией.
-го порядка с постоянными коэффициентами и одной неизвестной функцией.
Найдя общее решение (**) 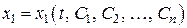 и используя производные
и используя производные 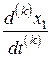 от него из (*) найдем
от него из (*) найдем 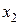 ,
, 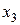 , …,
, …, 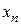 .
.
Пример.
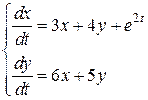 ,
,
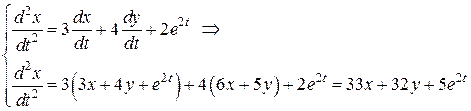
Получим систему
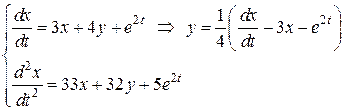 ,
,
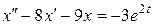
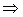
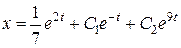 .
.
Дифференцируя 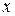 и подставляя в
и подставляя в 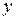 , найдем:
, найдем:
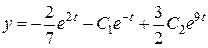 .
.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Краткий курс лекций
Составитель Ю.В.Обрубов
Калуга - 2012
Простейшие дифференциальные уравнения и
Методы их интегрирования.
Опр. Дифференциальными уравнениями называются уравнения, содержащие неизвестные функции, их аргументы и производные от неизвестных функций по этим аргументам, или дифференциалы неизвестных функций. Д.у. называется обыкновенным, если неизвестные функции зависят только от одной переменной.
(1) F(x,y,y’, … , y(n) ) = 0:
(2) Ф(x,y,dy, … , , d(n) y ) = 0.
Примеры.
Основные понятия теории дифференциальных уравнений.
Порядок старшей входящей в уравнение производной определяет порядок уравнения - n.
Любая функция, которая при подстановке в уравнение вместо неизвестной обращает его в тождество, называется решение этого уравнения. Например, sin(x) есть решение уравнения второго порядка 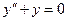 . Дифференциальные уравнения имеют бесконечное множество решений, если имеется хотя бы одно. Обычно, при решении ставиться задача нахождения всех его решений. Процесс решения д.у. часто называют интегрирование д.у.. Если же решается конкретная задача (в физике, технике и т.д.) по нахождению решения д.у., то на неизвестную функцию налагаются как правило дополнительные условия. Например, функция должна принимать определенные значения при заданных значениях аргумента. Такие условия называют начальными условиями, а конкретное решение – частным решением д.у..
. Дифференциальные уравнения имеют бесконечное множество решений, если имеется хотя бы одно. Обычно, при решении ставиться задача нахождения всех его решений. Процесс решения д.у. часто называют интегрирование д.у.. Если же решается конкретная задача (в физике, технике и т.д.) по нахождению решения д.у., то на неизвестную функцию налагаются как правило дополнительные условия. Например, функция должна принимать определенные значения при заданных значениях аргумента. Такие условия называют начальными условиями, а конкретное решение – частным решением д.у..
Совокупность всех частных решений называют общим решением. Отметим, что общее решение д.у. n-го порядка содержит n произвольных констант, т.е. имеет вид:
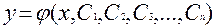
Для уравнения n-го порядка начальные условия чаще всего задаются следующим образом:
требуется найти решение д.у., которое при заданном значении 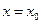 принимает вместе со своими производными вплоть до (n-1) порядка, наперед заданные значения:
принимает вместе со своими производными вплоть до (n-1) порядка, наперед заданные значения:
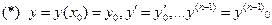 при
при 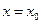 .
.
Задача о решении д.у., удовлетворяющем начальным условия вида (*) называется задачей Коши.
Для уравнения 1-го порядка задача Коши сводится к поиску решения, которое при 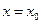 принимает значение
принимает значение 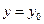 .
.
