Упражнение в парах «Сколько-сколько?»

Каждой паре предлагается придумать задачу «О себе» и затем между собой разыграть диалог. Сна­чала первый ученик называет исходное число пред­метов, второй — указывает, на сколько у него таких предметов больше или меньше. Например:

— У меня 3 наклейки. А сколько у тебя?

— А у меня на 2 наклейки больше.

Затем изменяется порядок высказываний: первым число предметов называет второй ученик, а первый указывает, на сколько у него таких предметов соот­ветственно меньше или больше, т.е. составляется обратная задача:

— У меня 5 наклеек. А сколько у тебя?

— А у меня на 2 наклейки меньше.

После прослушивания диалогов следует сделать вывод: «Если у первого предметов больше, чем у второго, то у второго — на столько же меньше, чем у первого», который можно обобщить в виде схемы.

Учитель напоминает учащимся о Знайке — коро­тышке из Цветочного города, — который научился из одной задачи составлять ещё одну.

На доске демонстрируется первая часть динами­ческой таблицы, и учитель знакомит учащихся с усло­вием задачи о маках и ромашках: «Синеглазка поса­дила на клумбе 20 маков. Ромашек — на 4 меньше. Сколько ромашек посадила Синеглазка на клумбе?».

Учащимся предлагается заполнить пропуски в краткой записи задачи и решить задачу устно. После этого учитель сообщает, что, используя уже решённую задачу, можно составить ещё одну — обратную, — за­дачу о ромашках и маках, и

демонстрирует вторую часть динамической таблицы.

Учитель обращает внимание учащихся, что теперь известно, сколько ромашек посадила Синеглазка (начинается заполнение второй части динамической таблицы), и предлагает определить, больше или меньше маков по сравнению с ромашками высажено.
Учащимся предлагается переформулировать фразу «Ромашек — на 4 меньше, чем маков»: «Маков — на…, чем ромашек». Затем требуется составить обратную задачу, используя известное число ромашек и соотношение между числом ромашек и

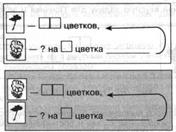
числом маков. Необходимо обратить внимание уча­щихся, что вопрос обратной задачи должен содержать «обратное» требование: определить число маков.

Подводя итог, полезно сравнить схемы прямой и обратной задач и повторить, как получить новую (об­ратную) задачу из данной (прямой).

Затем учащимся предлагается новая задача. Тре­буется решить эту задачу и составить обратную. При этом выполнение задания можно организовать в за­висимости от уровня математической подготовки уча­щихся: фронтально, в парах или индивидуально.

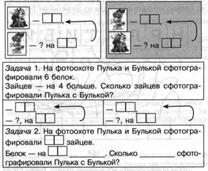
Примерное условие задачи для фронтальной (пар­ной, индивидуальной) работы: «На фотоохоте Пулька и Булькой сфотографировали 6 белок. Зайцев — на 4 больше. Сколько зайцев сфотографировали Пулька с Булькой?».

Образец динамической таблицы для фронтального выполнения задания.

Переменка 2

Дыхательная гимна­стика.

Упражнение «Составь задачу»

Каждый ученик получает карточку «Составь задачу». Требуется составить одну или несколько задач (по выбору ученика). При выполнении задания можно ограничиться заполнением схемы и записью вопроса или, заполнив схему, записать полное усло­вие (по усмотрению учителя).

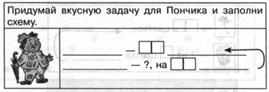
В процессе выполнения задания учитель просма­тривает заполненные схемы и составленные задачи, корректируя работу учащихся.

После выполнения заданий можно провести кон­курс и определить самую «вкусную», самую «слад­кую», самую «витаминную» задачи.

Занятие 26. Лабиринты. Математические игры с цифрами и числами

Цель: планируется, что к окончанию занятия учащиеся будут знать:оновых видах математических задач: лабиринтах, математи­ческих играх; уметь: решать новые виды математических задач: лабиринты, математи­ческие игры.

Оборудование: рисунок «Разгадай слово», схемы лабиринтов «Мышь и сыр», «Утка и утята», «Колобок», карточки для игры «Найдите пару», изображения Чипа и Дейла, карточки с изображениями орехов, таблица, цветные мелки (маркеры); по 11 счётных палочек (для каждой пары учащихся), по 2-3 рисунка со схемами лабиринтов (для каждого ученика).

Ход занятия

Разминка

Учащимся демонстрируется рисунок «Разгадай сло­во» и предлагается установить, в какой клет­ке должна находиться каждая из записанных букв:

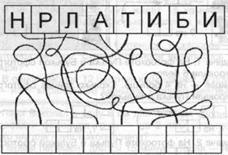
Чтобы предупредить угадывание ответа, буквы слова «ЛАБИРИНТ» записаны справа налево — «ТНИРИБАЛ».

Интересно знать

Лабиринт — это сложное сооружение с запутан­ными ходами.

Один из древнегреческих мифов повествует о ла­биринте, в котором находился Минотавр — чудовище с телом великана и головой быка. Юноши и девушки, попадавшие в лабиринт, не найдя обратной дороги, становились жертвами Минотавра. И только отважный древнегреческий герой Тесей смог войти в лабиринт, победить Минотавра и вернуться обратно. Выйти из лабиринта Тесею помог клубок ниток.

Желательно обсудить с учащимися, как это могло быть. (Конец нити Тесей закрепил при входе в лаби­ринт. Продвигаясь по лабиринту, он разматывал клу­бок, а потом по этой нити и нашёл выход.) Чтобы спорилось нужное дело, Чтобы в жизни не знать неудач, В лабиринт отправляемся смело — В мир загадок и сложных задач. Упражнение «Пройди лабиринт» Учитель сообщает, что лабиринты изображают в виде схем, и демонстрирует несколько лабиринтов.

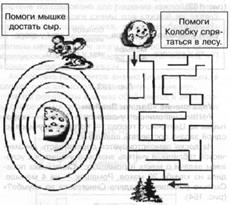
При этом надо объяснить, что возможны различные задания:

- найти маршрут от входа к центру лабиринта,

- найти выход из лабиринта,

- пройти лабиринт.

Задания могут содержать требование: найти са­мый короткий маршрут.

Затем учитель показывает, как выполнить каждое из заданий, отмечая маршруты мелом или маркером. Полезно продемонстрировать, как надо поступить, если сделан ошибочный ход: следует вернуться к развилке и «направиться» по другому маршруту, сменив цвет мела (маркера).

Переменка 1

Игра на развитие памяти «Найдите пару».Игра представляет собой набор из 8-2 пар одина­ковых карточек, которые перед началом игры переме­шивают и «рубашками» вверх раскладывают на столе или крепят на доске рядами.

Учащиеся по очереди «открывают» две любые кар­точки. Если рисунки оказались одинаковые — ученик забирает карточки себе, если разные — карточки сно­ва переворачивают обратной стороной и ход перехо­дит к следующему ученику.

Игра заканчивается, когда все карточки будут ра­зобраны. Победителями становятся ученики, собрав­шие больше карточек.