В декартовой системе координат

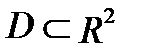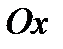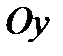О п р е д е л е н и е 3. Замкнутая область называется правильной в направлении оси (оси ), если любая прямая, проходящая через внутреннюю точку области 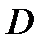и параллельная 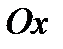оси (оси 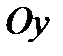), пересекает границу этой области только в двух точках, см. рис. 1 (рис.2).

y y

D D

O x O x

Рис. 1 Рис. 2

З а м е ч а н и е 3. Область, правильная в направлении одной оси, может быть или не быть правильной в направлении другой оси. Например, область на рис. 1 - неправильная в направлении оси 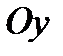(см. рис.3); область на рис.2 - правильная в направлении и оси 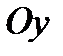, и оси 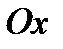(см. рис.4).

y y

O x O x

Рис. 3 Рис. 4

Т е о р е м а 2 (о сведении двойного интеграла к повторному). Пусть замкнутая область 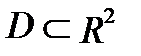ограничена линиями: 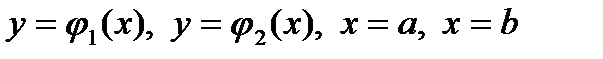, причем на 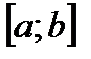функции 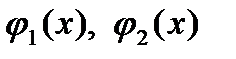непрерывны и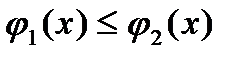 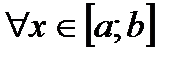(рис. 5). Пусть функция 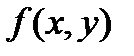непрерывна в замкнутой области 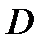. Тогда

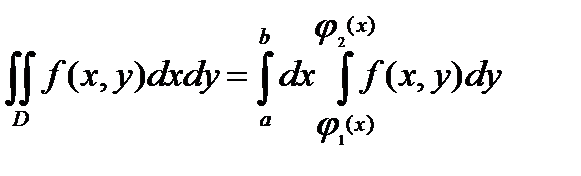. (3)

у

y=j₂ (x)

j₂ (x₀) B

D

j₁ (x₀) y=j₁ (x)

A

O a x₀ b x Рис. 5

Т е о р е м а 3(о сведении двойного интеграла к повторному). Пусть замкнутая область 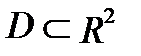ограничена линиями: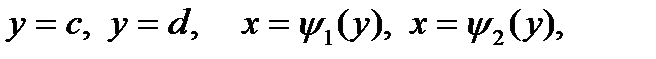

где на 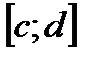функции 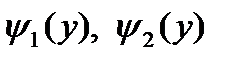непрерывны, причем

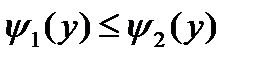
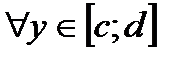(рис. 6).

Пусть функция 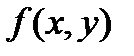непрерывна в области 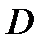. Тогда справедливо равенство:

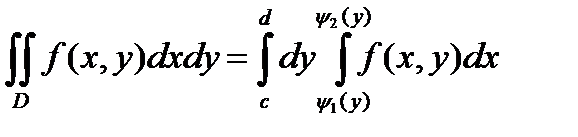. (4)

у

d

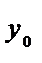А B

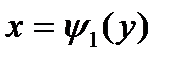
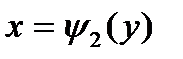
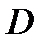
c

О 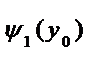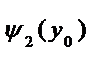х Рис. 6

З а м е ч а н и е 4. Интегралы, стоящие в правых частях формул (3) и (4), называются повторными. Их понимают следующим образом:

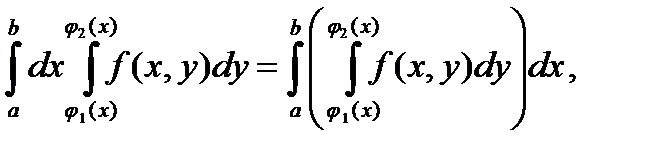
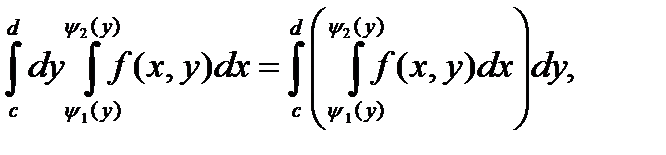
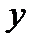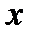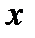где внутренние интегралы вычисляются, соответственно, по при фиксированном (по при фиксированном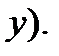

З а м е ч а н и е 5. Если область 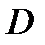является правильной в направлении как оси 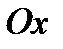, так и оси 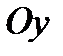, то будем иметь равенства:

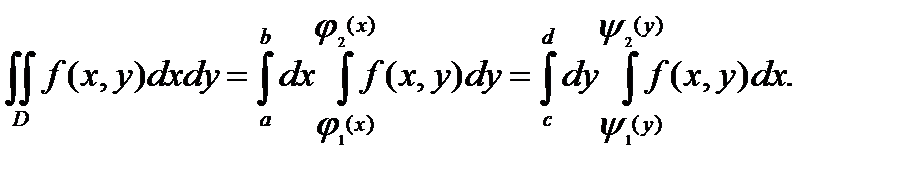
В такой ситуации вычисления можно проводить по любой из формул (3), (4).

З а м е ч а н и е 6. Если область 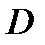не удовлетворяет условиям теорем 2 или 3, то ее следует разбить прямыми, параллельными осям, на части, каждая из которых будет отвечать условиям одной из указанных теорем. Для каждой из образовавшихся областей воспользоваться формулой (3) или (4), полученные результаты сложить на основании свойства 1 двойного интеграла.

П р и м е р 1. Вычислить повторный интеграл

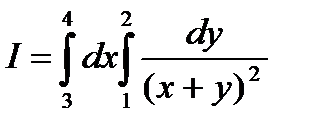(5)

и изобразить область интегрирования.

Р е ш е н и е. Из формулы (5) следует: 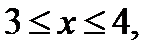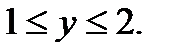Поэтому область интегрирования - прямоугольник, изображенный на рис. 7.

у

2

1

О 3 4 х Рис. 7

Вычислим в (5) внутренний интеграл, считая 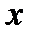постоянной:

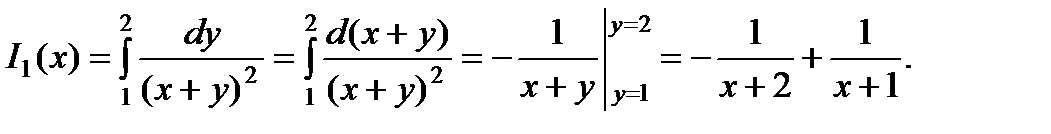
Тогда получаем:

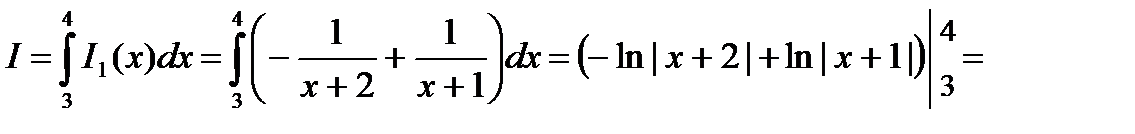
О т в е т: 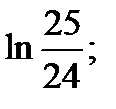рис. 7.

П р и м е р 2.1)Вычислить повторный интеграл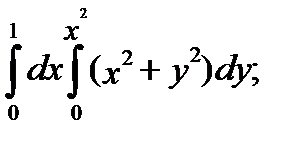

2) Изменить в интеграле порядок интегрирования.

Р е ш е н и е. 1) Предварительно вычислим внутренний интеграл по у при фиксированном х:

.

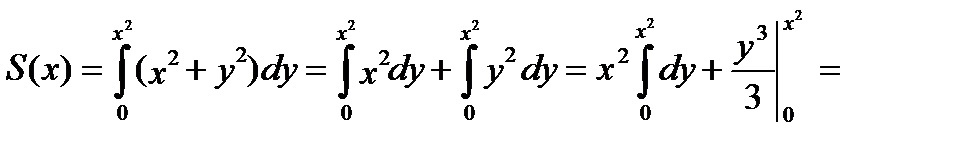
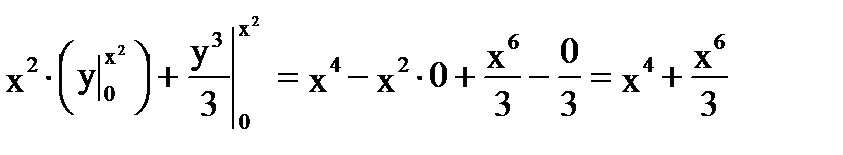Тогда получаем:

.

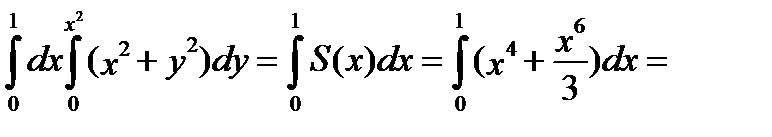
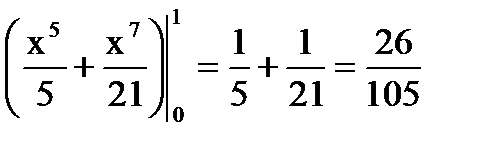2) Область интегрирования 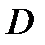является правильной в направлении оси 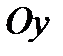и описывается неравенствами 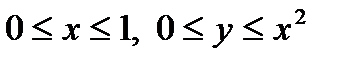, а значит, ограничена линиями 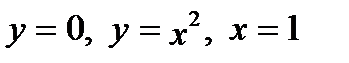и изображена на рис. 8.

Область 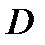является правильной и в направлении оси 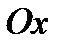. При этом ее можно описать как область на плоскости, удовлетворяющую неравенствам .

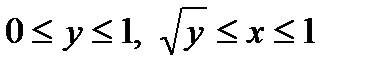у

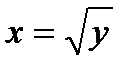
D

O 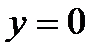1 x Рис. 8

Поэтому из формулы (4) получаем: .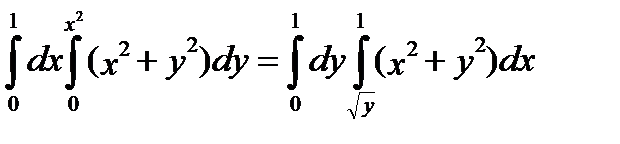

О т в е т: .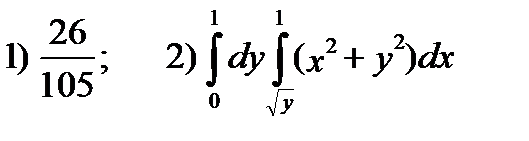

П р и м е р 3. В интеграле 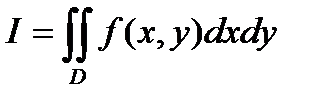расставить пределы интегрирования в одном и другом порядке, если 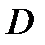- область, ограниченная линиями: .

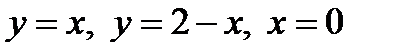Р е ш е н и е. Область 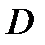изображена на рис. 9. Очевидно, что 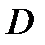- правильная область в направлении оси : .

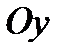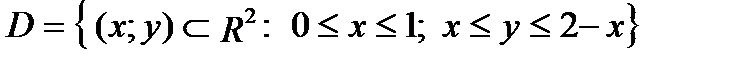у

2

D₂ ^{y = 2- x}

1

D₁

y=x

O 1 x Рис. 9

Поэтому по формуле (3) получим: .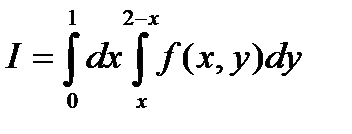

В направлении оси 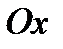правая граница области описывается двумя функциями и не удовлетворяет теореме 3. Однако 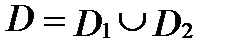, где 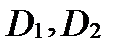- правильные вдоль ос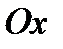и и

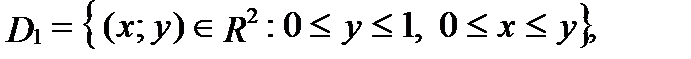
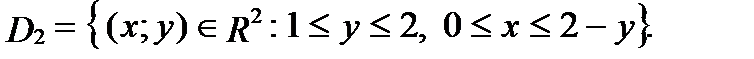
Поэтому по свойству 1 двойного интеграла и формуле (4) получим:

.

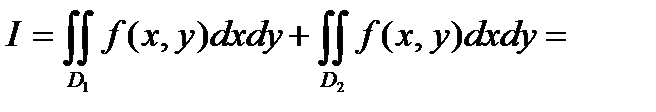
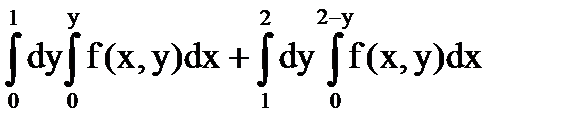О т в е т: .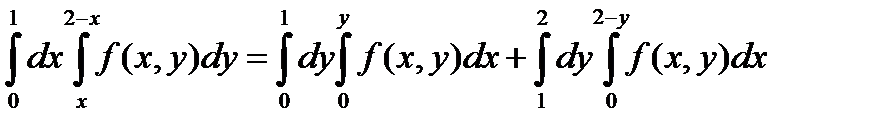

П р и м е р 4. Изменить порядок интегрирования в двойном интеграле

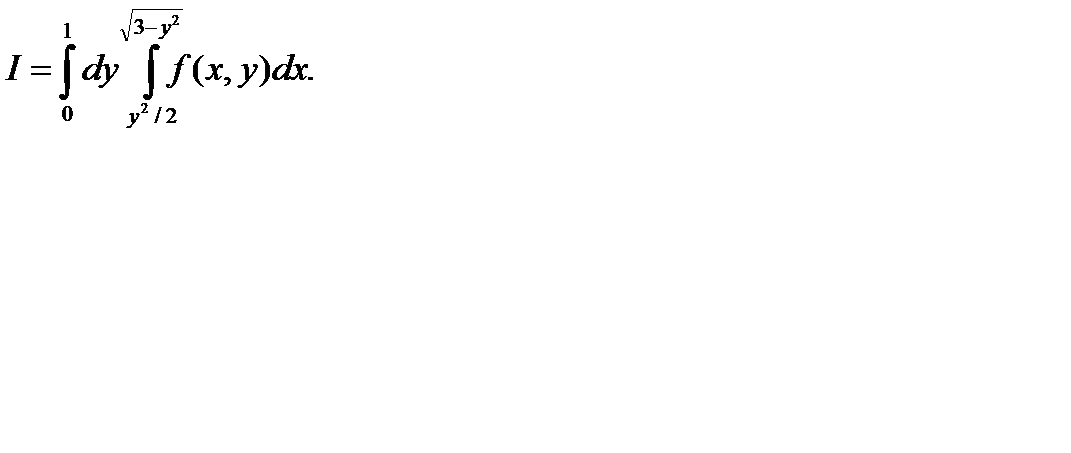
Р е ш е н и е. Изобразим сначала область интегрирования .

По условию примера имеем: (рис. 10).

у

– парабола

– четверть окружности

1

D

О х Рис. 10

Очевидно, что эта область не удовлетворяет условиям теоремы 2. Поэтому, чтобы решить задачу и выполнить интегрирование в другом порядке, предварительно разобьем область на три области с помощью вспомогательных прямых и (рис. 11).

у

1

D₁ D₂ D₃

О 1/2 х Рис. 11

Тогда

Следовательно, получаем:

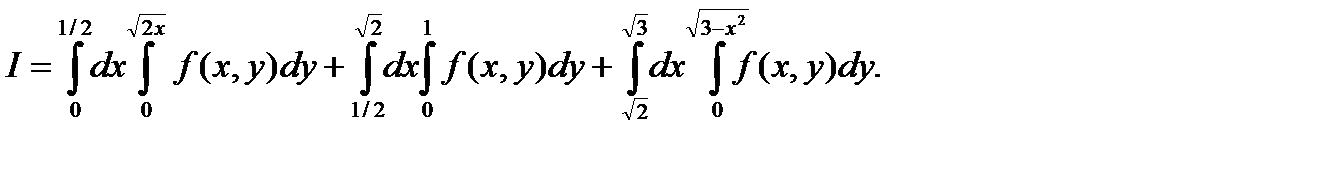
О т в е т: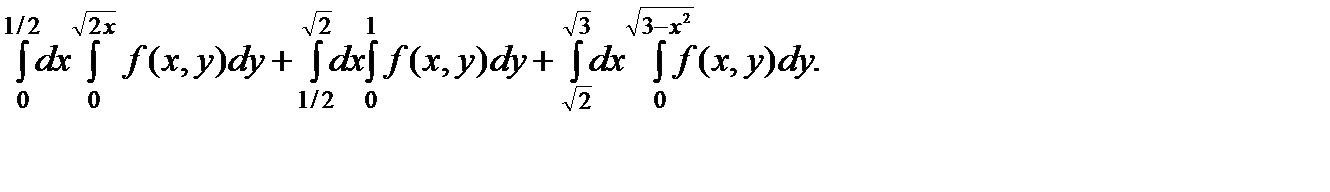

П р и м е р 5. Вычислить двойной интеграл 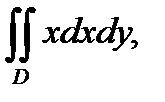где область 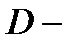треугольник с вершинами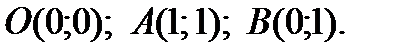

Решение. Построим область интегрирования .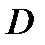

у

1 B A

D

О 1 х Рис. 12

Уравнение прямой 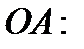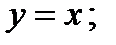прямой 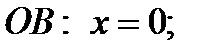прямой 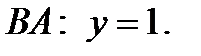При этом 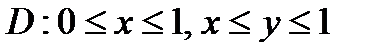(рис. 12). Тогда имеем:

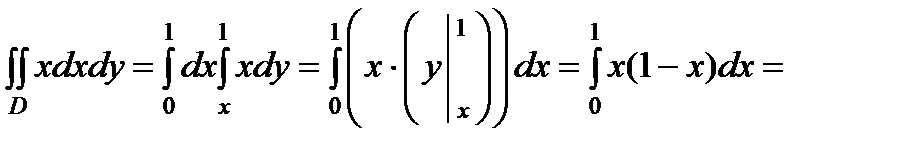
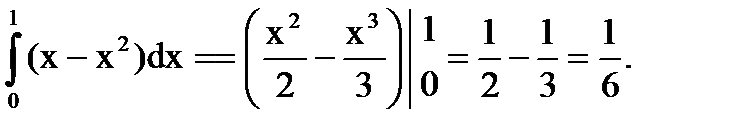
Можно было выполнить интегрирование в другом порядке, рассматривая область :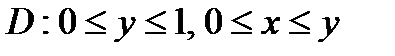

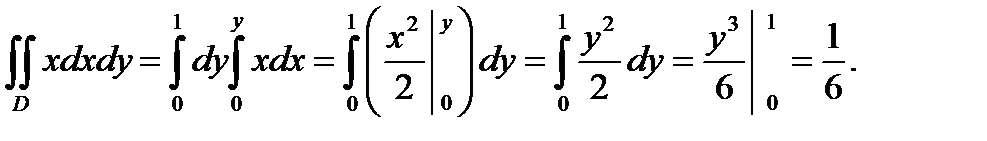
О т в е т: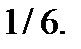

П р и м е р 6. Вычислить двойной интеграл 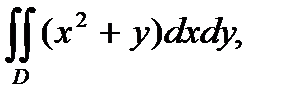если область 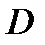ограничена линиями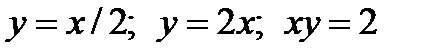

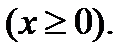
Р е ш е н и е. Построим область 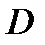(рис. 13).

у

у=2х

2

у=(1/2)х

D₂

D₁ у=2/х

О 12 х

Рис. 13

Для вычисления двойного интеграла необходимо разбить область 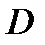на две части прямой 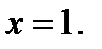Тогда получим:

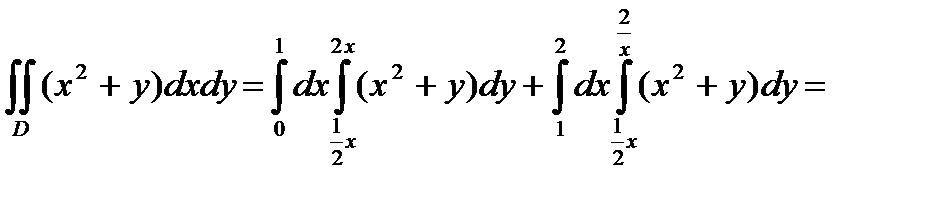
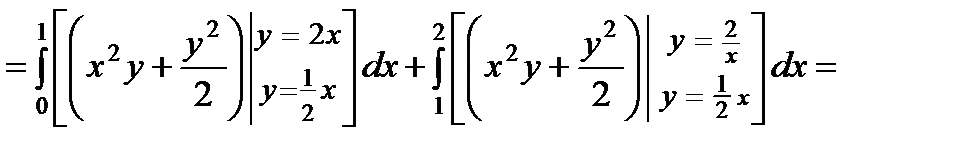
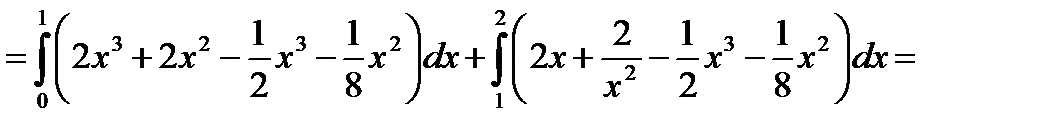
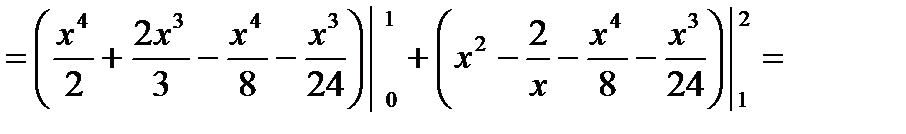
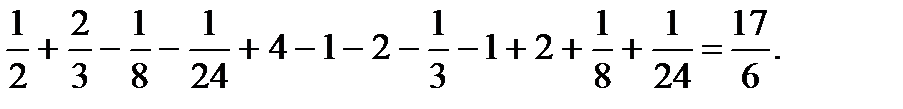
Можно было разбить область 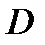на две области прямой 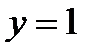(рис. 14).

у х=у/2

2

x=2y

1 D₃

D₄ x=2/y

О 2 х Рис. 14

В этом случае получили бы:

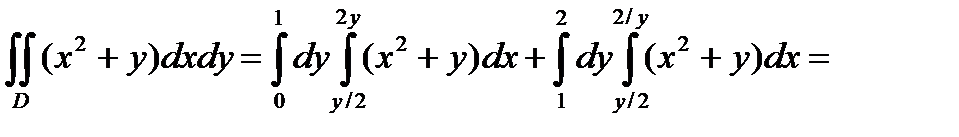
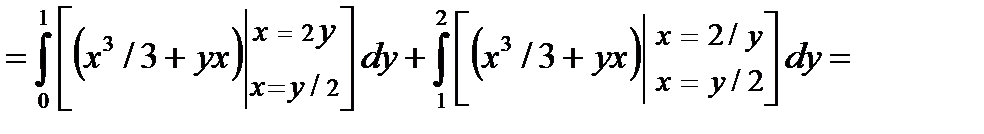
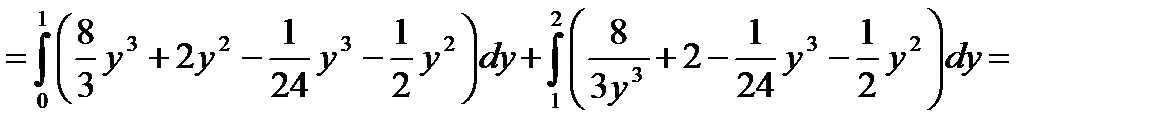
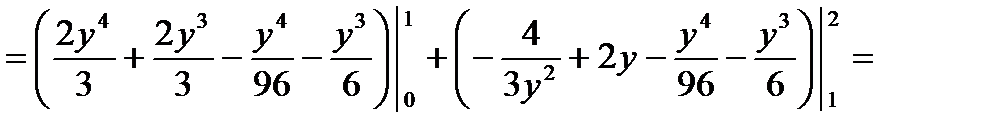
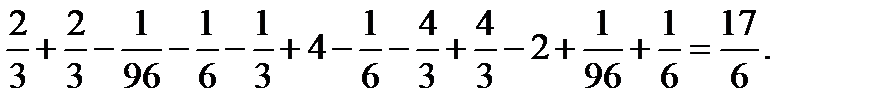
О т в е т: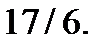

П р и м е р 7. Вычислить 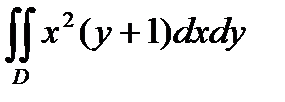, если область 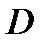ограничена линиями: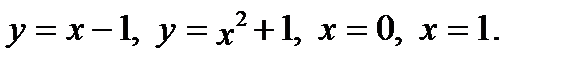

Р е ш е н и е. Область 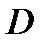изображена на рис. 15.

у

y=x²

1 x=1

O 1 x

y=x-1

-1 Рис. 15

Очевидно, она является правильной вдоль оси 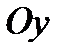и удовлетворяет теореме 2. Поэтому, воспользовавшись формулой (3), получим:

.

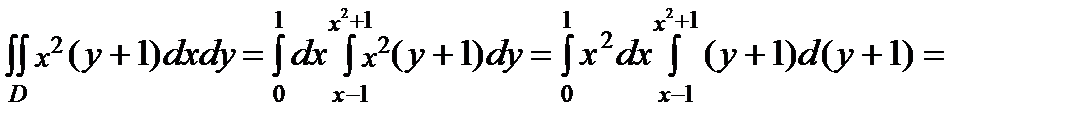
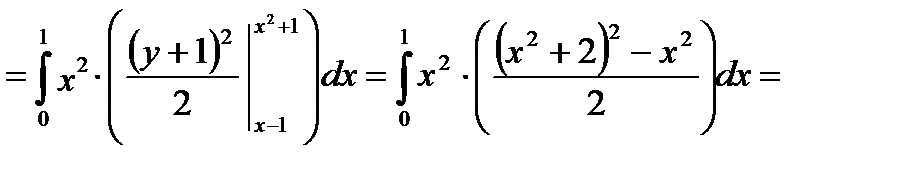
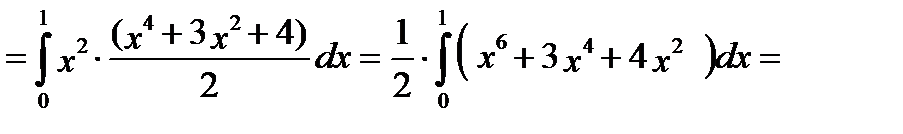
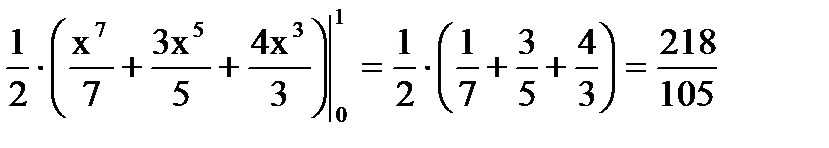О т в е т: