Дифференцирование функции одной
ПЕРЕМЕННОЙ, ЗАДАННОЙ НЕЯВНО
О п р е д е л е н и е 16.Пусть функция 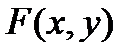 определена на некотором множестве
определена на некотором множестве 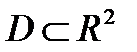 и существует такая функция
и существует такая функция 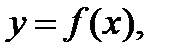 определенная на некотором множестве
определенная на некотором множестве 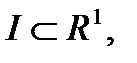 что
что 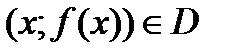
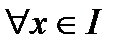 и выполняется равенство:
и выполняется равенство: 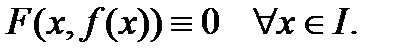 Тогда функция
Тогда функция 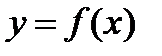 называется неявной функцией, заданной уравнением
называется неявной функцией, заданной уравнением
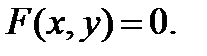 (6)
(6)
Т е о р е м а 6.Пусть функция 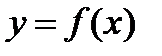 задана неявно уравнением (6), где
задана неявно уравнением (6), где 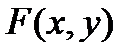 дифференцируема в точке
дифференцируема в точке 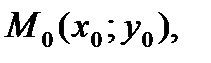 для которой
для которой 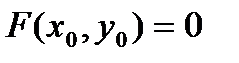 и
и 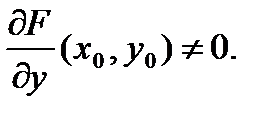 Пусть функция
Пусть функция 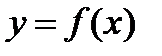 дифференцируема в точке
дифференцируема в точке 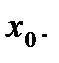 Тогда ее производная в точке
Тогда ее производная в точке 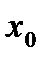 вычисляется по формуле:
вычисляется по формуле: 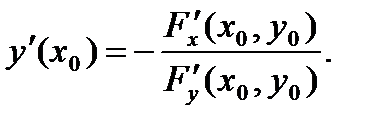
З а м е ч а н и е 10.При выполнении условий теоремы 6 в точке 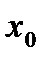 дифференциал функции
дифференциал функции 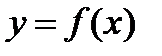 , заданной неявно уравнением (6), вычисляется по формуле:
, заданной неявно уравнением (6), вычисляется по формуле: 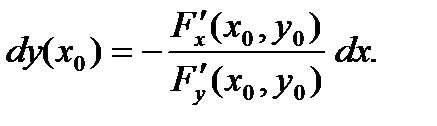
П р и м е р 14. Найти производную функции 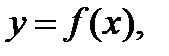 заданной неявно уравнением
заданной неявно уравнением 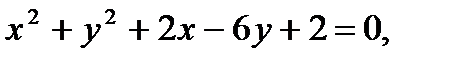 и вычислить ее значение при
и вычислить ее значение при 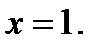
Р е ш е н и е. Обозначив левую часть данного уравнения через 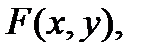 найдем частные производные:
найдем частные производные: 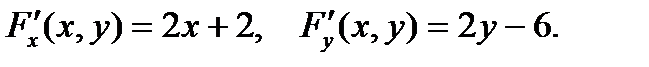 Тогда, воспользовавшись теоремой 6, получаем:
Тогда, воспользовавшись теоремой 6, получаем:
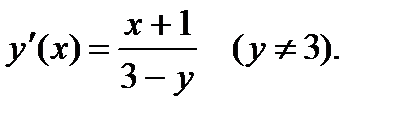 (7)
(7)
Подставим теперь в исходное уравнение 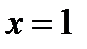 и найдем соответствующие значения функции
и найдем соответствующие значения функции 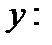
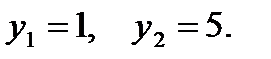 Поэтому по формуле (7) находим:
Поэтому по формуле (7) находим:
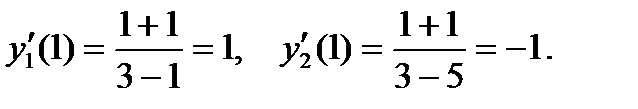
О т в е т: 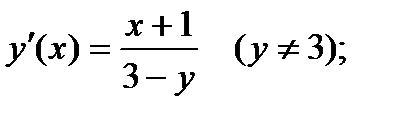
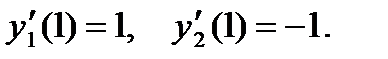
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ДВУХ
ПЕРЕМЕННЫХ, ЗАДАННОЙ НЕЯВНО
О п р е д е л е н и е 17.Если функция 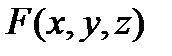 определена на некотором множестве
определена на некотором множестве 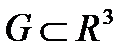 и существует такая функция
и существует такая функция 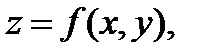 определенная на некотором множестве
определенная на некотором множестве 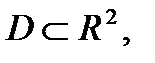 что
что 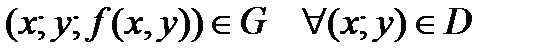 , и выполняется равенство
, и выполняется равенство 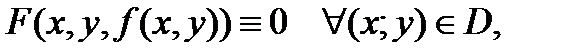 то функция
то функция 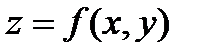 называется неявной функцией, заданной уравнением
называется неявной функцией, заданной уравнением
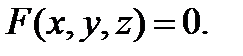 (8)
(8)
Т е о р е м а 7.Пусть функция 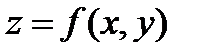 неявно задана уравнением (8), где
неявно задана уравнением (8), где 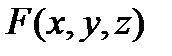 дифференцируема в точке
дифференцируема в точке 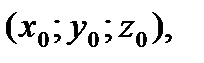 для которой
для которой 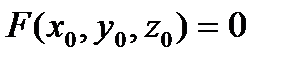 и
и 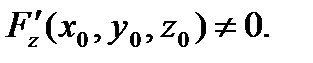 Пусть функция
Пусть функция 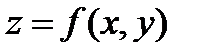 дифференцируема в точке
дифференцируема в точке 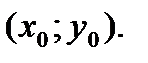 Тогда ее частные производные в точке
Тогда ее частные производные в точке 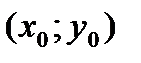 вычисляются по формулам:
вычисляются по формулам:
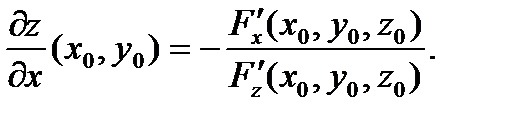
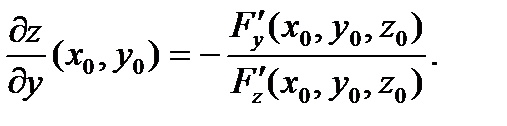 (9)
(9)
З а м е ч а н и е 11.При выполнении условий теоремы 7 в точке 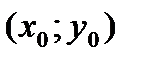 полный дифференциал функции
полный дифференциал функции 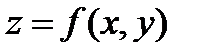 , заданной неявно уравнением (8), вычисляется по формуле:
, заданной неявно уравнением (8), вычисляется по формуле:
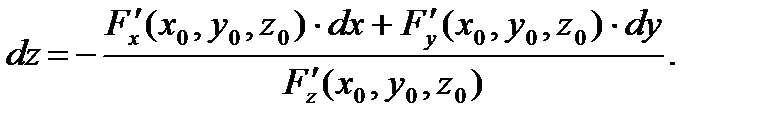
П р и м е р 15. Найти частные производные функции 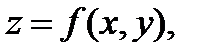 заданной неявно уравнением
заданной неявно уравнением
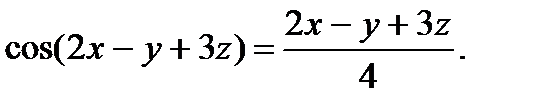
Р е ш е н и е. Рассмотрим функцию:
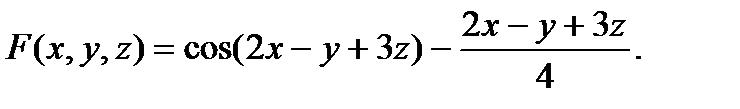 (10)
(10)
Тогда уравнение, заданное в рассматриваемом примере, принимает вид (8). Вычислим частные производные функции (10):
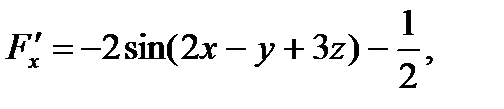
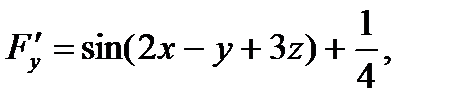
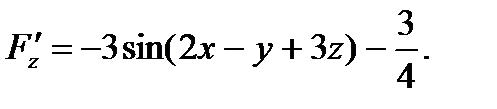
Поэтому, воспользовавшись формулами (9) при условии 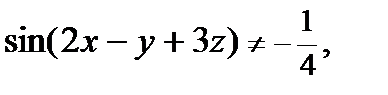 находим:
находим:
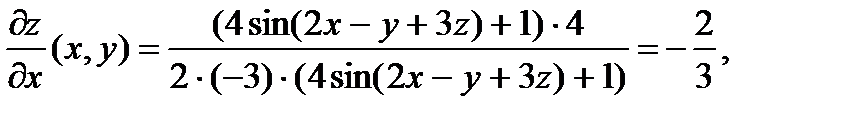
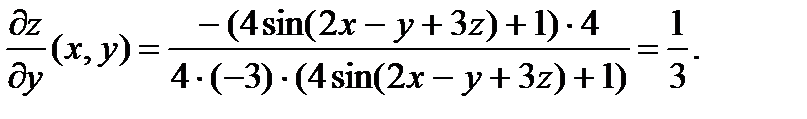
О т в е т: 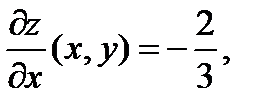
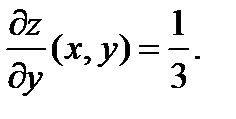
ПРИМЕРЫ
Вычислить пределы функций:
1. 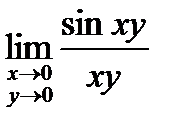 . 2.
. 2. 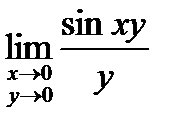 . 3.
. 3. 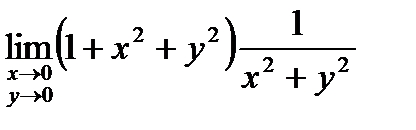 . 4.
. 4. 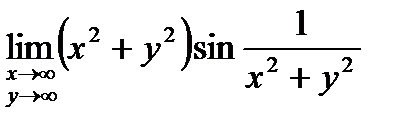 .
.
5. 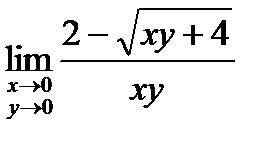 . 6.
. 6. 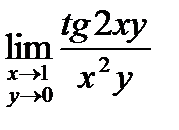 . 7.
. 7. 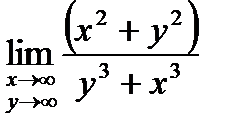 . 8.
. 8. 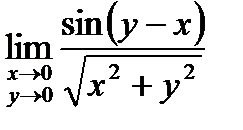 .
.
9. 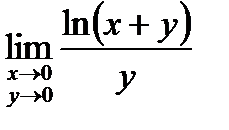 . 10.
. 10. 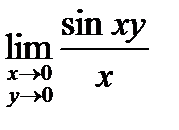 . 11.
. 11. 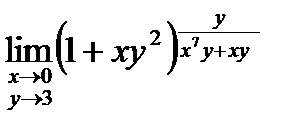 . 12.
. 12. 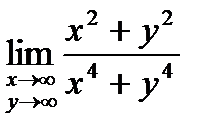 .
.
Найти точки разрыва функции:
13. 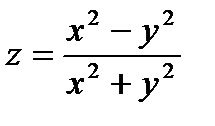 . 14.
. 14. 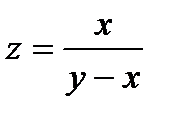 . 15.
. 15. 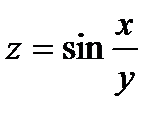 . 16.
. 16. 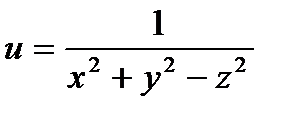 .
.
17. 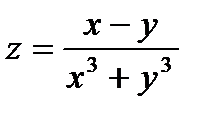 . 18.
. 18. 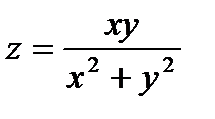 . 19.
. 19. 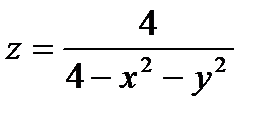 . 20.
. 20. 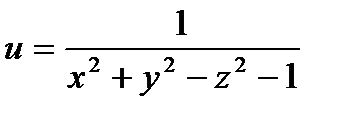 .
.
Найти частные производные функции:
21. 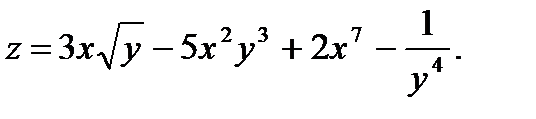 22.
22. 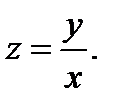 23.
23. 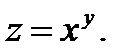 24.
24. 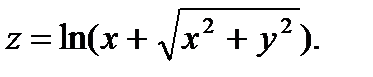 25.
25. 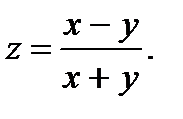
26. 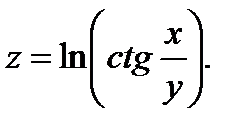 27.
27. 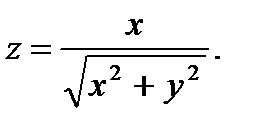 28.
28. 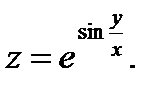 29.
29. 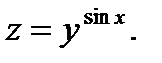 30.
30. 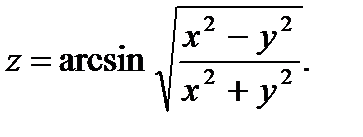
31.Показать, чтодля функции 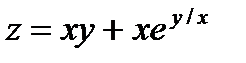 выполняется равенство:
выполняется равенство:
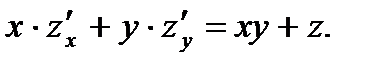
32.Показать, что 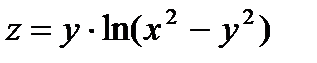 удовлетворяет уравнению:
удовлетворяет уравнению: 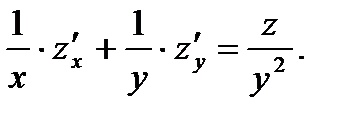
Вычислить значения частных производных функции:
33. 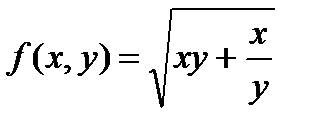 в точке
в точке 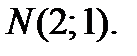 34.
34. 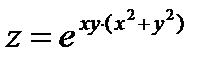 в точке
в точке 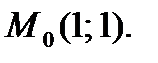
35. 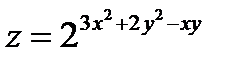 в точке
в точке 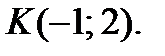 36.
36. 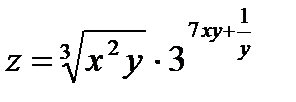 в точке
в точке 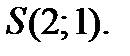
37.Найти частные производные сложной функции 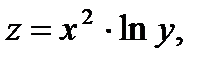 где
где 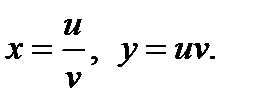
38.Найти производную 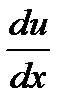 сложной функции
сложной функции 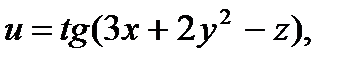 где
где 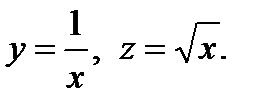
39.Найти 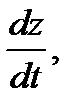 если
если 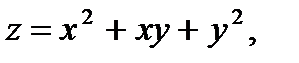 где
где 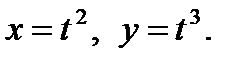
Найти полный дифференциал функции:
40. 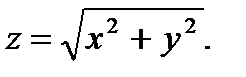 41.
41. 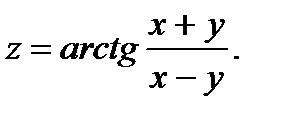 42.
42. 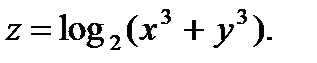
43. 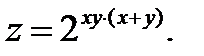 44.
44. 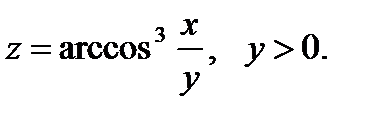 45.
45. 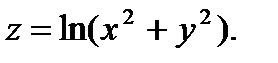 46.
46. 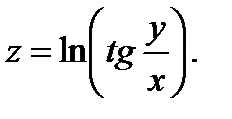
47.Найти значение дифференциала функции 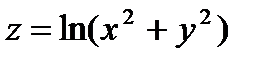 в точке
в точке 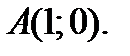
Вычислить приближенно число:
48. 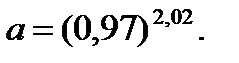 49.
49. 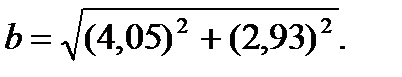 50.
50. 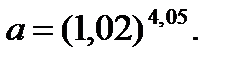
Найти 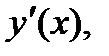 если функция
если функция 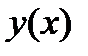 задана неявно уравнением:
задана неявно уравнением:
51. 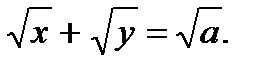 52.
52. 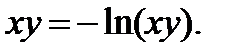 53.
53. 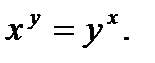 54.
54. 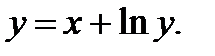 55.
55. 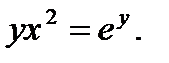
56. 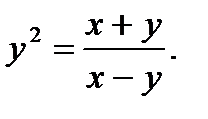 Найти значение производной функции в точке,для которой
Найти значение производной функции в точке,для которой 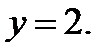
О Т В Е Т Ы
1. 1. 2. 0. 3. е.4. 1. 5. 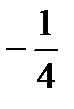 . 6. 2. 7. 0. 8. Не существует.
. 6. 2. 7. 0. 8. Не существует.
9. 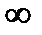 . 10. 0. 11. 3. 12. 0. 13.
. 10. 0. 11. 3. 12. 0. 13. 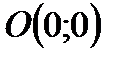 . 14.
. 14. 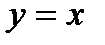 – линия разрыва.
– линия разрыва.
15. 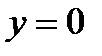 (ось
(ось 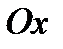 ) – линия разрыва.
) – линия разрыва.
16. 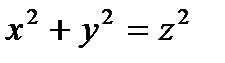 – конус с вершиной в точке
– конус с вершиной в точке 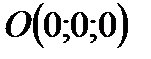 и осью симметрии
и осью симметрии 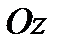 – поверхностью разрыва.
– поверхностью разрыва.
17. 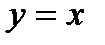 – линия разрыва. 18. Точка
– линия разрыва. 18. Точка 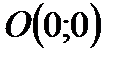 – точка разрыва.
– точка разрыва.
19. 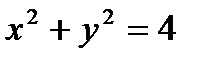 – линия разрыва. 20.
– линия разрыва. 20. 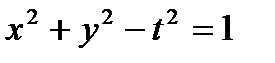 – однополостный гиперболоид с осью симметрии
– однополостный гиперболоид с осью симметрии 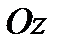 – поверхность разрыва функции.
– поверхность разрыва функции.
21. 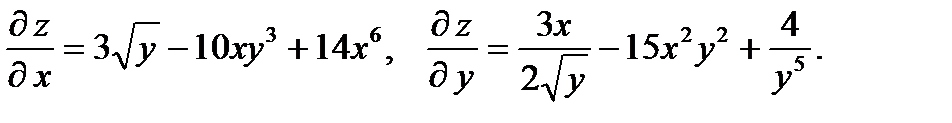 22.
22. 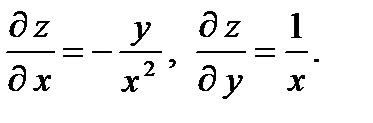
23. 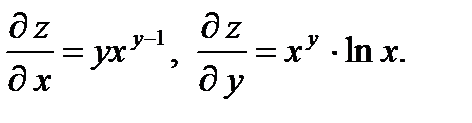 .24.
.24. 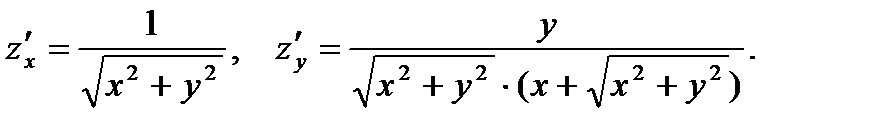
25. 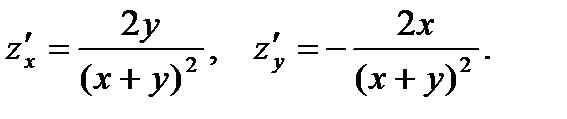 26.
26. 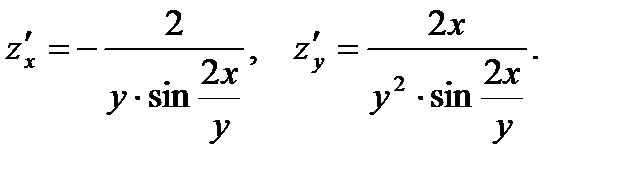
27. 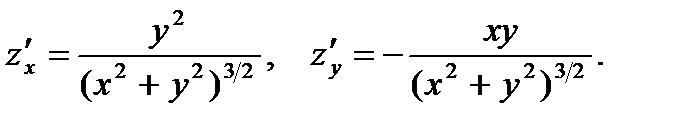 28.
28. 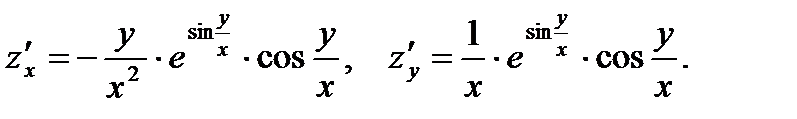
29. 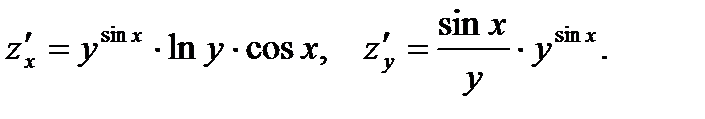 30.
30. 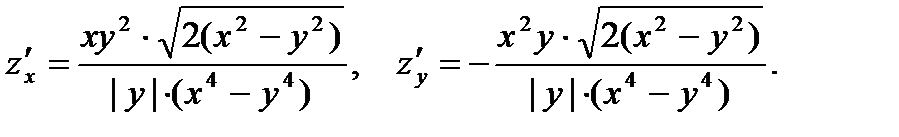
33. 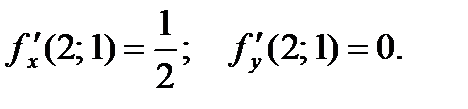 34.
34. 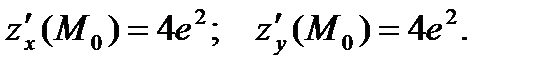
35. 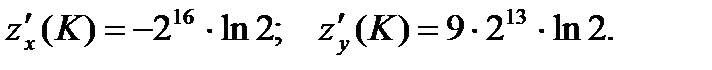 36.
36. 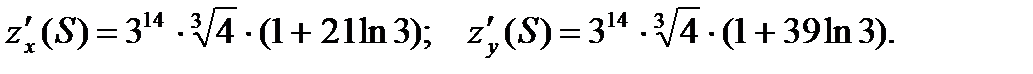
37. 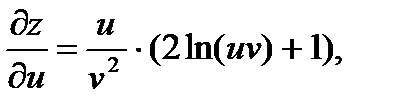
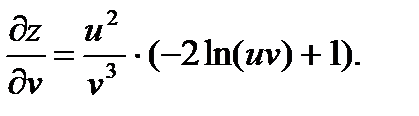
38. 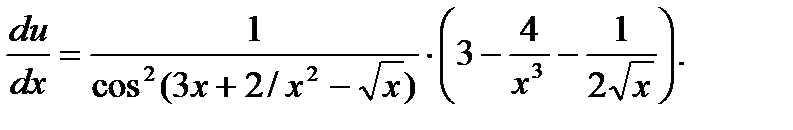 39.
39. 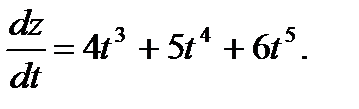
40. 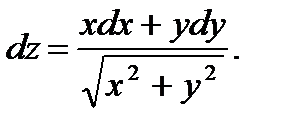 41.
41. 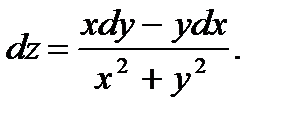 42.
42. 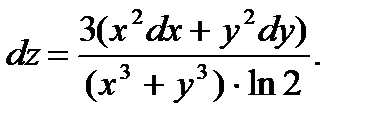
43. 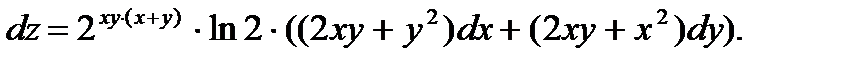
44. 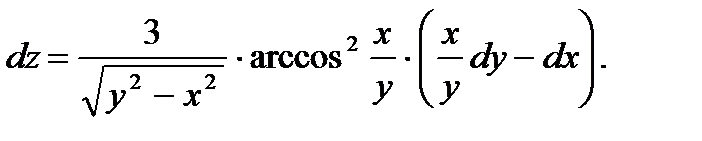 45.
45. 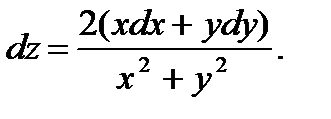 46.
46. 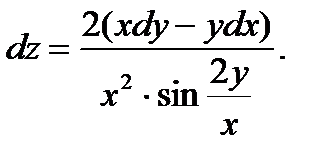
47. 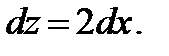 48
48 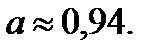 49.
49. 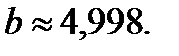 50.
50. 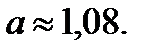 51.
51. 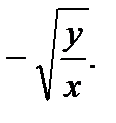 52.
52. 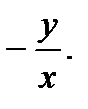
53. 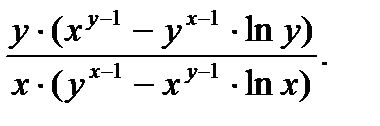 54.
54. 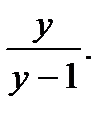 55.
55. 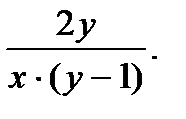
57. 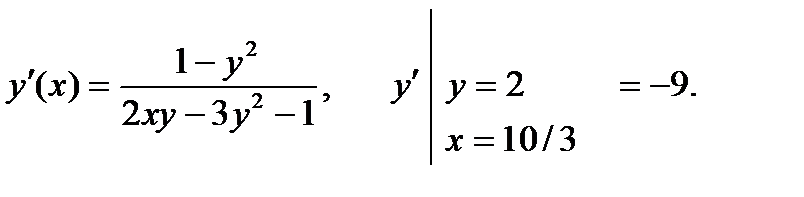
§ 5. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
ВЫСШИХ ПОРЯДКОВ
