Действия с рациональными числами
Методический комментарий
Объяснительный текст пункта подразделяется на три блока: сложение и вычитание рациональных чисел, умножение и деление рациональных чисел, равенство 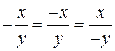 и его применение при вычислениях. Соответствующие блоки есть и в упражнениях к пункту, кроме того, в них добавляется ещё и четвёртый блок — совместные действия с рациональными числами.
и его применение при вычислениях. Соответствующие блоки есть и в упражнениях к пункту, кроме того, в них добавляется ещё и четвёртый блок — совместные действия с рациональными числами.
Вся трудность усвоения действий над рациональными числами состоит в том, что, действуя с целыми числами, ученик оперировал с конкретными количествами, которые мог свободно представить и реально производить операции над ними. Теперь приходится сделать переход к выполнению действий по формальным алгоритмам. Учителю надо иметь в виду, что для некоторых учеников такой переход труден, они долго «цепляются» за содержательные представления и не могут действовать формально. Здесь требуется индивидуальный подход, в частности привлечение материалов, аналогичных заданиям из дидактических материалов.
При выполнении заданий на вычисление суммы (произведения, частного) двух чисел учащиеся должны последовательно отвечать на вопросы: какой знак имеет сумма (произведение, частное)? Как найти модуль суммы (произведения, частного)?
Не следует спешить с использованием различных возможностей для вычислений, в частности, рассмотренной в учебнике на с. 240, где равенство 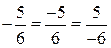 позволяет показать третью запись для примера 1, а именно:
позволяет показать третью запись для примера 1, а именно: 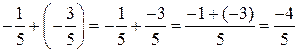 .
.
Комментарий к упражнениям
915. По ходу вычислений можно ставить вопросы: какое слагаемое имеет больший модуль? Какой знак имеет это слагаемое? Какой знак имеет сумма? Как найти модуль суммы, модули слагаемых?
920, 921. Отрабатываются различные случаи вычитания отрицательного и положительного чисел.
924. Надо напоминать учащимся, что любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как сумму. Упрощение вычисления значения выражения (вычисление отдельно суммы положительных слагаемых и отрицательных слагаемых) основывается на применении законов сложения.
940—942. Упражнения необходимо дополнить упражнениями на совместные действия из дидактических материалов.
954. Полезен вывод: чётная степень отрицательного числа — положительное число, нечётная степень отрицательного числа — отрицательное число.
958. 1) Вывод: если в данном выражении изменить знак перед каждым числом на противоположный, то получится выражение, значение которого противоположно значению данного выражения.
2) а) – (–15 + 8) = 15 – 8.
Что такое координаты
Методический комментарий
Основная цель — познакомить учащихся с идеей системы координат, привлекая доступные для их понимания примеры. В дополнение к упражнениям учебника можно выполнить практическую работу по туристической схеме какого-нибудь города. На листе со схемой обычно приводится список достопримечательностей с указанием места расположения каждой из них (в виде записи координат квадрата, в котором отмечена достопримечательность). Учитель может предложить по указанным координатам найти ту или иную достопримечательность на карте, а также отметить место расположения школы (почты, стадиона и т. д.) и определить её координаты.
Комментарий к упражнениям
969. Для упражнения понадобятся транспортир и линейка.
Маршрут: палатка, 50°, 80 м; озеро, 0°,120 м; луг, 65°, 60 м; сухое дерево, 50°, 90 м; белый камень, 35°, 170 м.
