Свойства сложения и умножения
Методический комментарий
Начиная рассмотрение переместительного и сочетательного свойств сложения и умножения, полезно подчеркнуть, что они не только хорошо известны учащимся, но и постоянно используются в вычислениях. Так, вычисляя устно сумму 36 + 14, мы фактически находим значение выражения 36 + (4 + 10), которое подсчитывается в два этапа: 36 + 4 = 40 и 40 + 10 = 50. Иными словами, мы пользуемся сочетательным свойством, выражающим правило прибавления к числу суммы: 36 + (4 + 10) = (36 + 4) + 10.
Другой пример. В таблице умножения в столбике, где приводятся результаты умножения на 3, есть равенство 5 · 3 = 15. Однако в столбце, где даны результаты умножения на 5, нет произведения 3 · 5. И это естественно, так как 3 · 5 = 5 · 3.
В учебнике даются следствия из переместительного и сочетательного свойств — обобщённые правила, согласно которым компоненты суммы и произведения можно произвольным образом переставлять и объединять в группы. Эти правила служат практической основой выполнения преобразований числовых выражений. Их формулировки учащиеся должны выучить наизусть.
Чтобы учащиеся лучше усвоили правила, можно предлагать упражнения такого типа:
1) Запишите разными способами, используя скобки, сумму чисел 57, 49 и 43. Какой из способов удобнее для вычисления?
2) Запишите разными способами произведение чисел 4, 31 и 25. В каком случае легче подсчитать значение произведения?
Учащиеся должны понять, что, применяя свойства, мы изменяем порядок выполнения действий, и в результате этого могут упроститься вычисления. Так, в сумме удобно группировать те слагаемые, при сложении которых получается круглое число. Точно так же в произведении целесообразно объединять в группы те числа, при умножении которых получается число, оканчивающееся нулём. Можно записать в тетрадях и предложить запомнить такую таблицу:
5 · 2 = 10,
25 · 4 = 100,
125 · 8 = 1000.
Зная её, несложно, например, вычислить устно произведение 125 · 25 · 8 · 4.
Упражнения данного пункта предполагают применение рациональных приёмов вычислений. В связи с этим необходимо заметить, что умение считать рационально может рассматриваться лишь как желаемый результат изучения данной темы. Обязательным для всех требованием остаётся получение правильного ответа. А выбор способа вычисления — это право ученика.
Комментарий к упражнениям
312. Слагаемые, дающие в сумме круглое число, можно соединить дугами. Переписывать выражения, заключая эти слагаемые в скобки, необязательно.
315. Идея решения раскрывается в примере 3 объяснительного текста, который надо предварительно разобрать.
а) 36 · 25 = 9 · 4 · 25 = 9 · 100 = 900;
б) 125 · 12 = 5 · 25 · 4 · 3 = 15 · 100 = 1500;
в) 75 · 24 = 3 · 25 · 4 · 6 = 18 · 100 = 1800;
г) 150 · 42 = 150 · 6 · 7 = 900 · 7 = 6300.
В упражнениях 320, 321 используется приём замены числа произведением чисел и обратное преобразование.
320. а) 75 · 14 · 18 = (25 · 3) · (2 · 7) · (2 · 9) =
= (25 · 4) · (3 · 7 · 9) = 18 900;
б) 16 · 125 · 4 · 35 = (2 · 35) · (125 · 8) · 4 =
= 70 · 1000 · 4 = 280 000.
321. г) 182 · 66 = 2 · 7 · 13 · 2 · 3 · 11 = (7 · 11 · 13) · (2 · 2 · 3) =
= 1001 · 12=12 012.
322. Надо убедиться, что учащиеся понимают, что означает многоточие в записи суммы.
а) Так как это первый пример, то полезно сначала записать сумму полностью, сосчитать число слагаемых, соединить дугами пары чисел, дающих в сумме одно и то же число, выяснить, сколько таких пар.
б) Вначале полезно записать данную сумму, указав в ней явно несколько последних слагаемых:
5 + 10 + 15 + 20 + ... + 85 + 90 + 95 + 100.
Теперь учащимся легче будет увидеть пары чисел, дающих в сумме одно и то же число 105. Всего таких пар 10.
323. а) Легко понять закономерность: 1 + 3 + 5 + 7 = 42, 1 + 3 + 5 + 7 + 9 = = 52 и т. д. В сумме 1 + 3 + 5 + ... + 99 содержится 50 слагаемых, поэтому она равна 502.
Распределительное свойство
Методический комментарий
Данный вопрос, как правило, вызывает определённые трудности у учащихся. Особенно это относится к применению распределительного свойства для обратного преобразования — вынесения множителя за скобки. Поэтому на данном этапе никаких обязательных требований к усвоению этого материала не предъявляется. Основное его назначение — это приобретение некоторого опыта преобразования числовых выражений на основе распределительного свойства.
Изложение материала в учебнике начинается с рассмотрения уже знакомой учащимся задачи вычисления площади прямоугольника, составленного из двух прямоугольников одинаковой ширины. По условию задачи составляются два различных выражения, значения которых равны. Записывается равенство (5 + 3) · 4 = 5 · 4 + 3 · 4. В его левой части — произведение, в правой — сумма. Это равенство можно прочитать словами: произведение суммы 5 + 3 и числа 4 равно сумме произведений 5 · 4 и 3 · 4. Аналогичные равенства можно составить и прочитать при работе с другими задачами, предложенными в учебнике. Затем распределительное свойство формулируется и записывается с помощью букв. Учащимся сообщается, что обычно распределительное свойство читается как правило умножения суммы на число и что оно справедливо для суммы любого числа слагаемых.
Закрепляется рассмотренный материал заданиями из учебника к этому фрагменту (с. 86). Далее обращается внимание на то, что вычитание вместе с умножением также обладает распределительным свойством, и выполняются упражнения 327—329. В упражнениях 330, 331 выражение со скобками преобразуется путём применения распределительного свойства и теперь его можно сравнить с другим данным выражением без скобок.
Следующий шаг в изучении данного вопроса — это применение распределительного свойства для преобразования суммы в произведение. Объяснение можно провести, рассмотрев те задачи, при решении которых вводилось распределительное свойство. Только теперь равенство, записанное, например, по условию задачи на нахождение площади прямоугольника, должно выглядеть так: 5 · 4 + 3 · 4 = (5 + 3) · 4.
В результате мы придём к преобразованию суммы в произведение, которое называется вынесением общего множителя за скобки.
Для выработки умения выполнять это преобразование в прямом, неосложнённом случае можно использовать упражнение 332. Общие множители обязательно нужно каким-либо способом выделять — подчёркивать, обводить кружком и т. д. Кроме того, нужно приучить учащихся для контроля устно выполнять обратное преобразование: если получилось исходное выражение, то вынесение множителя за скобки выполнено верно.
В учебнике и в дидактических материалах есть ряд трудных упражнений (задания 337 и 338 из учебника). Их целесообразно использовать в работе с сильными учащимися. Заметим, что в заданиях такого рода возможны разные решения. Так, в примере 2 из теоретической части пункта преобразования можно было бы выполнить иначе:
46 · 32 + 8 · 16 = 46 · 32 + 4 · 32 = (46 + 4) · 32 = 50 · 32 = 1600.
Приведём несколько дополнительных заданий, предполагающих рациональные способы вычислений:
1) 48 · 32 + 48 · 68 + 52 · 37 + 52 · 63;
2) 39 · 73 + 39 · 27 + 61 · 15 + 85 · 61;
3) (125 + 87) · 8 + 87 · 2;
4) (317 + 25) · 4 – 3 · 317.
Комментарий к упражнениям
335, 336. Разбираются полезные приёмы умножения на 15, на 101. Желательно их рассмотреть в любом классе. В классе с хорошей математической подготовкой предложите учащимся объяснить приёмы умножения на 1001, на 111, на 99.
337. Используются приёмы умножения на 11, на 15.
а) 22 · 26 – 11 · 26 = 26 · 11 = 260 + 26 = 286;
г) 48 · 11 + 48 · 4 = 48 · 15 = 480 + 240 = 720.
338. а) 12 · 17 + 17 · 23 + 35 · 13 = (12 + 23) · 17 + 35 · 13 =
=35 · 17 + 35 · 13 = 35 · 30 = 1050;
Задачи на части
Методический комментарий
Задачи на части, а в следующем пункте и задачи на уравнивание продолжают линию решения текстовых задач арифметическим способом. Не следует стараться обязательно решить сразу все предлагаемые в этих пунктах задачи. Времени может оказаться недостаточно, а спешка повредит конечной цели — развитию мышления, овладению приёмами рассуждений.
Объяснение можно начать с задачи 1 из учебного текста.
Решение задачи можно записать с вопросами:
1) Сколько килограммов ягод приходится на 1 часть?
9 : 3 = 3 (кг).
2) Сколько килограммов сахара надо взять?
3 · 2 = 6 (кг).
Ответ. 6 кг.
Вначале решаются задачи, в которых о частях говорится в явном виде (342, 343). Заметим, что в условии задачи даётся масса не одного из компонентов, а всей смеси, сплава и т. д.
После этого решаются задачи, в которых известно, на сколько масса одной составляющей смеси больше массы другой составляющей (задача 345). И затем, после рассмотрения задачи 2 из учебного текста, решаются задачи, в которых части в явном виде не указаны, а говорится лишь, во сколько раз одна величина больше или меньше другой (347, 348 и др.).
Комментарий к упражнениям
Условия задач необходимо иллюстрировать схематическими рисунками, которые позволяют проводить рассуждения на наглядной основе. Без рисунков этот тип задач многим учащимся окажется просто непосильным.
345. По условию задачи делается рисунок (рис. 4,8 в учебнике), на котором надо отметить отрезок, изображающий 36 ц. Теперь можно решать задачу: 36 ц составляют 2 части, значит, на одну часть приходится 36 : 2 = = 18 (ц); ржи смололи 18 · 4 = 72 (ц).
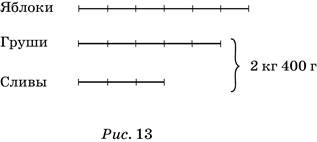
346.Выделяется подзадача: взяли 5 частей груш и 3 части слив, что составило вместе 2 кг 400 г (рис 13).
349. а) Задачу нужно переформулировать: мальчик сорвал орехов в 2 раза больше, чем девочка.
350. а) После явного введения частей и выполнения рисунка задача становится такой же, как задача 345.
351. а) Сначала надо «исключить» третий день, т. е. узнать, сколько страниц Митя прочитал за два дня. После этого получается уже хорошо знакомая задача на части, которая решается с опорой на рисунок.
б) «Исключив» первый кусок ткани, получаем задачу: «Кусок ткани длиной 51 м разрезан на две части, одна из которых в 2 раза короче другой. Какова длина каждой части?»
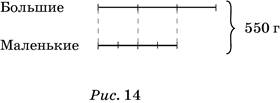
352. Решение понятно из рисунка 14.
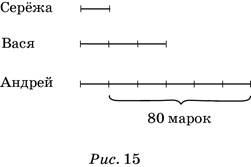
354. Сначала переформулируем условие так: «У Васи в 3 раза больше марок, чем у Серёжи, а у Андрея — в 2 раза больше марок, чем у Васи». Это условие изображаем в виде схемы (рис. 15), причём начинаем с изображения количества марок у Серёжи (это одна часть). Далее на рисунке нужно найти отрезок, составляющий 80 марок.
Задачи на уравнивание
Методический комментарий
Здесь рассматриваются задачи указанного вида, в которых известны сумма двух величин и их разность. Более сложные задачи на уравнивание разбираются в курсе 6 класса.
Для того чтобы облегчить учащимся овладение самой идеей уравнивания, целесообразно организовать реальную деятельность по уравниванию величин, рассматриваемых в условии задачи.
Так, если объяснение проводить на задаче, разобранной в учебнике, то нужно положить на стол две пачки тетрадей и затем сообщить учащимся условие задачи. Задача решается устно, причём решение сопровождается реальными действиями с тетрадями. После этого решение можно записать на доске с комментарием. Запись может быть такой:
1) 70 – 10 = 60 (тетр.) — столько тетрадей будет в двух пачках, если убрать 10 тетрадей;
2) 60 : 2 = 30 (тетр.) — столько тетрадей во второй пачке;
3) 30 + 10 = 40 (тетр.) — столько тетрадей в первой пачке.
Эту же задачу целесообразно решать иначе, предложив другие приёмы уравнивания тетрадей в пачке. (Каждый из рассматриваемых способов также должен сопровождаться реальными действиями с тетрадями.) Так, можно уравнять пачки, добавив во вторую 10 тетрадей, а можно уравнять число тетрадей в пачках, переложив половину разницы (5 тетрадей) во вторую пачку. При любом способе решения учащиеся должны привыкнуть для самоконтроля проводить проверку (см. текст учебника). Она может выполняться устно. Таким же способом учитель должен опровергать неверные решения.
Вначале решаются задачи 359—361. Решение одной из более сложных задач на уравнивание (задача 362) сначала разбирается фронтально по учебнику, а затем две похожие задачи предлагаются учащимся для решения рассмотренным способом. Задачи 364—368 — трудные, в слабом классе их лучше не рассматривать.
Комментарий к упражнениям
359—361. Решение первых задач полезно проводить с привлечением каких-либо реальных предметов (необязательно тех, о которых идёт речь в задаче, например, спичек). Затем можно перейти к схематическим рисункам, где величины, о которых идёт речь в задаче, изображаются отрезками.
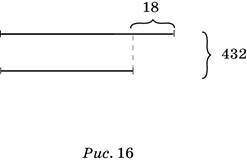
363. а) Пусть оба числа равны меньшему из них, тогда их сумма будет 432 – 18 = 414 (рис. 16). Меньшее число равно 414 : 2 = 207, а большее число равно 207 + 18 = 225. (Задачу полезно решить и другим способом.)
364. Задача существенно сложнее предыдущей, так как вместо уже привычной ситуации — «одно число больше (меньше) другого на ...» — дана разность чисел. Итогом решения этой задачи может быть, вообще говоря, такой вывод: чтобы найти два числа по их сумме и разности, можно из суммы вычесть разность; в результате получится удвоенное меньшее число. Конечно, это следует делать только в хорошо подготовленном классе.
366. а) Последовательные натуральные числа отличаются друг от друга на единицу. Условие задачи можно проиллюстрировать с помощью
рисунка 17.
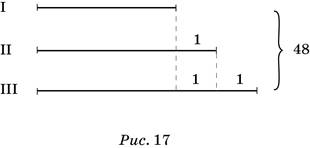
Решение может быть таким: будем считать, что слагаемые равны меньшему числу, тогда их сумма будет 48 – 3 = 45; меньшее число равно
45 : 3 = 15, а два других — это 15 + 1 = 16 и 16 + 1 = 17. (Проверьте: числа 15, 16 и 17 — это последовательные натуральные числа и 15 + 16 + 17 = 48.)
368. Если бы отцу было столько же лет, сколько матери, то сумма возрастов была бы равна 103 – 5 = 98 годам.
Далее имеем задачу на части. Здесь удобно возраст матери принять за 20 частей, тогда на возраст сына приходится 20 : 4 = 5 частей, а на возраст дочери — 20 : 5 = 4 части.
Запись решения:
1) 20 + 20 + 5 + 4 = 49 — столько частей приходится на суммарный возраст;
2) 98 : 49 = 2 — столько лет приходится на 1 часть;
3) 2 · 20 = 40 — столько лет матери;
4) 40 + 5 = 45 — столько лет отцу;
5) 2 · 5 = 10 — столько лет сыну;
6) 2 · 4 = 8 — столько лет дочери.
Глава 5. Углы и многоугольники (9 уроков)
Примерное поурочное планирование учебного материала
| Пункт учебника | Число уроков | Рабочая тетрадь, номер задания | Характеристика деятельности учащихся |
| 5.1. Как обозначают и сравнивают углы | 43—48 (ч. 2) | Распознавать на чертежах, рисунках и моделях углы. Распознавать прямой, развёрнутый, острый, тупой углы. Изображать углы от руки и с использованием чертёжных инструментов на нелинованной и клетчатой бумаге, моделировать из бумаги и других материалов. Распознавать, моделировать биссектрису угла | |
| 5.2. Измерение углов | 49—62 (ч. 2) | Распознаватьна чертежах, рисунках и моделях прямые, острые, тупые и развёрнутые углы. Измерятьс помощью транспортира и сравниватьвеличины углов. Строитьуглы заданной величины с помощью транспортира. Решатьзадачи на нахождение градусной меры углов | |
| 5.3. Ломаные и многоугольники | 63—73 (ч. 2) | Распознавать многоугольники на чертежах, рисунках, находить их аналоги в окружающем мире. Моделировать многоугольники, используя бумагу, проволоку и т. д., изображатьна нелинованной и клетчатой бумаге. Измерятьдлины сторон и величины углов многоугольников. Проводить диагонали многоугольников. Использовать терминологию,связанную с многоугольниками. Конструировать алгоритм воспроизведения рисунков, построенных из многоугольников, строить по алгоритму, осуществлять самоконтроль, проверяя соответствие полученного изображения заданному рисунку. Вычислять периметры многоугольников | |
| Обзор и контроль | Моделировать многоугольники, используя бумагу, проволоку и т. д., изображатьна нелинованной и клетчатой бумаге.Распознавать прямые, острые, тупые углы многоугольников. Измерятьдлины сторон и величины углов многоугольников. Изображатьмногоугольники. Разбивать многоугольник и составлятьмногоугольник из заданных многоугольников. Определять число диагоналей многоугольника. Использовать терминологию,связанную с многоугольниками. Конструировать алгоритм воспроизведения рисунков, построенных из многоугольников, строить по алгоритму, осуществлять самоконтроль, проверяя соответствие полученного изображения заданному рисунку.Выдвигать гипотезы о свойствах многоугольников и обосновывать их. Вычислять периметры многоугольников |
Основные цели: познакомить учащихся с новой геометрической фигурой — углом; ввести понятие биссектрисы угла; научить распознавать острые, тупые и прямые углы, строить и измерять углы с помощью транспортира, оценивать величину угла на глаз; развить представление о многоугольнике.
Обзор главы.Материал данной главы содержит два смысловых блока.
Первый из них связан с введением новой для учащихся геометрической фигуры, которой является угол, и связанных с ней понятий (виды углов, измерение углов). Учащиеся учатся изображать углы, обозначать их, распознавать в различных положениях. Одним из важнейших умений, которым они должны овладеть на этой стадии обучения, является сравнение углов. Формируется это умение на основе практического действия — наложения углов друг на друга. Классификация углов проводится через сравнение с наиболее часто встречающимся в окружающем мире прямым углом: угол, меньший прямого, является острым, больший прямого, — тупым. Измерение углов является для учащихся новым видом измерений, который знакомит их с угловой мерой и новым измерительным прибором — транспортиром.
Второй блок содержания связан с многоугольниками и содержит материал, частично знакомый учащимся из начальной школы. Теперь им предстоит расширить свои представления об уже знакомых фигурах, усвоить связанную с ними терминологию (вершина, сторона, угол многоугольника, диагональ), научиться «видеть» их в более сложных конфигурациях. Отрезок и угол здесь — элементы многоугольника. Учащиеся учатся изображать многоугольники с заданными свойствами на нелинованной и клетчатой бумаге, обозначать их, находить периметр.
Заметим, что в учебнике мы рассматриваем углы, меньшие развёрнутого. Однако угол многоугольника может быть и больше развёрнутого (невыпуклые многоугольники). Внимание учащихся на этом не акцентируется, так как невыпуклые многоугольники встречаются на рисунках лишь для создания более полного представления о многоугольниках, но никакая практическая работа с ними не проводится.
Материалы для контроля.
Пособие «Контрольные работы». Проверочная работа 3 «Углы».
