Задача анализа времени производственного процесса

В качестве первого примера рассмотрим комплекс работ в задаче анализа времени производственного процесса по изготовлению и контролю качества деталей, приведенную в [24, с. 57], и исследуем ее путем построения сетевой модели.

Постановка задачи. На производственыной линии изготавливается деталь. Предполагается, что изготовление занимает четыре часа. Перед началом отделочных работ 25% деталей не проходят проверку, и им может потребоваться доработка. Время проверки предполагается распределенным в соответствии с бета-распределением со средней продолжительностью в один час. Доработка занимает три часа, и 30% переработанных частей не проходят проверку во второй раз. Вторая проверка доработанных деталей также распределяется в соответствии с бета-распределением со средней продолжительностью в полтора часа. При этом время проверок варьируется от 0 до 5 часов.

Детали, не прошедшие проверку, утилизируются. Если деталь проходит одну из инспекций, она отправляется на отделку, которая занимает 10 часов в 60% случаев и 14 часов в 40% случаев. Окончательная проверка, которая занимает один час, исключает 5 процентов деталей, которые затем утилизируются.

Необходимо построить сетевую модель, позволяющую оценить время выполнения комплекса работ. Уже в самой формулировке задачи выясняется необходимость использования вероятностной модели (вероятностное задание времени) и недетерминированность структуры сети (деталь может потребовать доработки, но не в каждом случае), что обусловливает использование альтернативной сети.

Структурное разбиение работ. Главная цель комплекса работ – получение готовых деталей из исходного материала. Итогами работы может стать успешное завершение изготовления или утилизация детали.

Рис. 2.1. СРР для задачи 1.

Основные составляющие производства: изготовление детали, проверка, отделка. На Рис. 2.1. СРР для задачи 1 представлена иерархическая структура работ по производству детали.

Сетевая модель. Для создания сетевой модели построим таблицу процессов (Таблица 2.1), в которой в первом столбце стоит наименование выполняемой работы, во втором – код работы. В столбцах «Вероятность» и «Время» указаны соответствующие этим работам параметры: время выполнения в часах и вероятность выполнения. Записи «β1» и «β2» в графе «Время» обозначают вероятностное время, заданное с помощью бета-распределения со следующими параметрами:

для β1 ,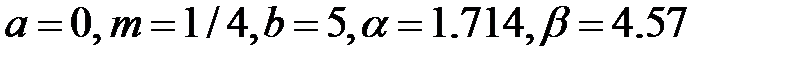

для β2 .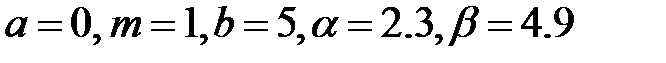

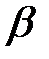Значения , и получены с помощью формул (1.18), (1.16) и (1.17) соответственно.

Таблица 2.1.

Взаимосвязи работ при производстве деталей.
Наименование работы	Код работы	Вероятность	Время выполнения , часов
Изготовление детали	0,1
Первичная проверка (неудачная)	1,2	0,25	β1
Первичная проверка (успешная)	1,5	0,75	β1
Доработка детали	2,3
Проверка доработанной детали (неудачная)	3,4	0,3	β2
Проверка доработанной детали (успешная)	3,5	0,7	β2
Отделка (медленная)	5,61	0,4
Отделка (быстрая)	5,62	0,6
Окончательная проверка (неудачная)	6,4	0,05
Окончательная проверка (успешная)	6,7	0,95

Сетевая модель типа «узел – событие», построенная по исходным данным представлена на рисунке (

Рис. 2.2). В дугах указаны вероятности осуществления работ и время их выполнения. Над дугами указаны соответствующие им названия работ.

Начальное событие обозначено «0», завершение изготовления детали – «7», утилизация – «4». Промежуточные события обозначены цифрами 1, 2, 3, 5, 6. События 1, 3 имеют альтернативы только на выходе, события 5, 6 – альтернативного характера на входе и выходе.

Рис. 2.2. Сетевая модель производства детали.

По построенной сетевой модели сразу же можно определить вероятности исходов «4» и «7» с использованием теорем сложения и умножения вероятностей.

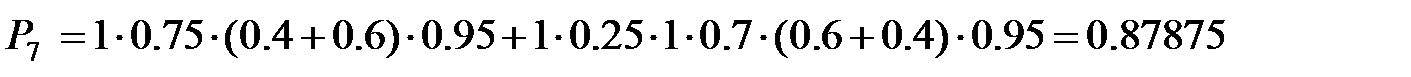,	(2.1)
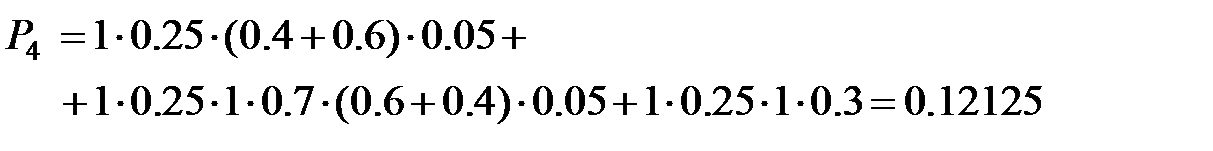	(2.2)

Оптимизация. Теперь оптимизируем сеть с помощью описанных в пункте 1.4.4 преобразований. Во-первых, сократим параллельные дуги (5,6¹ и 5,6²), и элементарные последовательности из двух дуг (

Таблица 2.2).

Таблица 2.2.

Элементарные преобразования в сетевой модели.

Сокращаемые дуги	Изменяемые дуги	Полученные дуги	Вероятности	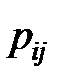Время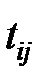
5,6i	5,61	5,6		11,6
5,62
0,1	1,2	0,2	0,25	4+β1
1,5	0,5	0,75	4+β1
2,3	3,4	2,4	0,3	3+β2
3,5	2,5	0,7	3+β2
5,6	6,4	5,4	0,05	12.6
6,7	5,7	0,95	12.6

После этих преобразований сеть содержит только альтернативные вершины и выглядит следующим образом (Рис. 2.3):

Рис. 2.3. Промежуточный этап оптимизации.

Дальнейшие сокращения выполненные в указанной последовательности, приведены в таблицеТаблица 2.3.

Таблица 2.3.

Преобразования сети (минимизация).

Сокращаемые дуги	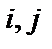Изменяемые дуги	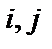Полученные дуги	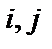Вероятности	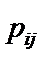Время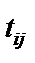
0,2	2,4	0,4	0.075	7+ β1+ β2
2,5	0,52	0.175	7+ β1+ β2
0,5i	0,51	0,5	0.925	4.225+0.925 β1+ 0.175 β2
0,52
0,5	5,4	0,42	0.04625	16.825 + 0.925 β1 + 0.175 β2
5,7	0,7	0.87875	15.086+0.87875 β1+0.16625 β2
0,4i	0,41	0,4	0.12125	1.30316 + 0.11778 β1 + 0.08309 β2
0,42

Эти преобразования приводят к сети, в которой есть только начальный и два конечных узла, и две дуги, соединяющие их (

Рис. 2.4).

Рис. 2.4. Результат минимизации сети.

Выводы. Вероятности выполнения конечных узлов получились равными ранее вычисленным в (2.1) и (2.2), что свидетельствует о правильной минимизации сети. Подставив вместо β1 и β2 соответствующее 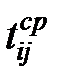и просуммировав, получим усреднённую оценку времени достижения одного из конечных событий.

Таким образом, среднее время изготовления качественной детали составляет ~ 16.21 часа или 16 часов 13 минут, а вероятность этого исхода составляет ~ 87.9%.