Результаты расчётов показателей безотказности

Δt, часов	0-100	100-200	200-300	300-400	400-500	500-600	600-700
Σr(Δt)
r(t)
P(t)	0,984	0,932	0,852	0,789	0,716	0,674	0,642
Q(t)	0,016	0,068	0,148	0,211	0,284	0,326	0,358
a(Δt)∙10-4	1,578	5,263	7,894	6,315	7,368	4,211	3,158
λ(Δt)∙10-4	1,591	5,494	8,849	7,692	9,79	6,061	4,8
ω(Δt)	11,046	36,841	55,258	44,205	51,576	29,477	22,106

Контрольные вопросы:

1. Дайте определение надёжности. Из каких свойств она состоит?

2. Перечислите основные единичные показатели безотказности сложных технических объектов.

3. Назовите единицы измерения данных показателей.

4. Дайте определение вероятности безотказной работы объекта.

5. Что называют вероятность отказа?

6. Что характеризует частота отказов?

7. Дайте определение интенсивности отказов.

8. Какие три этапа можно выделить на графике изменения интенсивности отказов?

9. Что характеризует параметр потока отказов?

10. Дайте определение средней наработке на отказ.

ВЕРОЯТНОСТНАЯ ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЁЖНОСТИ

Задача №2.

Рассчитать численные значения статистических характеристик для нормального закона распределения случайных величин (время работы до отказа). Построить гистограмму распределения времени работы до отказа объекта, полигон фактической и расчётной вероятностей отказа, а также графики изменения интегральной функции вероятности отказа и безотказной работы.

Проверить выдвинутую гипотезу с помощью критерия Пирсона.

Решение.

Время работы объекта до отказа l, мес., представлено в табл.3.1.

Таблица 3.1

1. Случайные величины располагаем в порядке возрастания.

l_min = 5; 11; 18; 25; 29; 31; 36; 41; 45; 48; 48; 50; 56; 59; 62; 65; 66; 69; 70; 72; 72; 74; 75; 79; 81; 84; 85; 88; 89; 91; 98; 107; 112; 114; 118; l_max = 129 месяцев.

2. Определяем размах случайной величины R, мес.:

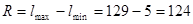(3.1)

3. Определяем количество интервалов, на которое следует разбить статистических ряд случайных величин.

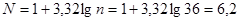(3.2)

где n – число значений в статистической совокупности случайных величин согласно заданию.

Округляем полученное значение до целого в большую сторону, т.е.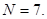

4. Находим ширину интервала А, мес.:

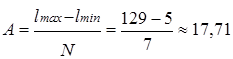. (3.3)

Принимает ширину интервала А равной 20 месяцев, поэтому статистический ряд разбиваем на 7 равных по величине интервалов. Для удобства последующих построений и расчётов длину интервала А следует принимать кратной пяти, т.е. 5, 10, 15 месяцев и т.д.

Результаты заносим в табл.3.2 (2 столбец). В 3 столбец заносим середины интервалов l_серi , мес.

5. Производим группировку, т.е. определяем число случайных величин в первом, втором и последующих интервалах. Количество случайных величин, попавших в определенный интервал называется частотой m_i. Полученные результаты также заносим в табл.3.2 (4 столбец). С учётом имеющихся данных, строим гистограмму распределения времени работы объекта до отказа (рис.3.1, а).

Таблица 3.2

Сводная таблица статистической оценки времени работы

Объекта до отказа

Номер интер-вала Ni	Интер-вал ∆l, мес.	Сере-дина интер-вала lсерi , мес.	Час-тота, mi, шт.	Часто-сть, ωi→рi	Дифферен-циальная функция распреде-ления f(li)	Вероят-ность Рi*	Оценка накопленных вероятностей
отказа Fi	безотказ-ности Ri
1.	0-20			0,0556	0,0008	0,0163	0,0163	0,9837
2.	20-40			0,1111	0,0034	0,0694	0,0857	0,9143
3.	40-60			0,2222	0,0087	0,1776	0,2633	0,7367
4.	60-80			0,2778	0,0134	0,2734	0,5367	0,4633
5.	80-100			0,1944	0,0127	0,2592	0,7959	0,2041
6.	100-120			0,1111	0,0074	0,1510	0,9469	0,0531
7.	120-140			0,0278	0,0026	0,0531	1,0000
Всего	-	-			0,0490	1,0000	-	-

6. Определяем частость ω_i. Частость является эмпирической величиной и служит для оценки вероятности. Как было отмечено ранее, при увеличении числа наблюдений частость приближается к вероятности: ω_i → р_i.

, (3.4)

;

;

...

.

Полученные при группировке времени работы объекта до отказа сводим в табл.3.2 (столбец 5).

7. Определяем среднее значение времени работы до отказа объекта М, мес., т.е.

. (3.5)

8. Определяем среднеквадратическое отклонение σ, мес.:

. (3.6)

9. Определяем коэффициент вариации υ:

.

Находим значения дифференциальной функции распределения. С учётом того, что значение коэффициента вариации υ<0,4, для заданной статистической совокупности предпочтителен нормальный закон распределения, т.е.

, (3.7)

;

;

...

.

Для упрощения расчётов можно принять = 2,718.

Найденные значения заносим в 6 столбец табл.3.2.

10. Определяем вероятность отказа Р_i*, т.е. отношение числа случаев, благоприятствующих возникновению событий, к общему числу случаев:

, (3.8)

...

.

Найденные значения заносим в 7 столбец табл.3.2.

11. Определяем вероятность отказов F_i, которая может быть получена суммированием интервальных вероятностей за наработку l_i:

, (3.9)

;

;

...

.

Полученные значения заносим в 8 столбец табл.3.2.

12. Определяем вероятность безотказности работы R_i:

, (3.10)

;

;

...

.

Полученные значения заносим в 9 столбец табл.3.2.

По данным табл.3.2 строим графики: ; ; ; (рис.3.2 б, в). Для удобства данные графики располагаем непосредственно под гистограммой распределения времени работы объекта до отказа.

13. Проверка выдвинутой гипотезы с помощью критерия согласия Пирсона χ².

Для определения χ² строят укрупнённый статистический ряд, соблюдая условие: N_у>4, m_i≥5.

При этом допускается объединение соседних рядов, в которых m_i<5. В связи с этим первый и второй, а также шестой и седьмой интервалы статистического ряда объединяют (табл.3.3). Опытная частота в объединённом интервале будет равна сумме частот объединяемых интервалов. В остальных интервалах статистического ряда опытные частоты больше пяти, поэтому эти интервалы оставляем без изменения.

Таблица 3.3

Определение интегральной функции F(t_i)и теоретической частоты mt_i

Номер интервала NУ	Укрупнённый интервал ∆lу, мес.	Укрупнённая частота mi, шт.	Интегральная функция F(ti)	Теоретическая частота mti
1.	0-40		0,09	3,24
2.	40-60		0,27	6,48
3.	60-80		0,54	9,72
4.	80-100		0,78	8,64
5.	100-140		0,99	7,56
Всего:	-		-	-

Для определения интегральной функции F(t_i) через F₀(t_i) (Приложение 4) при нормальном законе распределения применяем уравнение:

, (3.11)

;

...

.

Теоретическая частота mt_i равна

, (3.12)

;

...

.

Критерий согласия Пирсона χ² определяется по уравнению

. (3.13)

По сводной таблице (Приложение 5) для α = 0,05 и числу степеней свободы r = N_у-1-2 = 5-1-2=2 (где N_у - число укрупнённых интервалов) находим табличное значение χ²_{0,05; r=2} равное 6,0.

В нашем случае χ²_0,05; r > χ², полученного по формуле 3.13, поэтому гипотеза о принятом нормальном законе распределения случайной величины подтверждается.

Контрольные вопросы:

1. Какие законы распределения случайных величин существуют?

2. Каким образом определяется коэффициент вариации?

3. Что такое частота случайных величин?

4. Каким образом определяется частость случайных величин?

5. Каким образом определяется нормальный закон распределения случайной величины?

6. Чем отличается дифференциальное и интегральное распределение случайной величины?

7. Если на протекание исследуемого процесса и его результат влияет сравнительно большое число случайных и взаимозависимых факторов, интенсивность действия которых зависит от достигнутого случайной величиной состояния, условия для какого закона распределения возникают?

8. Какой закон распределения чаще всего используется при описании внезапных отказов, продолжительности ремонта?

9. Каким образом определяется размах случайной величины?

10. Какой критерий согласия используют при проверке совпадение опытного и теоретического законов распределения случайной величины?

а) Гистограмма распределения времени работы объекта до отказа

Рис.3.1. Графическое изображение времени работы до отказа объекта,

как случайной величины

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Животкевич И.Н., Смирнов А.П. Надёжность технических изделий. М.: Олита, 2003. - 472 с.

2. Кочерга В.Г. Основы теории надёжности оборудования нефтегазовых объектов: учеб. Пособие. - Хабаровск: Изд-во ДВГУПС, 2014. - 95 с., ил.

3. Курчаткин В.В. Надёжность и ремонт машин. - М.: КолосС, 2000. - 776 с.

4. Методика сбора и обработки данных по надёжности автомобилей: учеб. пособие / Сост. В.В. Савельев. - Самара: Самар. гос. техн. ун-т, 2013. - 103 с., табл., илл.

5. Ушаков И.А. Курс теории надёжности систем: уч. пособие для вузов / И.А. Ушаков. - М.: Дрофа, 2008. - 239 с.

6. Шторм Р.А. Теория вероятностей. Математическая статистика. Статистический контроль качества. Изд-во "Мир", Москва, 1970. - 368 с.

7. Шубин В.С., Рюмин Ю.А. Надёжность оборудования химических и нефтеперерабатывающих производств. - М.: Химия, КолосС, 2006. - 359 с.: ил. - (Учебники и учеб. пособия для студентов высш. учеб. заведений).

Приложение 1