Метод прогноза и коррекции для решения задачи Коши

Отличительной чертой методов Рунге-Кутта является то, что при вычислении следующей точки (x[m+1], y[m+1]) используется информация только об одной предыдущей точке (x[m], y[m]), но не нескольких. Кроме того, для методов Рунге-Кутта отсутствуют достаточно простые способы оценки ошибки, что приводит к необходимости рассмотрения некоторых дополнительных методов решения ДУ.
Отличительное свойство этих методов состоит в том, что с их помощью нельзя начать решение уравнения т.к. в них необходимо использовать информацию о предыдущих точках решения. Чтобы начать решение, имея только одну точку, определяемую начальными условиями, или для того, чтобы изменить шаг (h), необходим метод типа Рунге-Кутта. Поэтому приходится использовать разумное сочетание этих двух методов.
Методы, которые мы рассмотрим, известны под общим названием методов прогноза и корректировки. Как ясно из названия вначале «предсказывается» значение y[m+1], а затем используется тот или иной метод его «корректировки».

Метод Адамса-Бошфора

Экзаменационный билет № 16

Многочлены Чебышева и их свойства

См. книгу Турчака, стр. 39

Свойства:

• Многочлены четных степеней — четные функции, а нечетных — нечетные.

• Сумма коэффициентов первого рода равняется 1, а второго k+1.

Определитель и обратная матрицы, их вычисление

См. билет 14.

Численные методы решения задачи Коши для систем дифференциальных уравнений первого порядка

Экзаменационный билет № 17

Рациональное приближение. Аппроксимация обобщенными многочленами

Рациональное приближение: см. стр 44 (Турчак)

Приближение, полученное с помощью отношения двух алгебраических многочленов 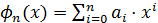и .

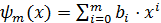Метод прогонки

г) метод прогонки. Данный метод применяется для решения трех диагональных систем:

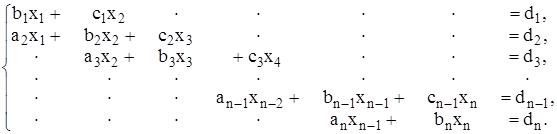
(2.9)

Метод состоит из двух этапов прямой прогонки - и обратной прогонки.

Прямая прогонка: Величина x_i выразим через x_i+1 с помощью коэффициентов A_i, B_i

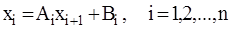. (2.10)

Из первого уравнения находим значения A₁ и B₁:

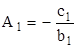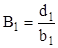, . (2.11)

Подставляя x₁=A₁·x₂+B₁ во второе уравнение (2.9) имеем:

a₂(A₁x₂+B₁)+b₂x₂+c₂x₃=d₂,

или

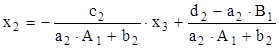
Отсюда согласно (2.10) находим A₂ и B₂

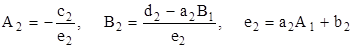, (2.12)

т.е. зная A₁ и B₁ по этой формуле мы можем вычислить A₂ и B₂. Аналогично подставляя значение x_i-1=A_i-1x_i+B_i-1 в i уравнение имеем:

a_i(A_i-1x_i+B_i-1)+b_ix_i+c_ix_i+1=d_i, i=1,2,...n.

Если в формуле (2.12) индекс 1 заменить на индекс i-1, а индекс 2 - на индекс i, то получим общую формулу для прямой прогонки:

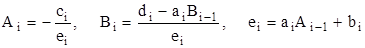, i=2,...,n; (2.13)

которая позволяет определить последующие значения A_i, B_i через предыдущие A_i-1, B_i-1.

После n шагов получим значения A_n и B_n. Так как c_n=0, то A_n=0. Следовательно на основание (2.10) имеем: x_n=B_n.

Обратная прогонка состоит в последовательных вычислениях по формуле (2.10) значений x_n-1, x_n-2 и т.д. до x₁.

Если для трех диагональной системы выполнены условия çb_iç³ça_iç+çc_iç, ½b_i½>½a_i½, i=1,...,n, то эта система имеет единственное решение.