Задача Коши для дифференциального уравнения первого порядка. Теорема существования решения задачи Коши. Интегральные кривые

Обыкновенным дифференциальным уравнением называется уравнение, которое содержит производные от искомой функции y(x):

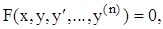(2.1)

где x - независимая переменная, (n) - порядок производной. Наивысший порядок n, входящий в уравнение (2.1) называется порядком дифференциального уравнения.

Общее решение дифференциального уравнения имеет вид:

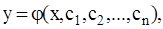(2.2)

где c₁,c₂,...,c_n - произвольные постоянные. Их количество определяется порядком уравнения.

Если значения c₁,c₂,...,c_n известны и соответственно равны 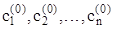, то из (2.2) получаем частное решение:

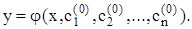
Значения 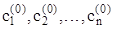определяются из условий, которые называются дополнительными условиями для уравнения (2.1).

Графики частных решений называются интегральными кривыми для данного дифференциального уравнения. Общее решение можно представить в виде семейства интегральных кривых.

Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задачи Коши называются начальными условиями, а точка x=x₀, в которой они задаются - начальной точкой.

Если дополнительные условия задаются в двух точках a и b - “краях” отрезка [a,b], где ищется решение, то такая задача называется краевой задачей.

Дифференциальное уравнение первого порядка:

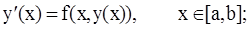(2.4)

при заданных начальных условиях y(x₀)=y₀ называется задачей Коши для дифференциального уравнения первого порядка.

Если мы имеем систему дифференциальных уравнений первого порядка, то задачу Коши удобно записать в векторной форме:

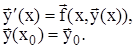
Теорема существования решения задачи Коши

Интегральные кривые

Экзаменационный билет № 10

Корректность вычислительных алгоритмов. Три условия корректности вычислительного алгоритма. Обусловленность вычислительного алгоритма

Корректность вычислительных алгоритмов

1. Результат получен после конечного числа шагов

2. Результат устойчив к малым возмущения входных данных

3. Результат обладает вычислительной устойчивостью.

4.

Метод Монте-Карло для задач вычисления кратных интегралов

Формула (5.33) непосредственно обобщается на кратные интегралы

,

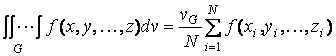где 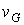– объем области интегрирования. Например, для двукратного интеграла с прямоугольной областью интегрирования имеем

.

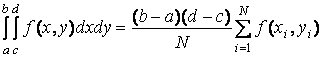Модификации метода Эйлера второго порядка точности для дифференциального уравнения первого порядка

Метод трапеции. В этом методе решение имеет вид:

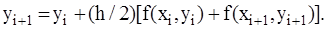(2.9)

Этот метод неявный, т.к. для определения значений y_i+1 необходимо решать нелинейное уравнение (2.9). Метод трапеций имеет второй порядок точности по h.

метод Эйлера-Коши. Данный метод является прямым методом второго порядка точности:

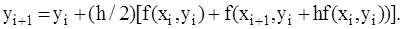(2.10)

Экзаменационный билет № 11

Требования, предъявляемые к вычислительным алгоритмам. Требования к программным реализациям вычислительной задачи

Требования к вычислительным алгоритмам

1. Экономичность(число элементарных операций)

2. Надлежащая точность(решение задачи с заданной или приемлемой точностью)

3. Экономия памяти(-)

4. Простота

Требования к программным реализациям алгоритмов

1. Надежность(без ошибок)

2. Работоспособность

3. Переносимость

4. Поддерживаемость

5. Простота