Волновая поверхность. Фронт волны.

Волны

Волна – процесс распространения колебаний в пространстве.

По природе:

-физические (механические, электромагнитные)

-химические

-биологические

Общим свойством всех волн любой природы является перенос Е без переноса вещества.

Линия, вдоль которой происходит перенос Е, называется лучем.

Частным случаем механических волн, являются упругие волны – это распространение деформации в упругих средах.

Упругая среда – это среда м/у частицами, м/у которыми существуют силы взаимодействия вызывающие упругую деформацию этой среды (твердые тела, жидкости, газы).

В вакууме, где достаточно сильно разряженные частицы и силы взаимодействия незначительны, механические волны не распространяются.

Колебания, возбужденные в какой-либо точке среды распространяются в ней со скоростью, зависящей от свойств среды (в частности от плотности среды), передавая возбуждение от одной точке среды к другой – max в твердых телах, min в газах.

По направлению смещения частиц среды различают волны:

-продольные

-поперечные

Продольные – волны, в которых колебания частиц происходят вдоль луча. Они м/т распространятся в средах, в результате возникновения упругих сил при деформации сжатия и растяжения (твердые, жидкие и газообразные тела).

Луч

колебания частиц

Поперечные – волны, колебания частиц которых происходят перпендикулярно лучу.

Они распространяются в средах, в которых возникают упругие силы при деформации сдвига (твердые тела)

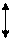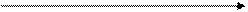Луч

При растяжении – длина волны увеличивается, при сжатии – уменьшается.

Таким образом, продольные волны во всех телах, поперечные только в твердых.

Волновая поверхность. Фронт волны.

Волновая поверхность – геометрическое место точек колеблющихся в одной фазе.

Фронт волны – пограничная волновая поверхность отделяющей среду возмущенную от среды невозмущенной.

По форме волновые поверхности:

-плоские

-сферические

-цилиндрические

Волновые поверхности плоских волн – совокупность параллельных плоскостей, перпендикулярных направлению распространения волны.

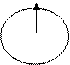
Для сферических волн, волновая поверхность - это концентрическая сфера.

Волновых поверхностей бесчисленное множество.

Фронт волны один и он всегда движется.

Уравнение волн

Уравнение волны в общем виде:

S=f(x,y,z,t), где S – смещение колеблющейся точки, относительно положения равновесия; x,y,z – координаты точки; t – время.

Уравнение сферической волны в общем виде:

S=f(r,t), где r – расстояние от источника до данной точки (радиус сферы).

Уравнение плоской волны в общем виде:

S=f(x,t)

Дифракция волн

Дифракция – отклонение волны от прямолинейного распространения в среде с неоднородностями (препятствие, отверстие).

Дифракция – огибание волной препятствий размеры которого (d) соизмеримы с длиной волны λ.

Принцип Гюгенса:

Каждая точка среды, которой достигла волна в данный момент времени t (т.е. каждая точка фронта волны), становится источником вторичных, сферических волн, огибающая которых показывает положение фронта волны в следующий момент времени t+∆t.

S=υ∆t

Принцип Гюгенса позволяет определить фронт волны в следующий момент времени и качественно оценить дифракцию механических волн.

Пусть плоская волна попадает на поверхность экрана в котором имеется отверстие:

d>>λ   Только на боковых границах волнового фронта наблюдается отклонение от прямолинейного распространения.

d<=λ     Вторичные волны образуют за экраном расходящиеся сферические волны.

Интерференция волны

Интерференция – явление наложения когерентных волн, вследствие которого наблюдается устойчивое во времени усиление или ослабление амплитуды результирующих колебаний в различных точках пространства.

Интерференция – общее свойство волн любой природы.

Устойчивая картина интерференции м/т наблюдаться только при сложении когерентных волн.

Когерентными называют волны (и их источники) имеющие постоянные разность фаз и одинаковую частоту.

Условие когерентности:

φ₀=const

ν₁=ν₂

Пусть в т. О₁ и О₂ находятся когерентные источники волн (предположим что волны встречаются).

r₁

О₁

∆r

r₂

О₂

r-геометрическая длина пути – расстояние, которое волна проходит от источника до места встречи.

[r]=м

∆r – геометрическая разность хода

∆r=r₁-r₂

В нашем случае: ∆r=r₂-r₁

[∆r]=м

1 способ – перпендикуляр

2 способ - с помощью циркуля

Напишем уравнение волн, распространяющихся от источников О₁ и О₂:

S₁=AsinW(t-r₁/υ)

S₂=AsinW(t-r₂/υ)

Α=W(t-r₁/υ)

S_рез=S₁+S₂

sinα+sinβ=2sin(α-β)/2*sin(α+β)/2

S_рез=2Acos(Wt-Wr₁/υ-Wt+Wr₂/υ)/2 * sin(Wt-Wr₁/υ+Wt-Wr₂/υ)/2

S_рез=2Acos*W/2υ*∆r * sin*Wt-W/2υ(r₁-r₂)

S_рез=A_резsin(Wt+φ_0рез)

Складываются 2 волны

В результате сложения когерентных волн получают гармоническое колебание, которое происходит с той или иной частотой W. A_рез и φ_0рез зависят от величины геометрической разности хода ∆r.

Условия максимума

A_рез=2Acos*W∆r/2υ

W∆r/2υ=Ф

A_рез max если cosФ=1

W∆r/2υ=kπ

W=2π/T

υ=λ/T

2π∆rT/T2λ=kπ à ∆r=kπ – условие максимума

Геометрическая разность хода равна целому числу.

∆r=2kπ/2 – условие максимума интерференции (k-порядок максимума = 0,1,2,3…)

Геометрическая разность хода ∆r укладывается четное число длин полуволн λ/2. Волны от источника в данную точку приходят в фазе.

A_рез=A₁+A₂=A_max

Если амплитуда равны (A₁=A₂), то А_рез=2A

В этих точках происходит взаимное усиление волн. Эти точки называют максимумами интерференции.

Условия минимума

A_рез min если cosФ=0

W∆r/2υ=(2k-1)*π/2

2π∆rT/T2λ=(2k-1)π/2 à ∆r=(2k+1)π/2 – условие минимума (k-порядок минимума = 0,1,2,3…)

Геометрическая разность хода ∆r укладывается нечетное число длин полуволн λ/2. Волны от источника в данную точку приходят в противофазе (∆φ=π; 3π; 5π)

A_рез=⃒A₁-A₂⃒=A_min

Если амплитуда равны (A₁=A₂), то А_рез=0

В этих точках происходит взаимное ослабление волн. Эти точки называют минимумами интерференции.

В остальных точках пространства: Amin < A_рез < A_max

Интерференционная картина – устойчивая во времени и пространстве картина чередования максимумов и минимумов.

Длина бегущей волны.

λ_бег.=λ_ст

Распределенными называется системы, в которых параметры системы распределены в пространстве.

Распределенными системами являются ящики, закрытые с одной или с двух сторон – резонаторы.

В частности такие системы как ротовая полость, слуховой проход являются примерами распределенных систем.

L =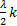

Волны

Волна – процесс распространения колебаний в пространстве.

По природе:

-физические (механические, электромагнитные)

-химические

-биологические

Общим свойством всех волн любой природы является перенос Е без переноса вещества.

Линия, вдоль которой происходит перенос Е, называется лучем.

Частным случаем механических волн, являются упругие волны – это распространение деформации в упругих средах.

Упругая среда – это среда м/у частицами, м/у которыми существуют силы взаимодействия вызывающие упругую деформацию этой среды (твердые тела, жидкости, газы).

В вакууме, где достаточно сильно разряженные частицы и силы взаимодействия незначительны, механические волны не распространяются.

Колебания, возбужденные в какой-либо точке среды распространяются в ней со скоростью, зависящей от свойств среды (в частности от плотности среды), передавая возбуждение от одной точке среды к другой – max в твердых телах, min в газах.

По направлению смещения частиц среды различают волны:

-продольные

-поперечные

Продольные – волны, в которых колебания частиц происходят вдоль луча. Они м/т распространятся в средах, в результате возникновения упругих сил при деформации сжатия и растяжения (твердые, жидкие и газообразные тела).

Луч

колебания частиц

Поперечные – волны, колебания частиц которых происходят перпендикулярно лучу.

Они распространяются в средах, в которых возникают упругие силы при деформации сдвига (твердые тела)

Луч

При растяжении – длина волны увеличивается, при сжатии – уменьшается.

Таким образом, продольные волны во всех телах, поперечные только в твердых.

Волновая поверхность. Фронт волны.

Волновая поверхность – геометрическое место точек колеблющихся в одной фазе.

Фронт волны – пограничная волновая поверхность отделяющей среду возмущенную от среды невозмущенной.

По форме волновые поверхности:

-плоские

-сферические

-цилиндрические

Волновые поверхности плоских волн – совокупность параллельных плоскостей, перпендикулярных направлению распространения волны.

Для сферических волн, волновая поверхность - это концентрическая сфера.

Волновых поверхностей бесчисленное множество.

Фронт волны один и он всегда движется.

Уравнение волн

Уравнение волны в общем виде:

S=f(x,y,z,t), где S – смещение колеблющейся точки, относительно положения равновесия; x,y,z – координаты точки; t – время.

Уравнение сферической волны в общем виде:

S=f(r,t), где r – расстояние от источника до данной точки (радиус сферы).

Уравнение плоской волны в общем виде:

S=f(x,t)