Продолжительность этапов работ проекта

№ п/п	Этап работ	Продолжительность	№ п/п	Этап работ	Продолжительность
	A	5 дней	6.	F	15 дней
1.	B	7 дней	7.	G	8 дней
2.	C	10 дней	8.	H	10 дней
3.	D	15 дней	9.	I	7 дней
4.	E	10 дней	10.	J	7 дней
	Итого: 86 дней

Задание: построить сетевой график выполнения работ, определить критический путь.

Решение. На первом шаге определяем позиционный вес каждого этапа работ. Позиционный вес этапа работ — это продолжительность самого этапа плюс сумма продолжительности цепочки всех последующих этапов работ

Таблица 1

№ п/п	Этап работ	Позиционный вес
1.	A	5+10+15+7+7=44
2.	B	7+15+7+7=36
3.	C	10+8+10+7+7=42
4.	D	15+10+7+7=39
5.	E	10+15+7+7=39
5.	F	15+7+7=29
6.	G	8+10+7+7=32
7.	H	10+7+7=24
8.	I	7+7=14
9.	J

На втором шаге упорядочиваем этапы работ в порядке убывания позиционных весов и отмечаем предшествующие этапы работ (табл. 2).

Таблица 2

Упорядоченные этапы работ

№ п/п	Этап работ	Позиционный вес	Предшествующие этапы работ
1.	A		-
2.	B		-
3.	C		-
4.	D		A
5.	E		-
10.	F		C
11.	G		E, B, G
12.	H		G, D
13.	I		F, H
14.	J		I

Следующий шаг - непосредственное построение сетевого графика.

При построении сетевых графиков используют ряд обозначений:

· этапы работ изображаются стрелками;

· каждая стрелка имеет начало и конец, называемые событиями, которые изображаются кружком («узел»);

· последовательность этапов работ называется «путем»; длина стрелок не имеет значения; время измеряется слева направо;

· этап работ не может быть выполнен, пока не будут завершены все предыдущие этапы (слева от узла);

· этапы с нулевой продолжительностью называют фиктивными этапами. Их включают в схемы для ликвидации неувязок и последовательности выполнения этапов, обозначая стрелками с пунктирной пинией.

На рис. 17 изображен сетевой график для нашей задачи. Он построен путем обратного следования от конечного события к начальному по табл. 2. На графике изображены фиктивные этапы работ, введенные с целью выполнения условия, что этап G не может быть начат раньше окончания этапа F.

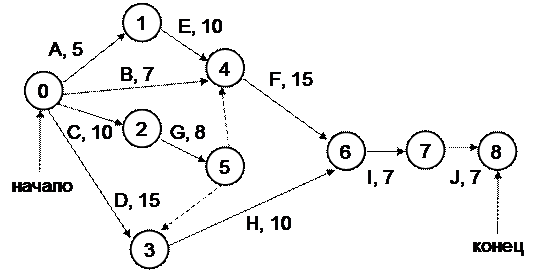
Рис. 17 Сетевой график

Из сетевого графика видно существование нескольких путей с различной степенью важности. Путь с самым продолжительным временем реализации определяет минимальный срок выполнения всего проекта в целом и называется критическим путем.

На рис. 8 выделен критический путь для построенного сетевого графика. Продолжительность критического пути составляет 47 дней. Следует отметить, что при последовательном выполнении этапов работ потребовалось бы 86 дней, т.е. последовательно-параллельное ведение этапов работ позволяет сократить срок выполнения проекта на 39 дней.

Важной информацией для исполнителей проекта служат значения наиболее ранних и поздних сроков наступления событий. Знание этих параметров позволяет рационально варьировать имеющимися в распоряжении ресурсами.

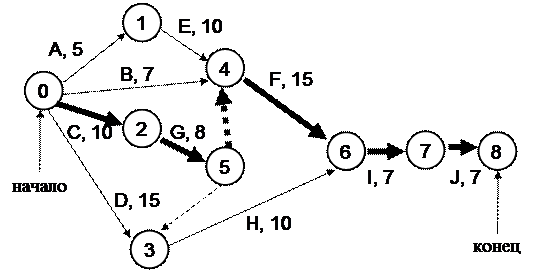
Рис. 18. Критический путь

Наиболее ранние сроки рассчитываются от начала графика (слева направо) и равны сумме продолжительности предшествующих операций. Наиболее поздние сроки рассчитываются с конца графика. Для определения наиболее позднего срока наступления события из продолжительности критического пути нужно вычесть сумму продолжительности самого и последующих, этапов. Для событий, принадлежащих критическому пути, наиболее ранние и поздние сроки наступления совпадают.

Определим ранние и поздние сроки наступления событий 4, 3 и 1.

Событие 4 принадлежит критическому пути, поэтому наиболее ранний и поздний сроки наступления события совпадают иравны 18 дням (продолжительность этапа С плюс продолжительность этапа G).

Наиболее ранний срок наступления события 1 равен 5 дням (продолжительности этапа А). Наиболее поздний срок наступления события 1 равен 8 дням (наиболее поздний срок наступления события 4 минус продолжительность операции Е).

Наиболее ранний срок наступления события 3 равен 15 дням (продолжительности этапа D). Наиболее поздний срок наступления события 3 равен 18 дням (наиболее поздний срок наступления события 4 минус продолжительность двух фиктивных операций, которая, естественно, равна нулю).

Литература

Аникин Б.А. Высший менеджмент для руководителей: Учеб. пособие. - М.: ИНФРА-М, 2000.

Ахъюджа X. Сетевые методы управления в проектировании и производстве. - М.; Мир, 1979.

Бигелъ Дж. Управление производством.- М.: Мир, 1973.

Вагнер Г. Основы исследования операций. В 3 томах. - М.: Мир, 1973.

Гаджичский A. M. Логистика: учебник. - М.: Маркетинг, 2003.

Захаров М. Н. Контроллинг на предприятии (на примере германского акционерного общества "Рургаз"). Методические указания. - М.: Нефть и газ, 1996.

Зубарева В.Д., Саркисов А.С., Андреев А.Ф. Проектные риски в нефтегазовой промышленности: учеб. пособие. - М.: Нефть и газ , 2005.

Колобов А.А., Омельченко И.Н. Основы промышленной логистики. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1998.

Кузнецов А.И., Омельченко И.Н. Технология бизнес - планирования: учеб. пособие / Под ред. А.А, Колобова. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2005.

Липсиц И.В., Коссов В.В. Инвестиционный проект: методы подготовки и анализа. - М.: Бек, 1996.

Логистика: учебник / Под ред. Б.А. Аникина. - М.: ИНФРА-М, 2000.

Приложение 4

Министерство образования и науки РФ

Государственное бюджетное образовательное учреждение

высшего профессионального образования

«Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации»

Тульский филиал

Кафедра менеджмента

Пример выполнения

Курсовая работа

по методам принятия управленческих решений

вариант № 2

Выполнил: студент(ка) __ курса

специальности _____

_________группы

____Ф.И.О___________

Проверил: проф. Арсеньев Ю.Н.

Тула 2014

Общее задание. Вы топ-менеджер одного из субъектов хозяйствования Тульской области. Перед вами поставлены разные 2 из 4 описанных заданий, связанных с принятием решений по моделированию и оценке ситуаций, разработкой стратегии развития вашего субъекта хозяйствования.

Варианты заданий приведены в конце описания образцов принятия решений или по желанию студентов выдаются преподавателем.

Задание 1.

Вами получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (X, млн. руб.).

Для принятия управленческого решения Вами требуется:

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

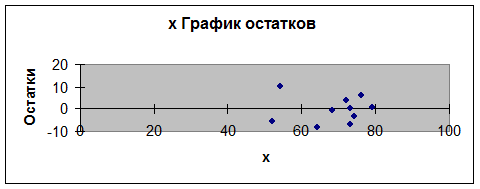
2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков S²ε; построить график остатков.

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α = 0,05).

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F–критерия Фишера (α = 0,05), найти среднюю относительную ошибку аппроксимации. Сделайте вывод о качестве модели.

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α = 0,1, если прогнозное значение фактора Х составит 80% от его максимального значения.

7. Представить графически: фактические и модельные значения Y, точки прогноза.

8. Составить уравнения нелинейной регрессии:

● гиперболической;

● степенной;

● показательной.

Привести графики построенных уравнений регрессии.

9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации.

Сравнить модели по этим характеристикам и выбрать наилучшую модель для развития предприятия.

Таблица 1.1. Исходные данные задачи

Х
Y

Решение.

1.Линейная модель имеет следующий вид:

у = а + вх + ε.

Для расчета параметров а и в решаем систему нормальных уравнений:

nа + в∑х = ∑у

а∑х + в∑х² = ∑ух

Рассчитаем составные элементы данной системы.

По данным табл. 1.2 находим значения неизвестных параметров.

__ _ _

в = 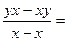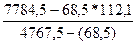= = 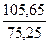1,404

_ _

а = у – вх = 112,1 – 1,4*68,5 = 15,926

Таблица 1.2. Расчетные параметры для линейной модели

_ _ _ _

t	y	x	Yx	x2	y2	(yi - у)	(yi - у)2	(xi - х)	(xi - х)2	ŷ	ε= (yi -ŷ)	|Аi %|
						8,9	79,21	3,5	12,25	117,014	3,986	3,295
						-28,1	789,61	-16,5	272,25	88,934	-4,934	5,874
						6,9	47,61	4,5	20,25	118,418	0,582	0,489
						4,9	24,01	5,5	30,25	119,822	-2,822	2,412
						16,9	285,61	7,5	56,25	122,63	6,37	4,938
						15,9	252,81	10,5	110,25	126,842	1,158	0,905
						-10,1	102,01	-14,5	210,25	91,742	10,258	10,06
						-1,1	1,21	-0,5	0,25	111,398	-0,398	0,359
						-0,1	0,01	4,5	20,25	118,418	-6,418	5,73
						-14,1	198,81	-4,5	20,25	105,782	-7,782	7,941
Сумма							1780,9		752,5
Ср.знач.	112,1	68,5	7784,5	4767,5	12744,5							4,2

Отсюда получается, что ŷ = а + вх, ŷ = 15,926 + 1,404*х = 117,014.

Из линейной модели имеем, что с увеличением объемов капиталовложений на 1 млн. руб. объем выпускаемой продукции увеличится в среднем на 1404 тыс.руб. (1,404).

Коэффициент корреляции: r = 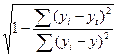= = 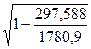0,913,

т.е. связь между объемом капиталовложений и выпускаемой продукции можно считать прямой и тесной, так как | r | > 0,7

Коэффициент детерминации R² = r² = 0,913² = 0,834,

т.е. вариация У (объем выпуска продукции) на 83,4% объясняется вариацией фактора Х (объем капиталовложений).

F – критерий Фишера: F = 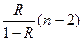= = 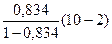40,193. По таблице для a = 0,05; k₁ = m = 1, k₂ = n–m–1 = 8 находим, что F_табл. = 5,32. Т.к. 40,193>5,32, то уравнение регрессии в целом статистически значимо.

Критерий Стьюдента: t_расч = 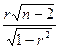= = 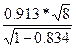= 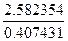6,338.

Табличное значение критерия Стьюдента равно:

t_табл = (a = 0,05; k = n-2=8)=2,3060.

Сравнивая числовые значения критериев, видно, что t_расч > t_табл,, т.е. 6,338 > 2,3060. Таким образом, полученное значение коэффициента корреляции значимо.

Средняя относительная ошибка: Е_отн = 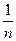∑| |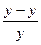* 100% = 4,2%.

Т.е. в среднем расчетные значения ŷ для линейной модели отличаются от фактических значений на 4,2%.

Проверим выполнение предпосылок МНК на основе анализа остаточной компоненты с помощью критерия Дарбина – Уотсона:

(εi--εi-1)2	εi2
79,5664	15,8882
30,42626	24,34436
11,58722	0,338724
84,49286	7,963684
27,16494	40,5769
82,81	1,340964
113,5503	105,2266
36,2404	0,158404
1,860496	41,19072
	60,55952
467,6989	297,588
dw=	1,571632

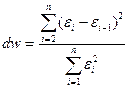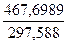= = 1,572.

Сравнение расчетного значения с табличным (d_u=1,32; d_l=0,88) говорит, что ряд остатков не коррелирован, т.к. d_u < dw < 2 (остатки ведут себя как независимые одинаково распределенные случайные величины).

Построим прогноз среднего значения показателя У при уровне значимости α = 0,1, если прогнозное значение фактора Х составит 80% от его максимального значения.

Согласно исходным данным имеем:

х_прогн = 0,8*79 = 63,2

ŷ _прогн = 15,926 + 1,404*0,8*79 = 104,66 млн. руб.

Найдем верхнюю (ŷ _прогн + ∆) и нижнюю (ŷ _прогн - ∆) границу прогноза,

где

∆ = S _ŷ * t_а* 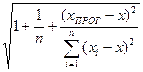, S_ŷ = .

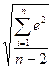Получаем: S_ŷ = 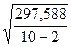= 6,099; t (α = 0,1; k = 8) = 1,8595 и ∑(х_i – х)² = 752,5,

тогда ∆ = 6,099 * 1,8595* 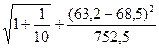= 12,1.

Нижняя граница: 104,66-12,10 = 92,56. Верхняя граница: 104,66+12,10 = 116,76.

Построим ниже полученные уравнения регрессии.

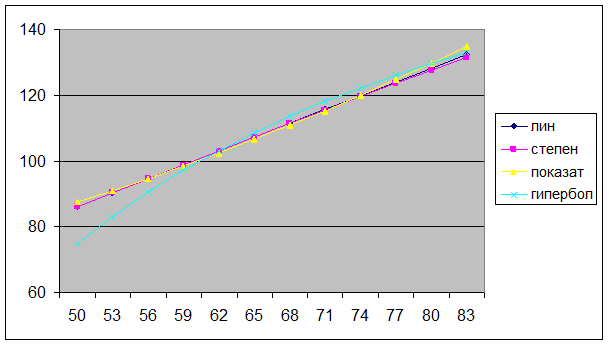
Рис. 1.1. График построенных уравнений регрессии.

Построим степенную модель.

Степенная модель парной регрессии имеет вид:

ŷ = ах^b.

Проведем логарифмирование данной модели:

lg у = lg а + b* lg х

Обозначим через У = lg у, Х = lg х, С = lg а. Тогда имеем:

У = С + b*Х

Значение параметров b и С определим используя данные таблицы 1. 2.

Таблица 1.2. Расчетные параметры степенной модели регрессии

	y	x	У	Х	УХ	Х2	(у-уср.)	(у-уср.)2	ŷ	ε= (yi -ŷ)	ε2	|Аi %|
			2,0828	1,8573	3,8684	3,4497	8,9	79,21	116,8	4,15343	17,2510	3,433
			1,9243	1,716	3,3021	2,9447	-28,1	789,61	88,97	-4,9719	24,7197	5,919
			2,0755	1,8633	3,8674	3,472	6,9	47,61	118,2	0,7958	0,6333	0,669
			2,0682	1,8692	3,8659	3,494	4,9	24,01	119,6	-2,5588	6,5475	2,187
			2,1106	1,8808	3,9696	3,5375	16,9	285,61	122,3	6,74085	45,4390	5,225
			2,1072	1,8976	3,9987	3,601	15,9	252,81	126,3	1,71182	2,9303	1,337
			2,0086	1,7324	3,4797	3,0012	-10,1	102,01	91,83	10,171	103,4496	9,972
			2,0453	1,8325	3,7481	3,3581	-1,1	1,21	111,4	-0,3849	0,1481	0,347
			2,0492	1,8633	3,8184	3,472	-0,1	0,01	118,2	-6,2042	38,4921	5,539
			1,9912	1,8062	3,5965	3,2623	-14,1	198,81	105,9	-7,8707	61,9477	8,031
Сумма			20,463	18,319	37,515	33,592		1780,9		1,58248	301,5583	42,66
Ср.знач.	112,1	68,5	2,0463	1,8319	3,7515	3,3593						4,266

Рассчитаем значения коэффициентов b и С.

b = 0,8375.

С = У – b*Х = 2,0463 – 0,83751*1,8319 = 0,5121.

ŷ = 10^0,5121 * х^0,8375 = ŷ = 3,251622* х^0,8375.

Коэффициент (индекс) корреляции: r = 0,911,

Т.е. связь между объемом капиталовложений и выпускаемой продукции можно считать тесной.

Коэффициент детерминации R² = r² = 0,911² = 0,830, т.е. вариация У (объем выпуска продукции) на 83% объясняется вариацией фактора Х (объем капиталовложений).

F – критерий Фишера: F = 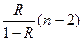= = 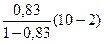39,059. По таблице для a = 0,05; k₁ = m = 1, k₂ = n–m–1 = 8 находим, что F_табл. = 5,32. Т.к. 39,059>5,32, то уравнение регрессии в целом статистически значимо.

Критерий Стьюдента: t_расч = =5,694.

Табличное значение критерия Стьюдента равно: t_табл = (a = 0,05; k = n-2=8)=2,3060,

Сравнивая числовые значения критериев, видно, что t_расч > t_табл, ,т.е. полученное значение коэффициента корреляции значимо.

Средняя относительная ошибка: Е_отн = 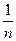∑| |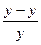* 100% = 4,27%. Т.е. в среднем расчетные значения ŷ для степенной модели отличаются от фактических значений на 4,27%.