Совмещение полигона эмпирического распределения с кривой нормального распределения.
Нормальное распределение является частным случаем биноминального распределения, в котором p=q и n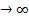 
. Графически оно изображается в виде симметричной (p=q ) и плавно изменяющейся кривой (при n 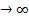полигон превращается в кривую), колоколообразная форма которой выявляется при анализе биномиальных коэффициентов в треугольнике Паскаля уже для n=6, а еще отчетливее – для n=8. Нормальное распределение отражает характер варьирования мерных( непрерывно меняющихся) признаков.
Нормальному распределению подчиняется большая часть биологических признаков. Это обусловлено тем, что в формировании значении биологического признака принимает участие великое множество независимых, случайным образом варьирующих факторов, одни из которых увеличивают это значение, другие с ровной вероятностью уменьшают.
Подавляющее число операций статистической обработки ориентировано на нормальное( или близкое к нему) распределение. Поэтому необходимо знать, подчиняется ли варьирование исследуемого признака закону нормального распределения. Прежде сем сделать заключение о соответствии эмпирического распределения нормальному, нужно предварительно сопоставить частоты ранее полученного вариационного ряда с теоретическими. Высокая наглядность сопоставления достигается на совмещенных графиках кривой нормального распределения и эмпирического полигона, построенных в едином масштабе.
Перед совмещением полигона с кривой нормального распределения необходимо установить, нет ли в исходной выборке сомнительных («выскакивающих») вариант, то есть таких, которые попали в работу случайно и нарушают ее однородность. Эти варианты чрезмерно отклоняются от значения средней арифметической и их сравнительно просто обнаружить и исключить из выборки. В первом приближении можно считать, что к числу «выскакивающих» вариант относятся те, значения которых находятся за пределами границ от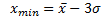 
до 
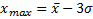(правило «плюс-минус трех сигм).
Существуют и другие способы исключения «выскакивающих» вариант, учитывающие объем выборочной совокупности.
Для рассматриваемого распределения роста девушек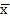 
= 166,1см,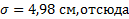 
Xmin = 166,1 – 3 * 4,98 = 151,2см, Xmax = 166,1 + 3 * 4,98 = 181,0 см.
Все 38 значений вариант находятся внутри интервала 151,2 – 181,0 см, то есть «выскакивающих» варианты отсутствуют. Выборки, в которых отсутствуют «выскакивающие» варианты, отвечают требованию типичности.
Чтобы совместить полигон вариационного ряда
Х: 157 161 165 169 173 177
P: 3 8 9 10 7 1
С кривой нормального распределения, необходимо значения классовых вариант представить в нормированной форме, а частоты классов привести к численности нормального распределения. Последнее достигается путем умножения частоты р на модуль
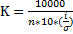, где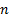 
- объем эмпирической выборки; i – классовый интервал, 
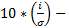операция приведения интервала i в соответствие с интервалом кривой нормального распределения.
Вариационный ряд, по которому строится полигон на графике кривой нормального распределения, имеет следующий вид:
T : -1,82 -1,02 -0,22 0,58 1,38 2,18
P’=pK : 98 262 295 328 229 33
Для сопряженных значений t и p’ с учетом масштаба по оси ординат отложить точки и соединить их отрезками прямой. Это будет полигон эмпирического распределения.