Нормальное распределение и свойства кривой нормального распределения.

Нормальное распределение является частным (предельным случаем биномиального распределения, в котором p=q и n 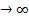. Графически оно изображается в виде симметричной и плавно изменяющейся кривой. Нормальному распеределению подчиняется большая часть биологических признаков. Это обусловлено тем, что в формировании значения биологическорго признака принимает участие великое множество независимых, случайным образом варьирующихся факторов, одни из которых увеличивают, а другие уменьшают это значение. Варьирование происходит относительно среднего значения (предпочтительных признаков для организма), отклонение их в ту или иную сторону по причине мутаций, может привести к гибели организма.

Вероятность нахождения значения биологического признака, подчиняющегося закону нормального распределения, в диапазоне от х до +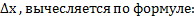

P(х)=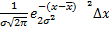

43.

Если зависимость между сопряженными значениями признаков сильно отличается от прямолинейной, используют показатель, кот называется корреляционным отношением (η, греч. «эта»). Оно пригодно для измерения прочности любой связи и выражается в виде двух коэффициентов, которые вычисляются по формулам: η х/у=√1-∑р(х-х⁰ср)^2/∑Рх(х-хср) ^2

η у/х=√1-∑р(у-у⁰ср)^2/∑Ру(у-уср) ^2

Где х,у-срединные значения классов

х⁰ср., у⁰ср,Рх,Ру- берутся из корреляционной решетки

хср,уср- средние арифметические выборочных совокупностей по признакам Х и У.

коэффициенты η х/у и η у/х можно вычислять по другим формулам: : η х/у=√∑Ру(х⁰ср-х)^2/∑Рх(х-хср)^2

η у/х=√∑Рх(у⁰ср-у)^2/∑Ру(у-уср) ^2

Корреляционные отношения равны корню квадратному из отношений вариации, обусловленных влиянием соответственно признака У на Х и наоборот, к общей вариации признака.

Иногда, по аналогии с прямолинейной корреляции, используют коэффициент криволинейной корреляции r η, который равен средней геометрической от η х/у и η у/х. r η=√ η х/у η у/х.

Равенство η х/у =η у/х свидетельствует о близкой к прямолинейной форме связи между признаками.

Степень отклонения реальной зависимости между значениями признаков от прямолинейной количественно характеризуется мерой линейной связи(γ):

γ= r η-r или γ= r η^2-r^2.

45. По выборочным характеристикам можно построить интервал, в котором с той или иной вероятностью находится генеральный параметр. Вероятности, признанные достаточными для уверенного суждения о генеральных параметрах на основании выборочных показателей, называют доверительными.

Понятие о доверительных вероятностях вытекает из принципа, что маловероятные события считаются практически невозможными, а события, вероятность которых близка к единице, принимают за почти достоверные. Обычно в качестве доверительных используют вероятности Р₁=0.95, Р₂=0.99, Р₃=0.999. Определенным значениям вероятностей соответствуют уровни значимости, под которыми понимают разность α=1–Р. Вероятности 0.95 соответствует уровень значимости α₁=0.05 (5%), вероятности 0.99 – α₂=0.01 (1%), вероятности 0.999 – α₃=0.001 (0.1%). Это означает, что при оценке генеральных параметров по выборочным показателям существует риск ошибиться в первом случае 1 раз на 20 испытаний, т.е. в 5% случаев; во втором – 1 раз на 100 испытаний, т.е. в 1% случаев; в третьем – 1 раз на 1000 испытаний, т.е. в 0.1% случаев. Таким образом, уровень значимости обозначает вероятность получения случайного отклонения от установленных с определенной вероятностью результатов. Вероятности, принятые как доверительные, определяют доверительный интервал между ними. На них можно основывать оценку той или иной величины и те границы, в которых она может находиться при разных вероятностях.

Событие считают достоверным, если его доверительная вероятность ≥0,95 или соответственно уровень значимости Р≤ 0,05.

Для различных вероятностей доверительные интервалы будут следующими:

Р₁=0.95 интервал –1.96σ до +1.96σ (рис. 5)

Р₂=0.99 интервал –2.58σ до +2.58σ

Р₃=0.999 интервал –3.03σ до +3.03σ

Доверительным вероятностям соответствуют следующие величины нормированных отклонений:

вероятности Р₁=0.95 соответствует t₁=1.96σ

вероятности Р₂=0.99 соответствует t₂=2.58σ

вероятности Р₃=0.999 соответствует t₃=3.03σ

Выбор того или иного порога доверительной вероятности осуществляют исходя из важности события. Уровень значимости в таком случае – эта та вероятность, которой решено пренебрегать в данной исследовании или явлении.

Этапы становления науки

1этап: Начинается со сбора сведений об объекте , использования накопленных данных.

2этап:классификация и объединение сходных объектов , их начинают группировать

3этап:установление связи и соотношений между биологическими объектами , связь строится из наблюдений.

4этап:Создание математической модели

5:выявление весичины

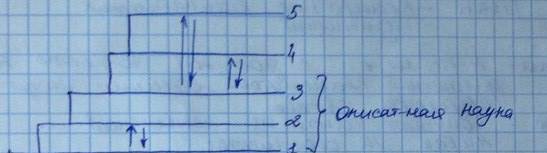
47Статистические совокупности и их классификации:

Наличие вариабельности значений ведет к необходимости при исследовании использовать не отдельные замеры, а их совокупности. Статистическая совокупность является одним из основополагающих понятий биометрии. Совокупность- это система, элементы которой объединены по определенным общим свойствам. В биологии основным системообразующим свойством (точнее, комплексов свойств) является видовая принадлежность. Внутри одновидовой совокупности возможно разграничение на одновозрастные, однополые, обитающие на единой территории и т д совокупности организмов. Разграничение зависит от цели исследования. Например: если изучается возрастная или половая структура вида, то никакой дискриминации при включении особей данного вида в совокупность не производится. Конечный результат определяется не только причинами вероятностного характера, сколько процессами, имеющими биологическую природу.

Формирование совокупности осуществляют из однородных элементов, при фиксированных значениях факторов, о которых известно, что они влияют на величину исследуемого признака (возраст, пол, условия существования). При таком подходе к формированию выборки варьирование значений признака внутри нее будет происходить под влиянием случайных причин; для этого случая разработан математический аппарат статистической обработки.

В конкретную совокупность включают значения одного признака, которые называют единицами совокупности, или вариантами. Количество вариант, входящих в совокупность, определяет ее объем. Если совокупность включает значение признака всех объектов, соответствующих условиям его формирования, то такая совокупность генеральная. Объем генеральной совокупности обозначают буквой N. Совокупность, включающая лишь часть вариант генеральной совокупности называют выборочной или выборкой. Объем выборки обозначают строчной буквой n. В зависимости от него выборки условно подразделяют на малые (n≤30) и большие (n>30). Минимальный объем выборки равен 2.

Статистическая совокупность может быть образована путем многократных замеров значений признака у одного объекта. Если объем, отбираемой от объекта пробы недостаточен для биохимического анализа, приходится объединять пробы от нескольких объектов, в результате чего при смешивании происходит полное сглаживание индивидуальных различий в значениях признака.

48.Способы выравнивания динамического ряда. Способами выравнивания динамического ряда являются: укрупнение периодов, расчет групповой средней, расчет скользящей средней, метод наименьших квадратов

• Укрупнение периодов — применяется, когда явление в интервальном ряду выражено в абсолютных величинах, уровни которых суммируются по более крупным периодам. Применение возможно при кратном числе периодов.
• Вычисление групповой средней — применяется, когда уровни интервального ряда выражены в абсолютных, средних или относительных величинах, которые суммируются, а затем делятся на число слагаемых. Способ применяется при кратном числе периодов.
• Расчет скользящей средней — применяется, когда уровни явлений любого ряда выражены в абсолютных, средних или относительных величинах. Данный метод применяется при наличии некратного числа временных периодов (7, 11, 13, 17, 19) достаточно длинного динамического ряда. Путем вычисления групповой средней значений 3 периодов, а в последующем переходя на определенный уровень и два соседних с ним, осуществляется "скольжение" по периодам. Каждый уровень заменяется на среднюю величину (из данного уровня и двух соседних с ним). Данный метод применяется, когда не требуется особой точности, когда имеется достаточно длинный ряд и можно пренебречь потерей двух значений ряда; в случаях, когда изучается развитие явления под влиянием одного или двух факторов.
• Метод наименьших квадратов применяется для более точной количественной оценки динамики изучаемого явления. Этим способом получаются такие выровненные значения уровней ряда, квадраты отклонений которых от истинных (эмпирических) показателей дают наименьшую сумму.

Наиболее простой и часто встречающейся в практике является линейная зависимость, описываемая уравнением:

У_х = а + вХ, либо У_{теоретич.} = У_{среднее} + вХ,

где У_х — теоретические (расчетные) уровни ряда за каждый период;
а — среднеарифметический показатель уровня ряда, рассчитывается по формуле:
а = ΣУ_факт. / n;
в — параметр прямой, коэффициент, показывающий различие между теоретическими уровнями ряда за смежные периоды, определяется путем расчета по формуле: в = Σ(ХУ_факт)/ ΣХ²
где n — число уровней динамического ряда;
X — временные точки, натуральные числа, проставляемые от середины (центра) ряда в оба конца.

При наличии нечетного ряда уровень, занимающий срединное положение, принимается за 0. Например, при 9 уровнях ряда: -4, -3, -2, -1, 0, +1, +2, +3, +4.

При четном числе уровней ряда две величины, занимающие срединное положение, обозначаются через -1 и +1, а все остальные — через 2 интервала. Например, при 6 уровнях ряда: -5, -3, -1, +1, +3, +5.

Расчеты проводят в следующей последовательности:

1. Представляют фактические уровни динамического ряда (У_ф) (см. табл.).
2. Суммируют фактические уровни ряда и получают сумму У_факт.
3. Находят условные (теоретические) временные точки ряда X, чтобы их сумма (ΣХ) была равна 0.
4. Возводят теоретические временные точки в квадрат и суммируют их, получая ЕX².
5. Рассчитывают произведение Х на У и суммируют, получая ΣХУ.
6. Рассчитывают параметры прямой:
   а = ΣУ_факт / n в = Σ(Х У_факт) / ΣX²
7. Подставляя последовательно в уравнение У_х = а + аУ значения X, находят выровненные уровни У_х.

49. Границы доверия и доверительный интервал.

Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.

Доверительным интервалом параметра θ распределения случайной величины X с уровнем доверия 100%-p^{[примечание 1]}, порождённым выборкой (x₁,…,x_n), называется интервал с границами 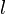(x₁,…,x_n) и 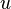(x₁,…,x_n), которые являются реализациями случайных величин L(X₁,…,X_n) и U(X₁,…,X_n), таких, что

.

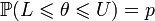Граничные точки доверительного интервала 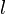и 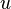называются доверительными пределами.

Интерпретация доверительного интервала, основанная на интуиции, будет следующей: если p велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение θ.^{[ссылка 2]}

Еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра θ, совместимых с опытными данными и не противоречащих им.

Границы доверительного интервала обычно определяются через дисперсию, которая является параметром закона нормального распределения случайных величин

51.

КРИТЕРИЯ ХИ·КВАДРАТ (х2·РАСПРЕДЕЛЕНИЕ Проверку гипотез о законах распределения также произво­ дят с помощью специально выработанных критериев. Один из них, нашедший широкое применение в биометрии,- критерий согласия, или соответствия 2 (предложен в 1900 г. К. Пирсо­ ном). Этот критерий представляет собой сумму квадратов От­ клонений эмпирических частот f от вычисленных или ожидае­ мых частот {', отнесенную к теоретическим частотам, т. Е

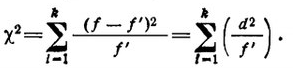Символ Х2 не является квадратом какого-то числа, а выра­жает лишь исходную величину, определяемую данной форму­лой. Буквой d обозначена между эмпирическими и вычисленными частотами. Величина критерия Х2 всегда поло­жительна, так как отклонения эмпири­ческих частот от ожидаемых или вы­ численных частот возведены в квад­рат. Поэтому при определении разно­сти d знаки чисел можно не учиты­вать, вычитая из больших значений меньшие. Распределение вероятных значений случайной величины Х2 является непрерывным и асимметричным, оно зави­сит от числа степеней свободы k и приближается к нормаль­ной кривой по мере увеличения числа испытаний n. Поэтому применение критерия 2 к оценке дискретных распределений сопряжено с некоторыми погрешностями, которые сказываются на его величине, особенно при малых выборках. Для того чтобы оценки были более точными, выборка, рас­пределяемая в вариационный ряд, должна содержать не менее 50 вариант. Поэтому часто считают, что применение критерия Х2 требует, чтобы в крайних классах вариационного ряда со­ держалось не менее пяти вариант. Если в крайних классах со­ держится меньше чем пять вариант, то вычисленные и эмпири­ческие частоты объединяются до указанного минимума и со­ответственно уменьшается число классов вариационного ряда.

Число степеней свободы устанавливают по вторичному числу классов с учетом ограничений свободы вариации, которая в разных случаях бывает различной. Так, при оценке эмпириче­ских распределений, следующих нормальному закону, число степеней свободы k=N-З.

На величине критерия 'Х2 сказывается степень точности, с какой определены теоретически вычисленные или ожидаемые частоты. Поэтому при сопоставлении эмпирических частот с вычисленными частотами последние не следует округлять до целых чисел.

• Асимметрия – Коэффициент асимметрии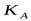характеризует асимметричность («скошенность») распределения признака в совокупности
• Эксцесс– Показатель эксцесса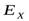представляет собой отклонение вершины эмпирического распределения вверх или вниз («крутость») от вершины кривой нормального распределения

Асимметрия распределения

• При 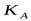=0 распределение считается нормальным.
• При 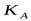> 0 правосторонняя асимметрия.
• При 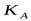<0 левосторонняя асимметрия.
• Если асимметрия более 0,5, то независимо от знака она считается значительной
• Если асимметрия меньше 0,25, то она считается незначительной

Показатель Пирсона зависит от степени асимметричности в средней части ряда распределения, а показатель асимметрии, основанный на моменте третьего порядка, -от крайних значений признака.