Кодирование действительных чисел
Кодирование действительных чисел
Мантисса и порядок
Действительные (вещественные) числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера.
При изображении действительных чисел во многих языках программирования вместо запятой принято ставить точку. Так, например, число 5 — целое, а числа 5.1 и 5.0 — действительные. Для удобства отображения чисел, принимающих значения из достаточно широкого диапазона (то есть, как очень маленьких, так и очень больших), используется форма записи чисел с порядком основания системы счисления. Например, десятичное число 1.75 можно в этой форме представить так:
1.75×10° = 0.175×101 = 0.0175×102 = ...,
или так:
17.5×10–1 = 175.0×10–2 = 1750.0×10–3 = ....
В языках программирования этой записи обычно соответствует запись 1.75E0 = 0.175E1 = 0.0175E2 или 17.5E–1 = 175.0E–2 = 1750.0E–3 = ....
Любое число N в системе счисления с основанием q можно записать в виде
N = М ×qp, (1)
где M называется мантиссой числа, а p — порядком. Такой способ записи чисел называется представлением с плавающей точкой (запятой). Если "плавающая" точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведённых под мантиссу, обеспечивается запись максимального количества значащих цифр числа, то есть максимальная точность представления числа в машине.
Порядок также иногда называют экспонентой или просто показателем степени.
Нормальная и нормализованная форма
Нормальной формой числа с плавающей точкой называется такая форма, в которой мантисса (без учёта знака) в десятичной системе находится на полуинтервале [0; 1). Такая форма записи имеет недостаток: некоторые числа записываются неоднозначно (например, 0,0001 можно записать в 4 формах — 0,0001×100, 0,001×10−1, 0,01×10−2, 0,1×10−3), поэтому распространена также другая форма записи — нормализованная.
В литературе встречаются разные определения нормализованной формы записи. Здесь примем следующее определение:
| В нормализованной форме мантисса числа принимает значения от 1/p (включительно) до 1 (не включительно). То есть m – правильная p-ичная дробь, у которой первая цифра после запятой не равна нулю: 1/p <= m < 1. |
Примеры нормализованного представления:
3,14 = 0.314 * 101
752.15 = 0.75215•103;
- 0.000039 = - 0.39•10-4;
Примеры записи двоичных чисел. Предварительно напомню, что в двоичной системе умножение на два в какой-либо степени – это сдвиг разрядов. Если число умножается на 2 в какой-то степени, и если эта степень – целое положительное число, то это будет сдвиг влево на количество разрядов, которое соответствует степени числа два. Как нетрудно догадаться, деление – это сдвиг вправо.
1 = 0.1 * 21 (сдвинули число влево на один разряд)
100 = 0.1 * 23 (сдвинули число влево на три разряда)
11,11010010 = 0.1111010010 * 22 (сдвинули число влево на два разряда)
0,01 = 0.1 * 2-1 (сдвинули число вправо на один разряд)
В нормализованной форме любое число (кроме 0) записывается единственным образом. Ноль же представить таким образом невозможно, поэтому стандарт предусматривает специальную последовательность битов для задания числа 0 (а заодно и некоторых других полезных чисел, таких как -\infty и +\infty). Так как старший двоичный разряд (целая часть) мантиссы вещественного числа в нормализованном виде всегда равен «1», то его можно не записывать, сэкономив таким образом один бит, что и используется в стандарте IEEE 754.
Типы чисел с плавающей точкой (по IEEE 754)
Познакомиться самостоятельно, например, на Викиконспекте
Особые значения чисел с плавающей точкой
Ноль (со знаком)
Как уже было оговорено выше, в нормализованной форме числа с плавающей точкой невозможно представить ноль. Поэтому для его представления зарезервированы специальные значения мантиссы и порядка - число считается нулём, если все его биты, кроме знакового, равны нулю. При этом в зависимости от значения бита знака ноль может быть как положительным, так и отрицательным.
Арифметика нуля со знаком
Арифметика отрицательного нуля аналогична таковой для любого отрицательного числа и понятна интуитивно. Вот несколько примеров:
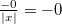(если 
)
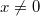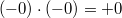
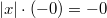
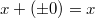
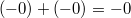
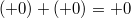
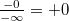
Неопределенность (NaN)
NaN - это аббревиатура от фразы "not a number". NaN является результатом арифметических операций, если во время их выполнения произошла ошибка (примеры см. ниже). В IEEE 754 NaN представлен как число, в котором все двоичные разряды порядка - единицы, а мантисса не нулевая.
| Знак | |||||||||||||||||
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 1, | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | =  | |||||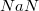
Любая операция с NaN возвращает NaN. При желании в мантиссу можно записывать информацию, которую программа сможет интерпретировать. Стандартом это не оговорено и мантисса чаще всего игнорируется.
Как можно получить NaN?
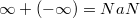
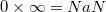
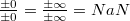
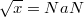, где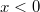 
Есть и другие способы получения NaN, подробности можно найти по ссылкам в соответствующем разделе.
По определению NaN ≠ NaN, поэтому, для проверки значения переменной нужно просто сравнить ее с собой.
Бесконечности
В число с плавающей запятой можно записать значение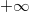 
или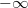 
. Как и нули со знаком, бесконечности позволяют получить хотя бы близкий к правильному результат вычисления в случае переполнения. Согласно стандарту IEEE 754 число с плавающей запятой считается равным бесконечности, если все двоичные разряды его порядка - единицы, а мантисса равна нулю. Знак бесконечности определяется знаковым битом числа.
| Знак | |||||||||||||||||
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 1, | =  | |||||||||||||||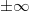
Получить бесконечность можно при переполнении и при делении ненулевого числа на ноль.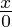 
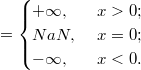
Кодирование действительных чисел
Мантисса и порядок
Действительные (вещественные) числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера.
При изображении действительных чисел во многих языках программирования вместо запятой принято ставить точку. Так, например, число 5 — целое, а числа 5.1 и 5.0 — действительные. Для удобства отображения чисел, принимающих значения из достаточно широкого диапазона (то есть, как очень маленьких, так и очень больших), используется форма записи чисел с порядком основания системы счисления. Например, десятичное число 1.75 можно в этой форме представить так:
1.75×10° = 0.175×101 = 0.0175×102 = ...,
или так:
17.5×10–1 = 175.0×10–2 = 1750.0×10–3 = ....
В языках программирования этой записи обычно соответствует запись 1.75E0 = 0.175E1 = 0.0175E2 или 17.5E–1 = 175.0E–2 = 1750.0E–3 = ....
Любое число N в системе счисления с основанием q можно записать в виде
N = М ×qp, (1)
где M называется мантиссой числа, а p — порядком. Такой способ записи чисел называется представлением с плавающей точкой (запятой). Если "плавающая" точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведённых под мантиссу, обеспечивается запись максимального количества значащих цифр числа, то есть максимальная точность представления числа в машине.
Порядок также иногда называют экспонентой или просто показателем степени.