Основные принципы моделирования
- Дифференциальные уравнения, описывающие процессы для модели и натуры должны быть одинаковы, идентичны – это достаточное условие подобия.
Дифференциальное уравнение не может описывать какой-нибудь единственный процесс, оно описывает бесчисленное множество однородных процессов, класс процессов, в пределах которого действует примененные физические процессы.
- Модель и объект должны быть геометрически подобны.
- Критерии, описывающие физические и геометрические свойства процесса для объекта и модели должно быть равны.
- Начальные и граничные условия для модели и объекта должны бытьодинаковы.
2,3 и 4 принципы моделирования является необходимыми условиями подобия, иногда называемые условиями однозначности.
В основе моделирования процессов лежат методы теории подобия.
Теория подобия– это способ научного обобщения экспериментальных данных.
Она указывает: 1) как нужно вести эксперимент;
2) как обрабатывать данные. Она позволяет при проведении минимального числа опытов обобщить опытные данные всех подобных явлений.
Разберем элементы теории подобия и рассмотрим условия однозначности.
Геометрическое подобие – это подобие геометрической формы и соотношения размеров аппарата, где осуществляется процесс. Признаком подобия геометрических фигур являются частично равные соотношения их характерных размеров.
Приняты обозначения для натуры – один «штрих», для модели – два «штриха» .
РИСУНОК!!!!
- Отношение сходственных величин разных фигур называется константами подобия
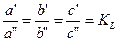
- Отношения каких-то велечин внутри одной фигуры, остающееся такими же идеал. модели, называется инвариантами подобия
 i l=inv=idem “одно и тоже”
i l=inv=idem “одно и тоже”
ke и ie - безразмерные величины. При переходе к новой подобной фигуре константа подобия меняется, а инвариант подобия остается постоянным.
- Инвариант подобия, выраженный посредством величин одной размерности называется симплексом – Г.
a’/b’=l/d=Г– симплекс геометрического подобия
- Инвариант подобия, выраженный отношением велечины разной размерности называется критерием подобия.
Например: для движения жидкости по трубопроводу 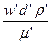 =
= 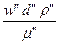 =i=Re
=i=Re
Все Kе, i, Г и критерии – безразмерные величины
Для соблюдения условий однозначности кроме геометрического подобия необходимо так же подобие полей физических величин, начальных и граничных условий, а так же временное подобие.
Временное подобие – называют гомохронностью (однородностью во времени).
Пусть τ’ и τ’’ – общая продолжительность ХТ процесса, и τ’=2, τ’’=1.
Оно складывается в общем случае из ряда промежуточных операций: загрузки, реакций, охлаждение, разгрузки аппарата.
τ1’, τ1’’; τ2’, τ2’’; τ3’, τ3’’; τ4’, τ4’’.
Временное подобие определяется как

 =
=  ….. Kτ=2 константа временного подобия
….. Kτ=2 константа временного подобия
Если Кτ=1 – процесс синхронный.
Подобие полей физических величин – для сходственных точек обеих подобных систем отношения физических свойств (ρ, μ, с, t, и др.) должны быть постоянными.
Напр. для плотности
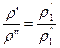 =
= 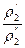 =K
=K  – константы подобия плотности.
– константы подобия плотности.
Или для вязкости
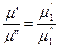 =
=  =K
=K 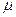 – константы подобия полей вязкости.
– константы подобия полей вязкости.
Подобие начальных и граничных условий предполагает, что отношения основных параметров в начале и на границе для объекта и модели являются величинами постоянными.
Подобные преобразования уравнения
Навье-Стокса
Как уже говорилось, уравнение Н-Стокса не решается аналитически применительно к задачам турбулентных течений, поэтому не удается теоретически получить расчет вне зависимости для определения потерь энергии (напора). Поэтому приведем их подобные преобразования.
Запишем уравнение Н-Стокса для оси z
- 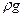 +
+ 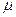 Ñ2wz -
Ñ2wz -  =
= 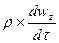 (1)
(1)
Распишем оператор Лапласа, силу инерции, разделим (1) на ρ и запишем уравнение Н-стокса для изменения только вдоль оси х, где V=μ/ρ
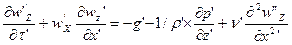 (2)
(2)
Это уравнение для натуры. Запишем для модели
 По достаточным условием подобие ???? уравнения для натуры и модели д.б. равны, т.е. (2)=(3)
По достаточным условием подобие ???? уравнения для натуры и модели д.б. равны, т.е. (2)=(3)
В соответствии с необходимыми условиями подобия все константы для модели и натуры д.б. одинаковы и можем записать
K τ= τ’/ τ” Кg=g’/g” Kl=l’/l” Kp=p’/p” (4)
Мы должны выразить уравнение натуры (2) через модель, подставляя следующее выражение (5)
τ’=K*τ” g’=Kg*g” l’=Kl*l” p’=Kp*p”(5)
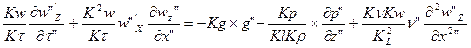
По достаточным условиям (6) д.б = (3), а это возможно, если коэффициенты в уравнении (6) равны
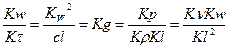
Распишем 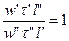 или
или 
1) Но – критерий гомохронности-временное подобие, характер неустановившейся процесс в гидродинамике
Рассмотрим вторую пару
2)Kw2 / Kl=Kg и получим w2/lg=Fr – критерий Фруда
Характеризует соотношение силы инерции и силы тяжести в подобных системах.
Все соотносим с силой инерции !!!
Kw2 / Kl=Kp/K  Kl : (Kw2)
Kl : (Kw2)
3)DP/  w2=Eu критерий Эйлера– характеризует соотношение м/у силой давления и силой инерции в подобных системах
w2=Eu критерий Эйлера– характеризует соотношение м/у силой давления и силой инерции в подобных системах
Kw2 / Kl= 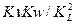
4) 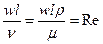 критерий Рейнольдса –характеризует отношение сил инерции к силе трения.
критерий Рейнольдса –характеризует отношение сил инерции к силе трения.
Кроме 4ех основных критериев существуют вспомогательные (путем ХМ:)
У Fr 3 аналога
Галилея 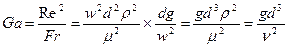
Архимеда 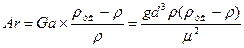
Грисгофа Gr=Ga * 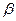 *Dt– для описания тепловых процессов.
*Dt– для описания тепловых процессов.
Теоремы подобия
I Теорема
Критерии описывающие процесс для натуры и модели должны быть численно равны.
Теорема ставит вопрос: как построить модель и какие величины измерить при проведении опыта.
Ответ: чтобы критерии для модели и натуры были одинаковы измерить те величины, которые входят в критерии.
II Теорема (Бэкингема)
Решение любого ????? уравнения, связывающего между собой переменные, влияющие на процесс, может быть представлено в виде функциональной зависимости между критериями подобия f(Но, Ke, Fr, Eu)=0.
III Теорема (Кирпичева и Тухмана)
I формулировка – Явление подобны, если соблюдаются достаточные и необходимые условия подобия.
II формулировка – Определяющие критерии для натуры и модели д.б. равны.
Определяющие критерии составлены из физических величин, входящих в условии однородности
Определяемые – содержат искомые величины
Так, в любом гидродинамическом процессе главное – перепад давления
Eu = f(Но, Fr, Re)
