Равномерная сходимость и интегрируемость предельной функции функциональной последовательности и суммы функционального ряда

Иванов В.И.

профессор, д.ф.-м.н.

КОНСПЕКТ ЛЕКЦИЙ

по дисциплине

Математический анализ

(Часть 4)

Направление подготовки: 010400 «Прикладная математика и информатика»

Профиль подготовки: «Прикладная математика и информатика»

Форма обучения: очная

Тула 2013 г.

Рассмотрено на заседании кафедры

протокол № 1 от 02 сентября 2013 г.

Зав. кафедрой________________В.И. Иванов

СОДЕРЖАНИЕ

ЛЕКЦИЯ 1. Поточечная и равномерная сходимости функциональной последовательности и функционального ряда. Критерий Коши равномерной сходимости. Признаки Вейерштрасса, Абеля, Дирихле равномерной сходимости функционального ряда. 4

ЛЕКЦИЯ 2. Равномерная сходимость и непрерывность предельной функции функциональной последовательности и суммы функционального ряда. Пространство 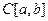. Его полнота. 9

ЛЕКЦИЯ 3. Равномерная сходимость и интегрируемость предельной функции функциональной последовательности и суммы функционального ряда. 11

ЛЕКЦИЯ 4. Равномерная сходимость и дифференцируемость предельной функции функциональной последовательности и суммы функционального ряда. Пространство 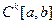. Его полнота. 13

ЛЕКЦИЯ 5. Степенные ряды. Поточечная сходимость. Радиус и интервал сходимости. Формула Коши-Адамара. 14

ЛЕКЦИЯ 6. Равномерная сходимость степенного ряда. Свойства суммы степенного ряда. 16

ЛЕКЦИЯ 7. Ряд Тейлора. Единственность разложения функции в степенной ряд. Достаточное условие разложимости. Ряд Тейлора-Маклорена для функций 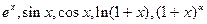................................................... 18

ЛЕКЦИЯ 8. Собственные интегралы, зависящие от параметра. Теоремы о его непрерывности, интегрируемости и дифференцируемости. 20

ЛЕКЦИЯ 9. Равномерная сходимость несобственного интеграла, зависящего от параметра. Критерий Коши. Признаки Вейерштрасса, Абеля, Дирихле. 22

ЛЕКЦИЯ 10. Теоремы о непрерывности, интегрируемости и дифференцируемости несобственного интеграла, зависящего от параметра. 26

ЛЕКЦИЯ 11. Гамма и бета-функция Эйлера. Формула Стирлинга. 28

ЛЕКЦИЯ 12. Евклидово пространство интегрируемых функций. Ортонормированная система. Задача о наилучшем приближении элемента евклидова пространства по ортонормированной системе. Базисность и замкнутость ортонормированной системы. Ряд и коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля. 34

ЛЕКЦИЯ 13. Тригонометрическая система. Ее замкнутость. Тригонометрические ряды Фурье интегрируемых функций. Сходимость в среднеквадратичном. Равенство Парсеваля. 38

ЛЕКЦИЯ 14. Тригонометрические ряды Фурье непрерывных функций. Частичные суммы. Ядро Дирихле. Отсутствие равномерной сходимости. Достаточное условие равномерной сходимости. 43

ЛЕКЦИЯ 15. Равномерная сходимость средних Фейера для непрерывных функций. Теоремы Вейерштрасса о равномерном приближении непрерывных функций тригонометрическими полиномами и алгебраическими многочленами. Теорема Стоуна-Вейерштрасса. 46

ЛЕКЦИЯ 16. Достаточное условие поточечной сходимости тригонометрического ряда Фурье. 50

ЛЕКЦИЯ 17. Преобразование Фурье. Косинус и синус преобразования Фурье. Свойства преобразования Фурье. Обратное преобразование Фурье. 54

ЛЕКЦИЯ 1

Поточечная и равномерная сходимости функциональной последовательности и функционального ряда. Критерий Коши равномерной сходимости. Признаки Вейерштрасса, Абеля, Дирихле равномерной сходимости функционального ряда

1. Поточечная и равномерная сходимости функциональной последовательности и функционального ряда

Сумма геометрической прогрессии 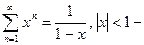сходится и определяет новую функцию. Это есть пример функционального ряда.

Пусть 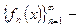последовательность функций, определённых на одном и том же множестве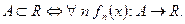

Функциональный ряд – это ряд вида .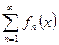

Определим область сходимости (поточечной сходимости) для функциональной последовательности и функционального ряда: 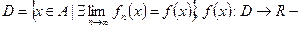предельная функция. Аналогично для функционального ряда 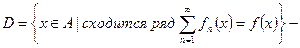область сходимости (поточечной сходимости) функционального ряда, а 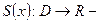сумма функционального ряда.

Нас будут интересовать следующие три задачи.

Задача 1. Пусть последовательность функций 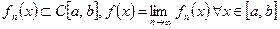. Когда .

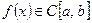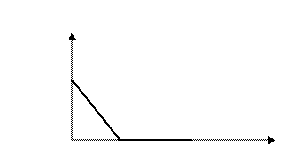Примеры. Пусть .

.

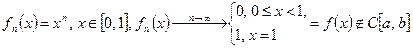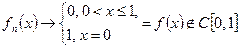Аналогичную задачу можно поставить и для функционального ряда.

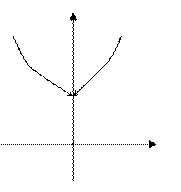Пример. .

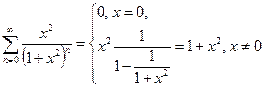Задача 2. Пусть 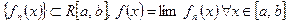(R – интегрируема). Когда можно гарантировать, что 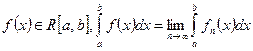или .

.

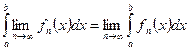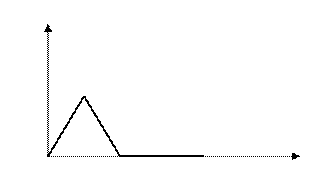
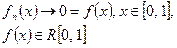
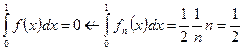Задача 3. Пусть 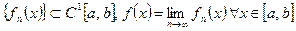(С¹- непрерывно дифференцируема). Когда 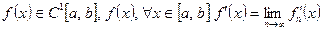, или .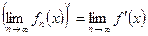

Пример. .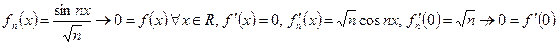

Итак, в результате поточечной сходимости предельная функция не наследует хорошие свойства функции последовательности. Необходимо усиление поточечной сходимости. Таким усилением будет равномерная сходимость.

Равномерная сходимость последовательности функций и функционального ряда

Вначале проанализируем условие поточечной сходимости последовательности функций на отрезке: 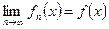на .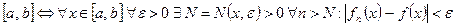

Будем говорить, что последовательность 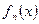равномерно сходится на 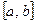к f(x), т.е. 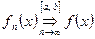, если .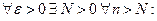

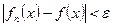Пусть 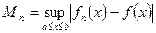, тогда эквивалентное определение равномерной сходимости выглядит так: .

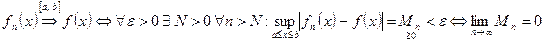Ряд 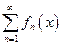называется равномерно сходящимся к своей сумма на [a, b], если его последовательность частичных сумм сходится равномерно на [a, b] к S(x), т.е. 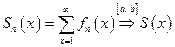или

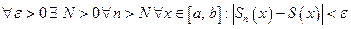
Из равномерной сходимости вытекает поточечная сходимость, а обратное - неверно. Рассмотрим примеры.

Пример 1.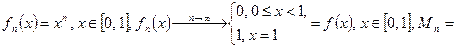

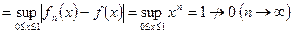, т.е. поточечная сходимость есть, а равномерной сходимости нет.

Пример 2.

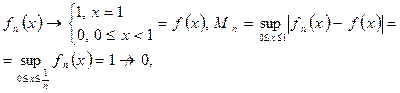
т.е. равномерной сходимости нет.

Пример 3.

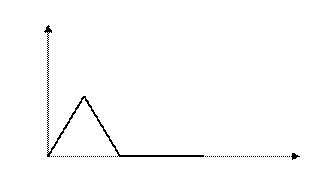
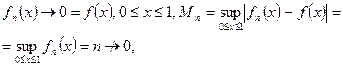
т.е. равномерной сходимости нет.

Пример 4.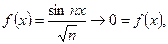

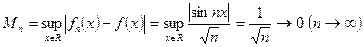т.е. равномерная сходимость есть, но и в этом случае её недостаточно.

2. Критерий Коши равномерной сходимости. Признак Вейерштрасса равномерной сходимости функционального ряда

Критерий Коши.

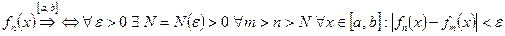, или .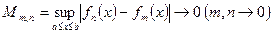

Критерий Коши также называется равномерной фундаментальностью.

Доказательство.Необходимость.

Пусть 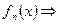, тогда

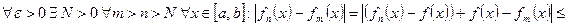
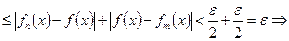равномерная фундаментальность последовательности f_n(x).

Достаточность.

Пусть f_n(x) – равномерная фундаментальная последовательность Þ f_n(x) – фундаментальная 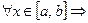(по критерию Коши) 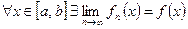. Запишем подробно условие равномерной фундаментальности: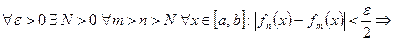

.

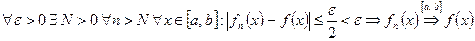Доказано.

Для функционального ряда критерий Коши выглядит так: 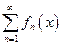равномерно сходится на [a, b] тогда и только тогда, когда последовательность частичных сумм S_n(x) равномерно фундаментальная на [a, b], т.е. .

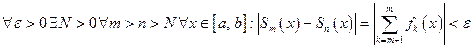Пример.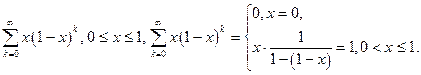

Применим критерий Коши: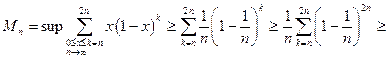

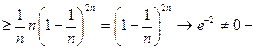равномерной сходимости нет.

Для равномерной сходимости функционального ряда можно указать некоторые достаточные признаки.

Признак Вейерштрасса.

Если 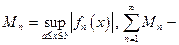сходится, то 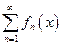сходится равномерно на [a, b].

Доказательство.Будем использовать критерий Коши для равномерной сходимости функционального ряда.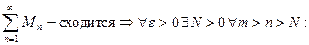

(по критерию Коши)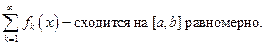

Доказано.

Пример.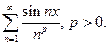

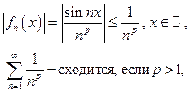
поэтому при 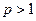по признаку Вейерштрасса функциональный ряд сходится равномерно для всех 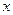, хотя поточечно он сходится при .

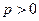При 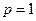можно показать, что для ряда 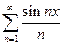справедливо следующее важное утверждение: частичные суммы ряда 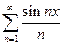равномерно ограничены для любого х: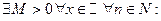

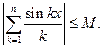
Доказательство.В силу периодичности и нечётности достаточно считать и рассмотреть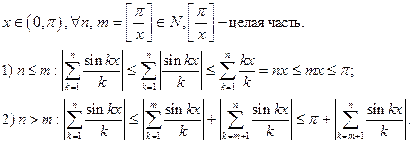

Для оценки 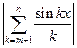воспользуемся преобразованием Абеля:

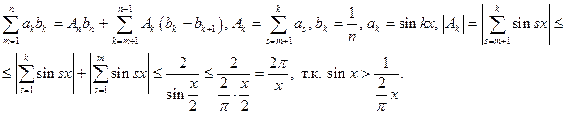
Далее:

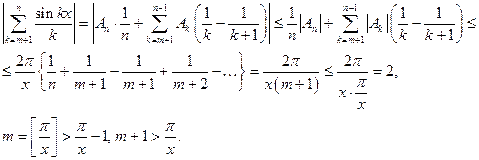
Итак,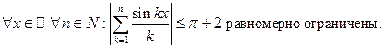

3. Признаки Абеля, Дирихле равномерной сходимости функционального ряда

Сформулируем признаки равномерной сходимости Дирихле и Абеля для рядов вида: 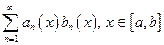(1).

Признак Дирихле.

Если для ряда (1) выполнены условия:

1)

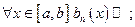
2)

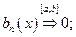
3)

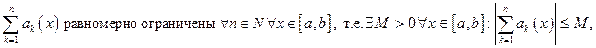
то ряд (1) сходится равномерно на [a, b].

Признак Абеля.

Если для ряда (1) выполнены условия:

1)

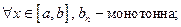
2)

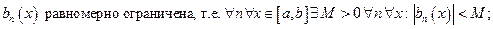
3) 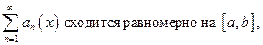то ряд (1) сходится равномерно на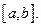

Эти признаки доказываются точно также как и для числовых рядов, используя преобразование Абеля и критерий Коши для сходящихся рядов.

Задача. При каких условиях на 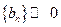(невозрастающая)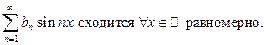

Достаточные условия вытекают из признака Дирихле:

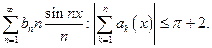
Остаётся проанализировать условия (1) и (2) и потребовать, чтобы 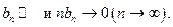Если эти условия выполнены, то ряд сходится равномерно. Можно показать, что эти условия являются и необходимыми.

ЛЕКЦИЯ 2

Равномерная сходимость и непрерывность предельной функции функциональной последовательности и суммы функционального ряда. Пространство 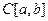. Его полнота

1. Равномерная сходимость и непрерывность предельной функции функциональной последовательности

Теорема 1.Если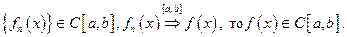

Доказательство.Будем исходить из следующей оценки:

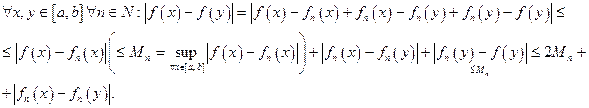
Итак,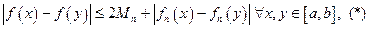

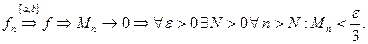Зафиксируем 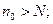функция 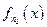Î

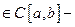равномерно непрерывна на [a, b]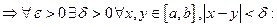

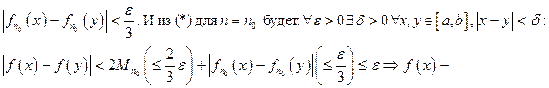
равномерно непрерывна на [a, b].

Доказано.

2. Равномерная сходимость и непрерывность суммы функционального ряда

Теорема 1¢.Если 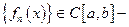непрерывна, функциональный ряд 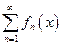сходится к 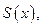то

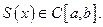
Доказательство.Если 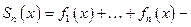частичные суммы, то 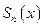также непрерывны и равномерно сходятся к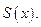

Утверждение теоремы 1¢ вытекает из теоремы 1.

Доказано.

3. Пространство 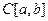. Его полнота

Множество непрерывных функций на отрезке 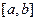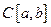- линейное пространство бесконечной размерности, в котором можно ввести норму 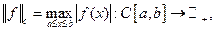для которой выполнены свойства:

1)

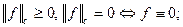
2)

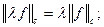
3)

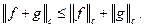
Линейное пространство с нормой называется нормированным пространством.

Норма позволяет определить сходимость на [a, b]:

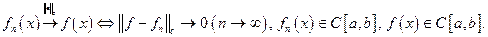
Последовательность функций называется фундаментальной, если 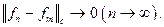Нормированное пространство, в котором всякая фундаментальная последовательность является сходящейся, называется полным, или банаховым пространством (по имени С. Банаха).

Отметим, что всякая сходящаяся последовательность является фундаментальной, т.е. в полном пространстве сходимость эквивалентна фундаментальности, или в полном пространстве выполнен критерий Коши.

Покажем, что нормированное пространство 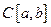является полным. Для этого рассмотрим сходимость в нём:

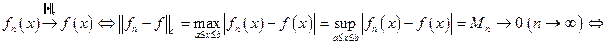
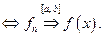
Итак, сходимость по норме пространства 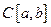эквивалентна равномерной сходимости. Известно, что для равномерной сходимости выполнен критерий Коши. Это и означает, что пространство 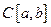- полное.

ЛЕКЦИЯ 3

ЛЕКЦИЯ 4

Равномерная сходимость и дифференцируемость предельной функции функциональной последовательности и суммы функционального ряда. Пространство 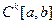. Его полнота

1. Равномерная сходимость и дифференцируемость предельной функции функциональной последовательности

Теорема 3.Если

1)

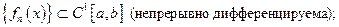
2)

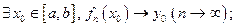
3)

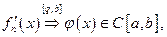
то 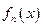также равномерно сходится к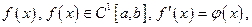

.

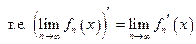Доказательство.Будем пользоваться следующими критерием:

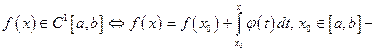произвольное, а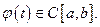

Далее пользуясь критерием Коши, покажем равномерную сходимость последовательности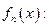

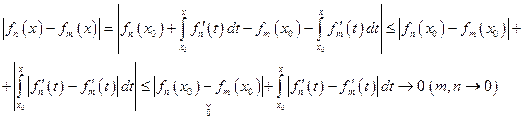
равномерно по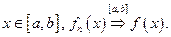

Далее:

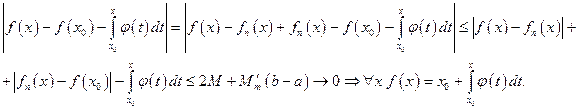
Доказано.

2. Равномерная сходимость и дифференцируемость суммы

функционального ряда

Теорема 3¢.Если

1)

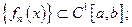
2)

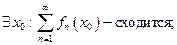
3)

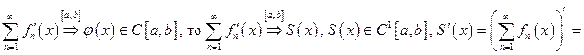
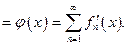
Доказательство.Если 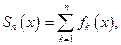то

1)

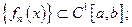
2)

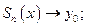
3)

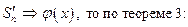
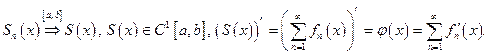
Доказано.

3. Пространство 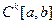. Его полнота

Пространство 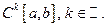- это множество 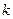раз непрерывно дифференцируемых на отрезке 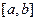функций. Это линейное пространство, в котором можно ввести норму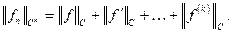

Охарактеризуем сходимость в этом пространстве:

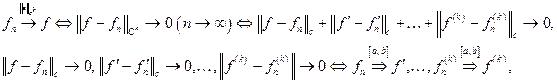
т.е. сходимость по норме пространства 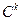эквивалентна равномерной сходимости самой последовательности и последовательности её производных до порядка k включительно.

Отметим, что пространство 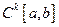также является полным.

ЛЕКЦИЯ 5

ЛЕКЦИЯ 6

ЛЕКЦИЯ 7

Ряд Тейлора. Единственность разложения функции в степенной ряд. Достаточное условие разложимости. Ряд Тейлора-Маклорена для функций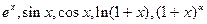

1. Ряд Тейлора. Единственность разложения функции в степенной ряд

Если функция раскладывается в степенной ряд (1) в некоторой окрестности точки а, то эта функция является бесконечно дифференцируемой в этой окрестности.

Пример.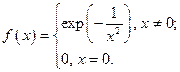

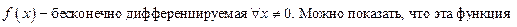непрерывна и имеет производные любого порядка и при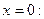

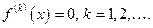
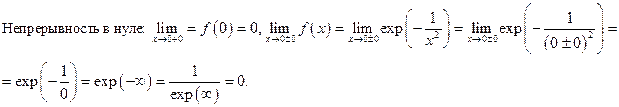
Производная в нуле: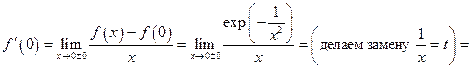

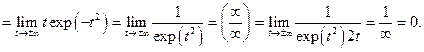
Теорема (о единственности разложения функции в степенной ряд).Если в некоторой окрестности точки а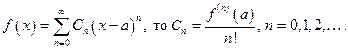

Степенной ряд вида 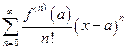называется рядом Тейлора в окрестности точки а.

Таким образом, если функция раскладывается в степенной ряд, то он является рядом Тейлора. Например: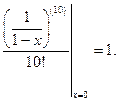

Доказательство.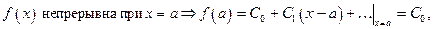

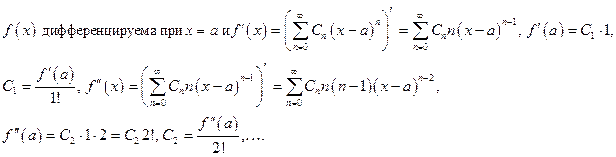
Доказано.

Вернёмся к предыдущему примеру. Если ранее введённая функция раскладывается в степенной ряд в некоторой окрестности точки противоречие с возможностью разложения некоторой функции в некоторой окрестности. Т.е. одной бесконечной дифференцируемости функции недостаточно для разложения в ряд.

2. Достаточное условие разложимости

Исследуем условия разложимости функции в степенной ряд. Для этого воспользуемся формулой Тейлора:

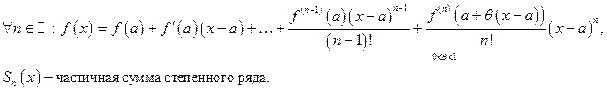
Отсюда, 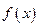раскладывается в степенной ряд в точке а тогда и только тогда, когда:

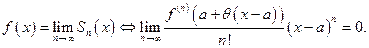Таким образом, вопрос о разложимости связан с ростом производных функции f. Укажем достаточные условия на рост производных для разложимости функций в степенной ряд.

Теорема.Если 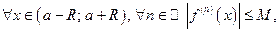то

.

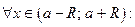
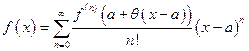Доказательство.Имеем

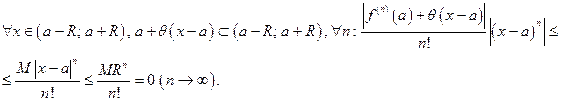
Убедимся, что 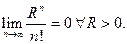Удобнее всего для этого рассмотреть ряд 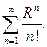и доказать его сходимость По признаку Даламбера получаем:

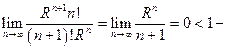ряд сходится, и в таком случае предел общего члена равен нулю.

Доказано.

3. Ряд Тейлора-Маклорена для элементарных функций

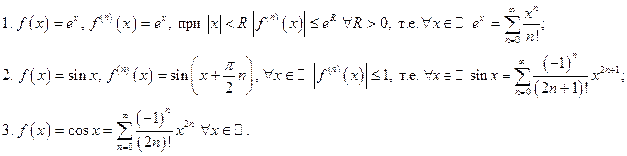
Последнее разложение получено почленным дифференцированием предыдущего разложения.

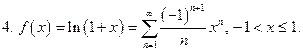
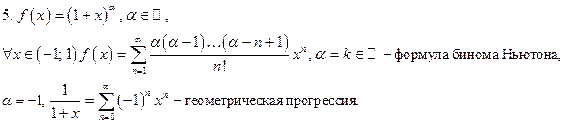
ЛЕКЦИЯ 8

ЛЕКЦИЯ 9

ЛЕКЦИЯ 10

ЛЕКЦИЯ 11

Доказательство.

1. Т.к.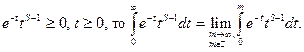

2.

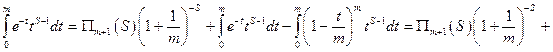
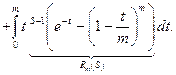
Из этого представления равенство (*) будет вытекать тогда и только тогда, когда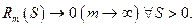

3. Введём вспомогательные неравенства.

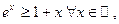
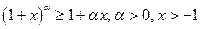(неравенство Бернулли).

Докажем это неравенство методом математической индукции.

При 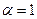равенство очевидно.

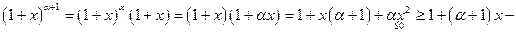верно.

4. Докажем, что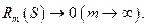

Докажем, что 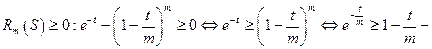неравенство из 3. при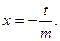

Оценим снизу:

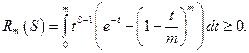
Оценка сверху:

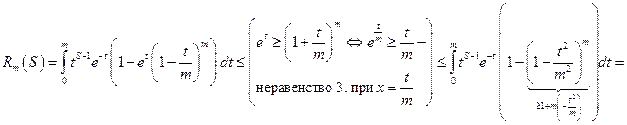
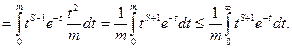
Итак,

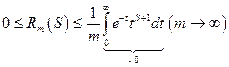и по теореме «о двух милиционерах»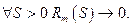

Доказано.

Лемма 1.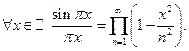

(подробно это доказывается в курсе теории функций комплексного переменного)

Формула дополнения для гамма-функции

Лемма 2. 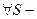нецелого справедливо следующая формула дополнения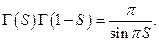

В частности, при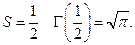

Доказательство.Имеем по формуле Эйлера

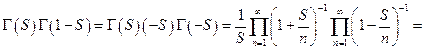
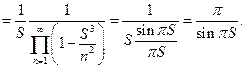
Доказано.

Задача. Вычислить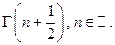

Пр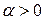и и 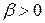бета-функция Эйлера 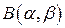задается равенством:

.

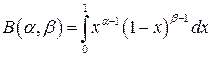Подынтегральная функция имеет, вообще говоря, две особенности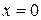: при и при 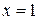, поэтому представим интеграл в виде:

.

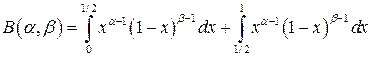Сравнивая первый интеграл в правой части с интегралом 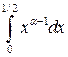, а второй – с 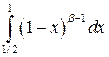, которые сходятся соответственно пр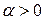и и 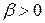и соответственно расходятся при выполнении неравенств 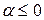и 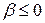, получаем, что областью определения бета-функции в плоскости 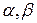является прямой угол , .

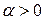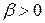Из свойств бета-функции 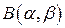укажем следующие:

1) Для любых 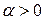и : .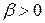

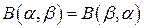2) Для любых 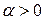и :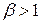

.

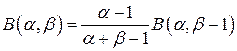3) Для любых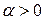

,

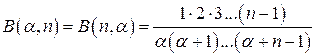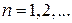
Теорема. Для 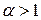и 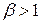справедлива формула

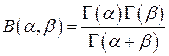. (1)

Замечание. Поскольку гамма - функция 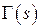определена при всех 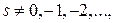то формула (1) в теореме 6 позволяет распространить определение функции 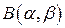на все множество вещественных значений 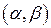, за исключением точек 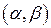, где либо величина 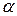, либо величи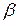на равна .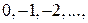

2. Формула Стирлинга

Изучение эйлеровских интегралов завершаем важ­ной для приложений формулой Стирлинга, дающей приближенное значение для гамма-функции или для функции 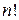при больших значениях аргумента.

Теорема(формула Стирлинга). При 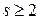имеет место равенство:

,

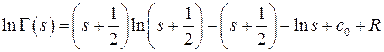где 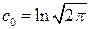, а для величины остатка R выполняются неравенства

.

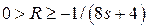Отметим, что если воспользоваться соотношением

,

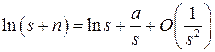то из теоремы 1 можно получить еще один вариант формулы Стирлинга вида:

.

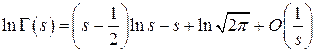В частности, при 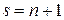отсюда имеем

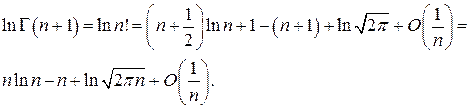
Следовательно, справедлива асимптотическая формула

,

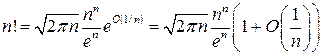которая также называется формулой Стирлинга. Более тщательные вычисления позволяют получить оценку вида 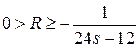для остатка R в асимптотической формуле теоремы. Этот результат был установлен Гауссом. Он же доказал, что величину 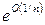в асимптотической формуле для 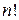можно заменить на 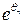, где .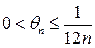

ЛЕКЦИЯ 12

Евклидово пространство интегрируемых функций. Ортонормированная система. Задача о наилучшем приближении элемента евклидова пространства по ортонормированной системе. Базисность и замкнутость ортонормированной системы. Ряд и коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля

1. Евклидово пространство интегрируемых функций

Пусть 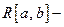линейное пространство интегрируемых по Риману на отрезке [a, b] функций. В нём можно определить скалярное произведение: 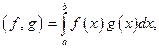удовлетворяющее следующим аксиомам скалярного произведения:

1) 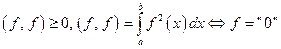(нулевая функция – функция, принимающая нулевые значения в точках непрерывности и возможно положительные значения в точках разрыва, мера которых равна нулю, т.е. нулевая функция – это не одна, а целый класс функций).

2)

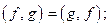
3)

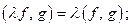
4)

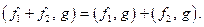
Линейное пространство со скалярным произведением называется Евклидовым пространством. Евклидово пространство можно рассматривать как нормированное, в котором норма определяется по правилам: 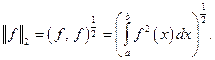Для такого отображения выполнены все аксиомы нормы:

1)

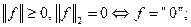
2)

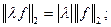
3) 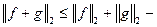неравенство треугольника, и оно легко выводится из неравенства Коши-Буняковского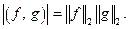

В свою очередь неравенство Коши-Буняковского позволяет определить и угол между функциями: 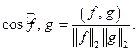В частности, 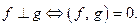Норма позволяет определить расстояние между функциями и сходимость последовательности функций: 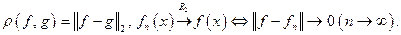Такую сходимость называют среднеквадратичной сходимостью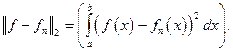

Сравним равномерную сходимость и среднеквадратичную сходимости на отрезке [a, b]. Из равномерной сходимости вытекает среднеквадратичная сходимость:

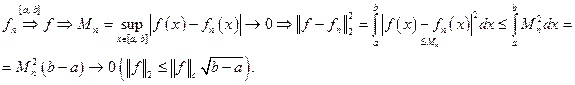
Обратное неверно.

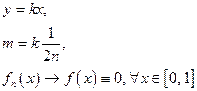
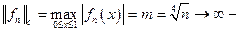равномерной сходимости нет.

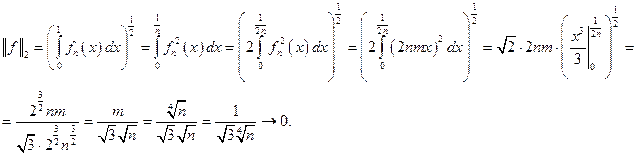
Пространство является бесконечномерным. В нём линейно-независимую систему, например, образуют функции 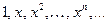(система степеней).

Задача. Охарактеризовать мощность пространства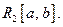

2. Ортонормированная система. Задача о наилучшем приближении элемента евклидова пространства по ортонормированной системе

Счётная система функций 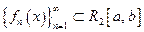называется ортогональной, если 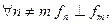и ортонормированной, если система ортогональная и нормированная, т.е. 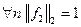. Далее будем обозначать ОС – ортогональная система, ОНС – ортонормированная система.

Рассмотрим задачу о наилучшем среднеквадратичном приближении функции по ОНС.

Пусть 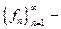ОНС. Линейные комбинации вида 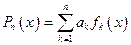будем называть полиномами порядка n по этой ОНС. Множество всех таких полиномов порядка n будет образовывать линейное подпространство 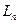размерности п, т.е. 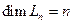, с базисом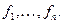

Задача. Доказать, что ОНС – линейно-независимая система.

Для 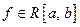величина 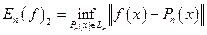называется величиной наилучшего среднеквадратичного приближения функции f полиномами порядка п по нашей ОНС. Полином 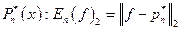называется полиномом наилучшего среднеквадратичного приближения

Теорема. 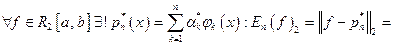причём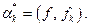

Доказательство. 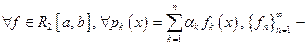ОНС,

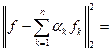
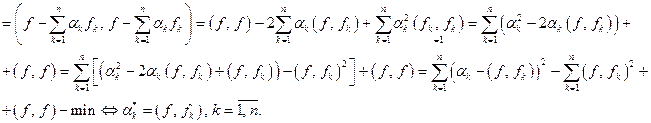Итак, 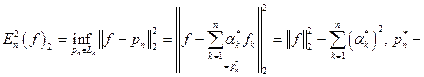единственен.

Доказано.

3. Ряд и коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля. Базисность и замкнутость ортонормированной системы

Если 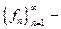ОНС, 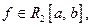то функциональный ряд 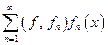называется рядом Фурье функции f по ортонормированной системе 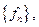а коэффициенты этого ряда называются коэффициентами Фурье.

Частичные суммы ряда Фурье обладают экстремальным свойством: они являются полиномамими наилучшего среднеквадратичного приближения:

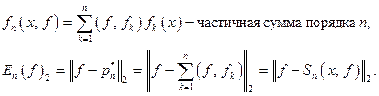
Итак, каждой функции из 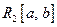можно поставить в соответствие её ряд Фурье. Какое отношение этот ряд Фурье имеет к функции?

Когда этот ряд в среднеквадратичном сходится к функции: 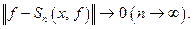Ответы на эти вопросы зависят от свойств ОНС.

Имеем: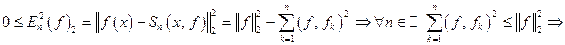

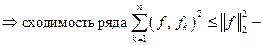неравенство Бесселя.

ОНС 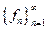называется базисом в 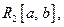если 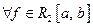её ряд Фурье в среднеквадратичном сходится к ней, т.е. можно записать равенство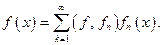

ОНС 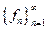называется замкнутой в 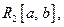если множество всех полиномов по система плотно в 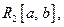относительно среднеквадратичной сходимости, т.е.:

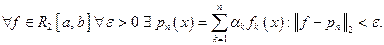
ОНС 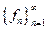называется полной в 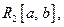если не существует в 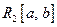ненулевой функции, ортогональной всем функциям системы.

ОНС 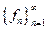удовлетворяет равенству Парсеваля, если 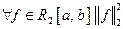равна сумме квадратов коэффициентов Фурье, т.е.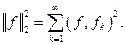

Теорема.Все четыре услови