Методика изучения темы: «Перпендикулярность прямых и плоскостей» в школьном курсе геометрии.
Тему разделить на три части: перпендикулярность прямых в пространстве; перпендикулярность прямой и плоскости; перпендикулярность плоскостей. По каждой из этих частей проводится учет знаний учащихся: сам. работы, к. р., опрос учащихся на уроке и др. В процессе изучения исходить из общей схемы взаимного расположения прямых и плоскостей в пространстве, с которой учащиеся познакомились в начале курса стереометрии при изучении параллельности в пространстве. Особое внимание следует уделить решению задач (надо использовать многогранники – призмы и пирамиды) Особо выделить задачи, решаемые с помощью векторного аппарата, а также задачи, решаемые по готовому рисунку устно. Основная цель: сообщить учащимся основные факты об одном из наиболее важных отношений между прямыми и плоскостями – перпендикулярности; ввести понятие углов между прямыми и плоскостями, между плоскостями. Данная тема изучается в 10 классе.
Перпендикулярность прямых в пространстве.Этот раздел рассматривается как повторение пройденного ранее. Повторение нужно вести по следующему плану:- определение взаимно перпендикулярных прямых:- пересекающиеся и скрещивающиеся взаимно перпендикулярные прямые;- иллюстрация их на моделях многогранников и в окружающей действительности. важно -в пространстве взаимно перпендикулярные прямые могут не иметь общих точек.
Перпендикулярность прямой и плоскости.Изучение начать с повторения о взаимном расположении прямой и плоскости в пространстве. Встает вопрос, в каком случае прямая, пересекающая плоскость будет ей перпендикулярна. Положение «если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой на этой плоскости» иллюстрируется на наглядном пособии на модели прямой призмы. Дается определение перпендикулярности прямой и плоскости в пространстве, их пересечения. Учащимся важно показать на наглядном пособии, что прямая, перпендикулярная двум параллельным прямым, лежащим в плоскости, может оказаться не перпендикулярной плоскости. В итоге этой работы формируется теорема, которая получила название признака перпендикулярности прямой и плоскости (теорема о двух перпендикулярах), и ее доказательство проводится в классе учителем и сопровождается продуманными записями. Изучение взаимосвязи перпендикулярности прямой и плоскости с параллельностью прямых и плоскостей в пространстве следует связать с повторением темы «Параллельность в пространстве».
Перпендикулярность плоскостей.Целесообразно начать с повторения о взаимном расположении двух плоскостей. С помощью рисунков, опираясь на жизненные представления учащихся, выясняется, что две перпендикулярные плоскости являются пересекающимися. В процессе изучения отрабатываются такие вопросы, как:а) определение перпендикулярных плоскостей;б) признак перпендикулярности плоскостей (его доказательство);в) построение перпендикулярных плоскостей;
г) решение задач с использованием определения и признака перпендикулярности плоскостей.
Эти вопросы должны быть центральными в процессе контроля знаний учащихся: при устном опросе, в процессе решения задач в классе и дома, при составлении самостоятельных и контрольных работ для учащихся.
Учебники: 1) Геометрия: учеб.для 10-11кл.сред.шк./Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев. В этом учебнике тема дана в виде главы. В нее входят 3 параграфа. В каждом параграфе даются под пункты. После каждого параграфа даются задачи.
2) Геометрия: учеб.для 7-11кл. сред.шк./Погорелов. В этом учебнике тема дана в виде параграфа. В конце параграфа идут контрольные вопросы, а после идут задачи.
3) Геометрия: 10-11кл.: учебник для общеобразовательных учебных заведений./Шарыгин и др.В этом учебнике дается в виде нескольких параграфов. После Двугранный угол между плоскостями.
7.7 Движения плоскости. Классификация движений. Группа движений и ее подгруппы. Обучение решению задач с помощью геометрических преобразований.
Опр1.Говорят, что преобразование пл-ти 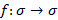 сохраняет расстояние если любая
сохраняет расстояние если любая 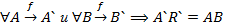
Опр2.Движением пл-ти 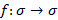 называют преобразование пл-ти сохраняющие расст-ие.
называют преобразование пл-ти сохраняющие расст-ие.
Свойства движения:1)Т.Два движения f и g, выполненные последовательно, дают снова движение.
Док-во: 1. Возьмём произвольные две точки плоскости X и Y, тогда движение f переводит Х в точку Х`, Y в точку Y`, при этом сохраняются расстояния: XY=X`Y`.2. Движение g переводит точки X`в X`` и Y` в Y``, при этом X`Y`=X``Y``.Тогда если выполнить послед-но два движения f и g, то точка Х перейдет в точку Х`` и точка Y – в точкуY``, при этом XY=X`Y`= X``Y``=a, т.е. получим движение.
2) Преобразование, обратное движению, также является движением.
3) При движении прямая переходит в прямую, луч- в луч, отрезок – в отрезок, при этом сохраняться порядок взаимного расположения точек, полуплоскость переходит в полуплоскость.
4) Если 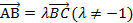 , то при движении f точка А переходит в А`, точка B- в точку B`, точка С в точку С, и при этом
, то при движении f точка А переходит в А`, точка B- в точку B`, точка С в точку С, и при этом 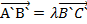 (сохр-ся отн-ие соотв-х отрезков). Следов-но, середина отрезка при движении переходит в середину отрезка.
(сохр-ся отн-ие соотв-х отрезков). Следов-но, середина отрезка при движении переходит в середину отрезка.
5) Движение переводит угол в равный ему угол. След-но, взаимно перпендикулярные прямые переходят во взаимнопер-е прямые.
6)Движение парал-е прямые переводит в параллельные прямые.
Виды движений:тождественное преобразование, центральная симметрия, осевая, параллельный перенос, поворот плоскости, скользящая симметрия.
Классификация движений:(существ-т 6 типов движений):
1-го рода: поворот на угол 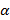 : 1)
: 1) 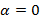 - тождественное преобразование. 2)
- тождественное преобразование. 2) 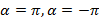 -центральная симметрия.3)
-центральная симметрия.3) 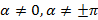 - новый поворот
- новый поворот 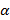 . 4) параллельный перенос.
. 4) параллельный перенос.
2-го рода: 5) осевая симметрия 6) скользящая симметрия
Пространство: Движение пл-ти в прост-ве ввод-ся аналог-но введения движения на пл-ти
Т. 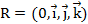
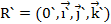
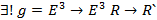
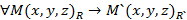
Т. 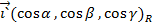 ,
, 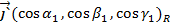 ,
, 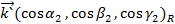
Типы(виды) движений :тождественное преобразование, парал-й перенос, центральная симм-я, сим-я отн-но пл-ти, поворот вокруг прямой, сим-я от-но прямой – поворот пространства на угол 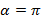 , поворот-е отраж-ие- композиция поворота и симметрии от-но пл-ти, скользящее отражение- это композиция симметрии от-но пл-ти и прал-го переноса на вектор р парал-ый плоскости, винтовое движение - композиция поворота вокруг прямой d и парал-го переноса на вектор р парал-ый d.
, поворот-е отраж-ие- композиция поворота и симметрии от-но пл-ти, скользящее отражение- это композиция симметрии от-но пл-ти и прал-го переноса на вектор р парал-ый плоскости, винтовое движение - композиция поворота вокруг прямой d и парал-го переноса на вектор р парал-ый d.
В основу классификации движений плоскости положено наличие инвариантных точек и инвариантных прямых.
Опр. Точка плоскости называется инвариантной (неподвижной), если при преобразовании оно переходит в себя.
Опр.Прямая называется инвариантной (неподвижной), если при преобразовании любая её точка переходит в точку этой же прямой.
Прямая, любая точка которой при преобразовании переходит в себя, называется прямой инвариантных точек. Прямая инвариантных точек является частным случаем инвариантных прямых.
Лемма Если движение g не имеет инвариантных точек, то это движение имеет, хотя бы, одну инвариантную прямую.
Доказательство:1. Пусть точка A – произвольная точка плоскости. A 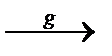 A1,A
A1,A 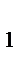
 A
A  .
.
2. По условию леммы точки A, A  , A
, A  различны (они не совпадают).
различны (они не совпадают).
 |
 |
| C1 |
| O1 |
| A1 |
| C |
| O2 |
| A |
| A2 |
 |
 |
 |
 |
 |
 |
 |
а) если А, A 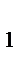 , A
, A 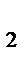
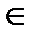 а , то очевидно, что а – инвариантная прямая.
а , то очевидно, что а – инвариантная прямая.
б) если А, A 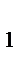 , A
, A 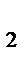
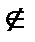 а.
а.
АО 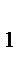 = O
= O 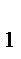 A
A 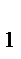 , А
, А 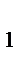 О
О 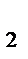 = O
= O 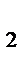 A
A 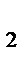 .
.
Докажем, что прямая O 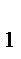 О
О 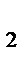 является инвариантной.
является инвариантной.
- Построим серединный перпендикуляр l 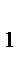 к отрезку АA
к отрезку АA 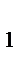 и серединный перпендикуляр l
и серединный перпендикуляр l 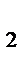 к отрезку A
к отрезку A 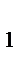 A
A 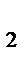 .
. 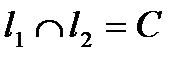 . Очевидно,
. Очевидно, 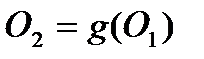 , поэтому
, поэтому 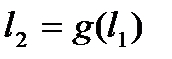 .
.
Так как 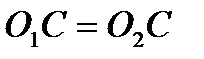 , то точка
, то точка 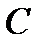 прямой
прямой 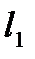 переходит либо в ту же точку
переходит либо в ту же точку 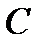 прямой
прямой 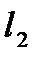 , либо в точку
, либо в точку 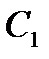 , симметричную точке
, симметричную точке 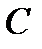 относительно точки
относительно точки 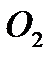 .
.
Первый случай не может иметь места, так как 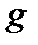 не имеет неподвижных точек, поэтому
не имеет неподвижных точек, поэтому 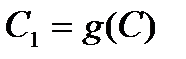 . Таким образом, прямая
. Таким образом, прямая 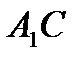 переходит в параллельную ей прямую
переходит в параллельную ей прямую 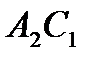 и четырехугольник
и четырехугольник 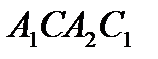 - параллелограмм.
- параллелограмм.
- Найдем образ прямой O 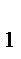 O
O 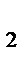 при этом движении.
при этом движении.
Пусть прямая m является образом прямой O 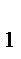 O
O 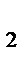 .
.
Так как О 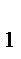 O
O 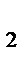
 A
A 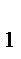 C , то образ прямой m перпендикулярен образу прямой A
C , то образ прямой m перпендикулярен образу прямой A 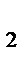 C
C 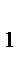 . Но A
. Но A 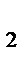 C
C 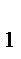
 O
O 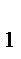 O
O 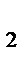 , то есть m совпадает с
, то есть m совпадает с 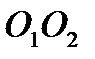 . Значит, значит
. Значит, значит 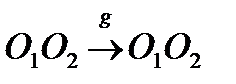 , т.е. O
, т.е. O 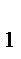 O
O 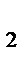 является инвариантной.
является инвариантной.
ЛеммаЕсли движениеg переводит луч h в себя, то это движение либо тождественное преобразование, либо отражение от некоторой прямой, содержащей луч h.
