Среднее арифметическое, гармоническое, геометрическое.

Рассмотрим два ряда распределения относительного признака – скорости и определим в каждом случае среднюю скорость.

V
T

Автомобиль ехал два участка со скоростями 50, 80 км/час в течение 1 и 4 часов соответственно.

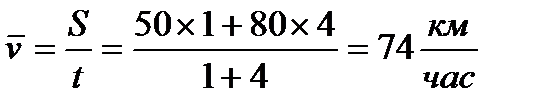
V
S

Автомобиль ехал со скоростями 50, 80 км/час два участка длиной 100 и 80 км соответственно.

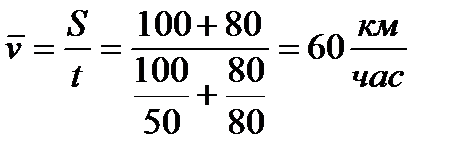
В общем случае формулы расчета называются формулами средних арифметического( множества чисел — сумма всех чисел, делённая на их количество. ) и гармонического (деление числа данный величины на сумму величинодратно данным ).

X	x1	x2	...	xn
F	f1	f2	...	fn

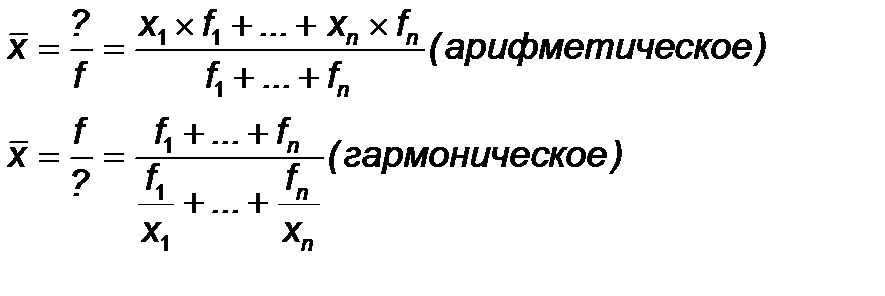
Выбор формулы зависит от связи двух признаков. Если она обратная, используется первая формула, прямая – то вторая. Например, по цене 100 руб./шт. было продано товара на 1000 руб., по 105 – на 2100, по 140 – на 2800. Определить среднюю цену.

Цена, руб./шт.
Сумма, руб.

Связь прямая: 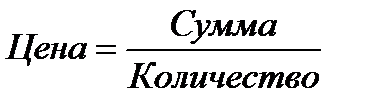, значит, используется формула среднего гармонического (=118).

Среднее геометрическое(двух чисел также называется их средним пропорциональным, поскольку среднее геометрическое двух чисел и обладает следующим свойством: , то есть среднее геометрическое относится к первому числу так же как второе число к среднему геометрическому.)

Рассмотрим относительную величину: рост признака = стало / было.

В первый раз значение признака увеличилось в 2 раза, во второй – в 18 раз. Во сколько раз в среднем происходит увеличение? Если воспользоваться формулой среднего арифметического, n = (18+2)/2 = 10. Но в таком случае за два раза прирост составил бы 10 ´ 10 = 100 раз, а по условию 2 ´ 18 = 36. Здесь решением будет 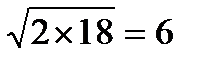, действительно, 6 ´ 6 = 36.

В общем случае, если признак последовательно увеличивался в x₁, x₂,...x_n раз, то средний прирост может быть получен по формуле среднего геометрического:

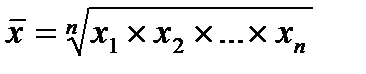
Статистическая зависимость. Коэффициент корреляции.

Две случайные величины связаны статистически, если распределение одной зависит от значения, которое принимает другая (для сравнения: связаны функционально, если значение одной зависит от значения другой; при функциональной зависимости любому значению одной величины жестко соответствует некоторое значение другой).

Частный случай статистической связи – корреляционная, при которой среднее значение одной случайной величины зависит от значения другой (на рис. – слева). Справа показаны статистически связанные величины, которые не коррелированны – среднее значение y для всех x постоянно; однако распределение все же изменяется – увеличивается дисперсия (разброс) y. Для получения представления о наличии статистической связи используют диаграмму рассеяния (на рис.): каждая точка соответствует паре значений (x, y) одной единицы совокупности, например, (рост, вес) одного человека.

y

●

●

●

○

●

●

●

●

○

○

●

●

●

●

○

○

○

●

●

●

●

●

○

○

○

○

○

●

○

○

○

○

○

○

●

●

●

○

○

○

○

○

●

○

○

X

Коэффициент корреляции

Для корреляционной связи двух величин существует оценка ее величины – коэффициент корреляции.

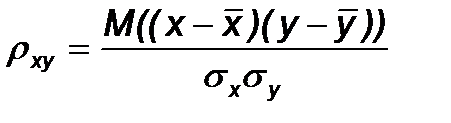
Свойства коэффициента корреляции:

1) для всех случаев значения находятся в интервале [–1,1];

2) для независимых величин равен нулю (обратное не обязательно верно!);

3) для связанных линейным соотношением y = kx + b он равен 1 или –1.

О силе связи судят по абсолютному значению коэффициента корреляции – чем оно больше, тем связь сильнее.

Элементы теории графов.

Оптимизация – поиск наилучшего по какому-либо критерию решения из возможных.

В качестве узла отмечают начало работы;

дуги – процесс ее выполнения. Узлов должно быть столько, сколько имеется работ; дуг – ровно столько, сколько чисел указано в колонке «работа». Дуги соединяют связанные работы: предварительная работа начинается, идет и только после ее окончания наступает зависимая работа. Числа на дугах соответствуют времени работ.

26. Задача определения пропускной способности сети.

Для сети, у которой известны пропускные способности дуг, определить пропускную способность всей сети – максималь­ный поток ресурса, который может поступать от источника к стоку.

Уже первое рассмотрение сети позволяет сделать вывод, что из узла (1) – источника не может вытекать поток более чем 8 + 2 = 10, а в узел (4) - сток не может втекать поток более чем 6 + 1 = 7, ведь потоку приходится проходить именно по дугам с такими пропуск­ными способностями. Понятно, что поток не будет превышать min (10,7) = 7.

разрез сети – любое множество дуг, исключение которых отделяет источник от стока и не дает ресурсу перемещаться от первого ко второму.

Задача решается на основе теоремы о максимальном потоке:

Максимальный поток = минимальному разрезу.

Среди всех разрезов ищется с минимальной суммой, эта сумма и определяет пропускную способность всей сети.

На рисунке примера минимальным разрезом будет {(1,2),(3,4)}. Сумма пропускных способ­ностей его 2+1=3 – самая маленькая, значит, и максимальный поток через данную сеть будет иметь значение 3.

27. Задача сетевого планирования.

Для комплекса работ, о каждой из которых известны время ее выполнения и перечень работ, которые должны быть завершены до ее начала, определить:

1). время начала каждой из работ;

2). время окончания всего комплекса.

Рассмотрим пример:

Работа	Время выполнения	Работы, которые должны быть выполнены предварительно
1.
2.
3.
4.		1, 2
5.		3, 4

g rr1u2Cg47D/fChAhImtsPZOCJwVYLkYvcyy1f3BF9100IkE4lKjAxtiVUobaksMw8R1x8k6+dxiT 7I3UPT4S3LXyPcty6bDhtGCxo5Wl+rK7OQVrszHb1ReZqi2OeXW6nq373iv1Oh4+ZiAiDfE//Nde awVFDr9f0g+Qix8AAAD//wMAUEsBAi0AFAAGAAgAAAAhANvh9svuAAAAhQEAABMAAAAAAAAAAAAA AAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAWvQsW78AAAAVAQAACwAA AAAAAAAAAAAAAAAfAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEArV4g4sMAAADbAAAADwAA AAAAAAAAAAAAAAAHAgAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAADAAMAtwAAAPcCAAAAAA== "> I 4trrho2C793iZQoiRGSNrWdScKUAZfH4MMNc+wtXdN5GIxKEQ44KbIxdLmWoLTkMI98RJ2/ve4cx yd5I3eMlwV0r37JsLB02nBYsdjS3VB+3v07B0qzMZv5FpmqnP+NqfzpYt94p9fw0fH6AiDTEe/i/ vdQK3ifw9yX9AFncAAAA//8DAFBLAQItABQABgAIAAAAIQDb4fbL7gAAAIUBAAATAAAAAAAAAAAA AAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhAFr0LFu/AAAAFQEAAAsA AAAAAAAAAAAAAAAAHwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAEfLE6TEAAAA2wAAAA8A AAAAAAAAAAAAAAAABwIAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAAAwADALcAAAD4AgAAAAA= "> Для решения имеющуюся информацию отображают на сетевом графике: в качес­тве узла отмечают нача­ло работы; дуги – процесс ее выполнения. Узлов должно быть столько, сколько имеется работ; дуг – ровно столько, сколько чисел указано в третьей колонке. Дуги соединяют связанные работы: предварительная работа начинается, идет и только после ее окончания наступает зависимая работа. Числа на дугах соответствуют времени работ.

Источниками на полученном графе будут работы, которые не ожидают выполнения каких-либо других работ и могут начаться с самого начала работ. Стоки соответствуют тем работам, которых не ждет ни одна из других работ, поэтому по завершении работы-стока может закончиться и весь комплекс работ.

Вводятся две фиктивные работы: «Начало» и «Конец» работ, и соединяются со всеми источниками и стоками соответственно. Фиктивные работы не требуют времени выполнения, их иногда называют событиями.

Алгоритм и его свойства.

Алгоритм – множество действий, связанных последовательностью выполнения. Может быть представлен в различной форме, главное, чтобы были отражены действия и связи следования. Например, может быть представлен в виде описания на языке (в том числе на алгоритмическом – специальном языке программирования). Иногда алгоритм представляется графически – в виде графа (блок-схемы). При этом узлы, описывающие действия, обозначаются с учетом специализации действий. Например, действие, заключающееся в проверке условия, обозначается ромбиком; в этом случае из него должны выходить две связи следования – в случае положительного и отрицательного результатов проверки. Обычное действие обозначается прямоугольником.

Свойства алгоритма: понятность для исполнителя, простота, правильность, число действий, число шагов (некоторые действия могут выполняться многократно), устойчивость (то есть насколько он работает правильно для различных данных), универсальность (насколько широко применим), скорость работы, точность (для приближенных алгоритмов), тип (по структуре – циклический, линейный,...).