Выборочные среднее, дисперсия.

Статистический ряд (выборка)

Значения x

x1

...

xn

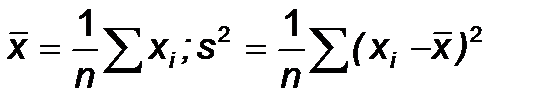
Ряд распределения (частотный)

Значения x	x1	...	xn
Частоты f	f1	...	fn

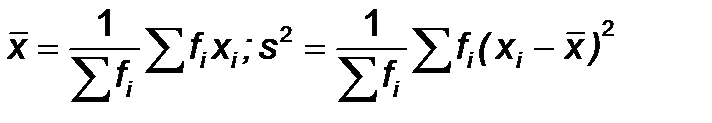
Интервальный ряд распределения

Интервалы x	x1 – x2	...	xn-1 – xn
Частоты f	f1	...	fn

При получении статистик интервалы заменяются на свои середины:

X₁ = (x₁ + x₂)/2, ...

Пример.

Срок расследования	до 1 мес.	1 – 2 мес.	2 – 3 мес.	3 – 4 мес.	4 - 6 мес.	6 - 12 мес.	12 - 18 мес.
Число уголовных дел

Средний срок расследования = 1/100 (0,5´ 10 + 1,5´ 40 + 2,5 ´ 25 + ...)

						Mx	s2
							2,8
							5,6
x
f
x
f
x
f

Выборочные мода, медиана.

Медиана определяется таким образом, чтобы в выборке меньше ее и больше было одинаковое число значений. Для ее получения строится вариационный ряд и изучается его среднее положение:

2 3 5 910 20 100 для нечетного числа значений Me = 9

2 2 4 5 610 20 100 для четного числа значений Me = (5 + 6) /2 = 5,5.

Мода для выборки – наиболее часто встречающееся в выборке значение.

Например, для выборки x = 2, 5, 5, 3, 2, 3, 2, 1 Mo = 2

Для ряда распределения:

X		5	6
F	8	4	4

Mo = 3, Me = 4

Для интервального ряда точка моды для интервала с наибольшей частотой определяется сложнее:

X	x1 – x2	x2 – x3	x3 – x4
F	f1	f2	f3

		f2
	f1
			f3
		Mo
	x1	x2	x3	x4

_--+--------

X	0 – 8	8 –16	16 –24
F	3	9	7

Mo = 8 + 8 / (1 + 2/6) = 14

X	0 – 5	5 –10	10 –15
F	2	5	3

x	5 – 10	10 –15	15 –20
f	5	20	10

Mo = 8

Mo = 13

Ошибка репрезентативности выборки.

ошибка репрезентативности – статистика, которая характеризует выборку по некоторому признаку и вычисляется:

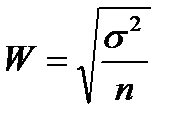
Например, в выборке 100 человек, 10 из них – девушки. Определить ошибку репрезентативности W для выборки (признак атрибутивный, может быть заменен на 0/1).

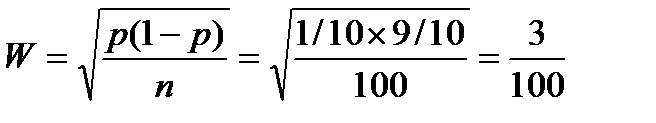
Определение необходимого объема выборки.

Существует и обратная задача – по определенному уровню допустимой ошибки репрезентативности определить n – минимально необходимый объем выборки:

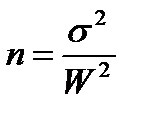
Необходимый объем выборки следует учесть величину ошибки выборочного исследования и доверительный уровень.

Абсолютные и относительные величины.

Абсолютные величины – не зависят от других, измеряются простыми единицами: стоимость – руб., расстояние – м, вес – кг, объем – м³ и т.д.

Относительные величины – представляются в виде отношения (частного) двух других. Единицы измерения часто имеют вид отношения, например, скорость - км/час, цена - руб./шт., руб./кг, производительность – шт./мин., расход топлива – л/км, плотность вещества – кг/м³, плотность населения – чел/км². Иногда величины оказываются безразмерными (в результате сокращения единиц), например, при вычислении доли от целого, темпов изменения во времени, отношения одной части целого к другой:

доля раскрытых преступлений = раскрытых (преступлений)/ общее количество (преступлений);

рост преступности = стало / было;

соотношение осужденных = мужчин / женщин.