Метод матрицы Джонса и матрицы Мюллера

В эллипсометрии для характеризации изменения состояния поляризации волны, прошедшей через слой или систему n слоев, Джонсом введена матрица M , которая носит его имя :

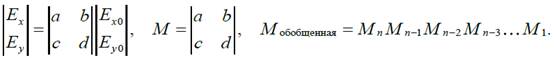
Матрица Джонсапригодна для описания полностью поляризованного света и ее вид определен для всех основных элементов эллипсометра: поляризатора, анализатора, компенсатора (четвертьволновой пластинки). Для образца матрица Джонса неизвестна и ее определение является смыслом обратной задачи эллипсометрии (ОЗЭ).

Полностью или частично поляризованный свет можно описать с помощью 4-вектора Стокса S, имеющего компоненты: S0, S1, S2, S3, и определяемого в Декартовых координатах для электромагнитной волны с

компонентам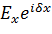и и 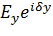, следующим образом:

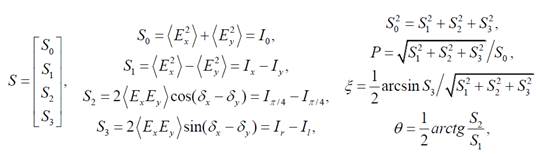
где I – интенсивности световой волны, P -степень поляризации, x и q -эллиптичность и азимут поляризованного света. Таким образом, используя параметры Стокса, изменение состояния поляризации в случае, как полностью, так и частично поляризованной падающей волны можно описать 4´4 матрицей Мюллера. Кроме того, с помощью 4´4 матрицы Мюллера можно определить степень деполяризации света. Если перейти к нормированному вектору Стокса s , то любой поляризующий элемент изменит состояние поляризации, которое описывается новым вектором Стокса s¢ , преобразованным умножением на матрицу Мюллера, состоящей из 16 элементов. Изменение вектора Стокса, обусловленное воздействием всех элементов системы, описывается обобщенной матрицей Мюллера:

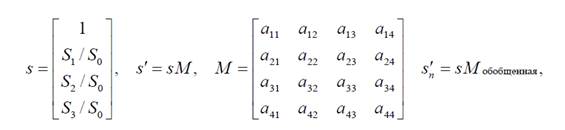
для отыскания aik элементов каждой матрицы необходимо решить 16 линейных уравнений, если известно воздействие каждого устройства оптической системы.

Метод четырехполюсника

(Амплитудная и фазовая передаточные функции (ATF и PhTF) отражающей системы)

Прибор для измерения состояния поляризации, называемый эллипсометром, схематично изображен на Рис. 1а, где исследуемая оптическая система, чей нормализованный вектор Джонса измерен, представлена «черным ящиком S» с передаточной функцией для комплексной амплитуды волны (CATF-Complex Transfer Function) при прохождении через оптическую систему. CATF можно разложить на две действительные: амплитудную и фазовую передаточные функции (ATF-Amplitude Transfer Function и PhTF-Phase Transfer Function). Схема сбора и обработки данных эллипсометра с фазовой модуляцией сигнала представлена на Рис. 1б. На вход поляризатора падает свет с круговой поляризацией (или циркулярно поляризованный), чтобы интенсивность прошедшего света не зависела от азимута собственной плоскости поляризатора. Интенсивность света на выходе эллипсометра зависит от азимутов элементов P, C, A и свойств исследуемой отражающей системы. В нуль-эллипсометрах задается комбинация азимутов Р и С, чтобы получить такую эллиптическую поляризацию света, которая дает линейно поляризованный свет при отражении от S, и тогда может быть найден ортогональный азимут гашения анализатора. Следовательно, интенсивность на выходе нуль-эллипсометра равна нулю (в идеальном случае) или близка к нулю (для большинства измеряемых отражающих систем). В ненулевых (фотометрических) эллипсометрических методах измерения интенсивность светового пучка на выходе эллипсометра определяется при нескольких комбинациях азимутов оптических элементов P, C, A

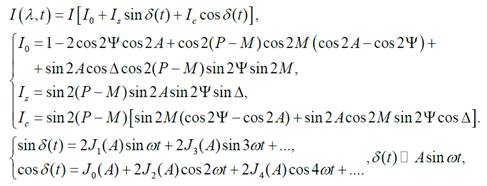
Уравнения (11а-11б) определяют амплитудную и фазовую передаточные функции (ATF и PhTF) измеряемой системы. Ненулевые методы широко используются при автоматизации измерений и мониторинге (с обратной связью) процессов изготовления стратифицированных структур для современных приборов и устройств.