Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
1. x2 + 9x = 0;
2. x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной xили свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
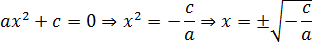
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
1. Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c/a) < 0, корней нет.
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
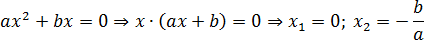
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
1. x2 − 7x = 0;
2. 5x2 + 30 = 0;
3. 4x2 − 9 = 0.
x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.
5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x2 − 9 = 0 ⇒ 4x2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Квадратные неравенства.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже..." )
Что такое "квадратное неравенство"? Не вопрос!) Если взять любое квадратное уравнение и заменить в нём знак "="(равно) на любой значок неравенства (> ≥ < ≤ ≠), получится квадратное неравенство. Например:
1. x2-8x+12≥0
2. -x2+3x>0
3. x2≤4
Ну, вы поняли...)
Я не зря здесь связал уравнения и неравенства. Дело в том, что первый шаг в решении любого квадратного неравенства - решить уравнение, из которого это неравенство сделано. По этой причине - неспособность решать квадратные уравнения автоматически приводит к полному провалу и в неравенствах. Намёк понятен?) Если что, посмотрите, как решать любые квадратные уравнения. Там всё подробно расписано. А в этом уроке мы займёмся именно неравенствами.
Готовое для решения неравенство имеет вид: слева - квадратный трёхчленax2+bx+c, справа - ноль. Знак неравенства может быть абсолютно любой. Первые два примера здесь уже готовы к решению. Третий пример надо ещё подготовить.
Подготовка заключается в тождественных преобразованиях неравенств. Прогуляйтесь по ссылке, если хотите узнать главную ошибку учеников при решении любых неравенств.) Там всё просто. Да и полезная информация по неравенствам имеется.
Решение квадратных неравенств. Примеры.
Квадратные неравенства можно решать двумя способами. Один способ - это метод интервалов. Великий и могучий! Годится для любых неравенств вообще! Ему будет посвящён отдельный урок. Здесь же мы разберём более простой способ с использованием парабол. Зачем из пушки по воробьям палить?) Способ годится только для решения квадратных неравенств. Но прост, очень нагляден и не требует никаких особых расчётов. Что, между прочим, резко уменьшает количество ошибок...
Решение будем разбирать на конкретных примерах. Сразу обрадую: любые квадратные неравенства решаются так, как написано далее. Любое решение состоит из трёх шагов. Первый пример я распишу очень подробно. Для понимания. Кто осилит решение до конца, получит приятный бонус.)
Ну что, начнём?)
1. Решить неравенство:
x2-8x+12≥0
Это неравенство уже готово для решения. Слева - квадратный трёхчлен, справа - ноль. Можно приступать.
Первый шаг решения.
Первый шаг всегда одинаков и прост до ужаса.) Делаем из неравенства уравнение:
x2-8x+12 = 0
Решаем это уравнение.
Знак неравенства на этом этапе нас совершенно не интересует.
Решаем, как обычно, без всяких фокусов, через дискриминант. Получаем корни:
х1= 2
х2= 6
Первый шаг сделан. Можно передохнуть.) Сейчас начнётся самое интересное.
Второй шаг решения.
На этом шаге мы ничего решать не будем. Мы будем рисовать.) Да-да! Квадратные неравенства, как правило, решаются графически.
Знак неравенства и на этом этапе нас совершенно не интересует.
Слово "парабола" вам знакомо?) Вам повезло. В этом случае специально запоминать ничего не придётся. Один раз разобраться, и проблем не будет. В противном случае придётся запомнить алгоритм решения механически... Алгоритм приведён ниже.
Итак, на первом шаге мы из неравенство сделали уравнение. Решили его. На втором шаге из уравнения сделаем параболу:
y = x2-8x+12
Нарисуем эту параболу на графике. Вот такая она получится:
Точки 2 и 6 - это корни уравнения x2-8x+12 = 0, если помните...) Они располагаются прямо на оси ОХ. Почему так? А как же!? Сравните уравнение и параболу:
x2-8x+12 = 0
y = x2-8x+12
Корни уравнения - это иксы, при которых в правой части уравнения получается ноль. Стало быть, при таких иксах, и игрек нулевой будет. Выражения-то одинаковые. А нулевой игрек - это, как раз, ось ОХ и есть.
Фиксируем в голове: корни уравнения (2 и 6) - это значения икса, при которых выражение x2-8x+12 равно нулю. Это важно!
А теперь прикинем: при каких иксах выражение x2-8x+12 будет больше нуля? Как раз для такой прикидки нам и нужна парабола. Выражение x2-8x+12 это же и есть наш игрек. На графике чётко видно, где игрек больше нуля (положительный) и где он меньше нуля (отрицательный). Наводим мышку на рисунок (или касаемся картинки на планшете) и всё видим.
Если возьмём любую точку левее х=2, например х2, то соответствующий ему у2 будет положительный. Если возьмём точку х1 ещё левее, то пунктир пересечёт график далеко вверху, за пределами картинки, но игрек будет всё равно положительный.
Если мы возьмём икс правее точки х=6, скажем, х5, снова получим положительныйу5.
Если же мы возьмём любую точку между х=2 и х=6, например х3 или х4 - мы получим соответствующие им отрицательные значения у3 и у4.
Улавливаете идею?)
По параболе сразу видно, при каких иксах наш игрек (а это выражение x2-8x+12, между прочим!) больше нуля, меньше нуля и равен нулю!
По параболе, визуально, мы мгновенно определили знаки выражения x2-8x+12 при различных иксах. Можно нарисовать вот такую картину:

При всех иксах, которые меньше (левее) двойки, парабола проходит выше оси ОХ. Игрек при таких иксах - положительный, т.е. больше нуля. Следовательно, наше выражение x2-8x+12 при таких иксах больше нуля. Если мы убежим влево за рисунок, возьмём икс, равный минус сто миллионов, всё равно наше выражение будет больше нуля. Много-много больше.) Парабола - она бесконечная, и внезапно загибаться вниз не может.)
Аналогичная картина получится, если мы возьмём любой икс, больше (правее) шестёрки. Эти области на графике отмечены знаком "плюс"
А вот если мы возьмём любой икс в промежутке между 2 и 6, получим игрек отрицательный. Следовательно, при таких иксах, наше выражение меньше нуля.
Вот, практически и всё. На этом шаге мы руками нарисовали график, глазами увидели параболу, головой сообразили где какие знаки.) Осталось всего ничего.
Третий шаг решения.
На последнем шаге нужно вспомнить, что нам НЕ сказано было "решать уравнение"... НЕ сказано было "строить график"... Это, всего лишь, наши подручные средства.
Нам было сказано: решать квадратное неравенство!
Знак неравенства на этом этапе играет главную роль!
Смотрим на исходное неравенство:
x2-8x+12≥0
Нам нужно найти все иксы, при которых выражение в левой части неравенство больше, либо равно нулю. А чего их искать? Мы уже всё нашли.) Смотрим на график и видим, что это условие выполняется в областях, где стоит знак "+", (игрек больше нуля) и в точках х=2 и х=6 (игрек равен нулю).
