Последовательное соединение активного, индуктивного и ёмкостного сопротивлений

При последовательном соединении каждый участок цепи имеет свою величину напряжения.

.

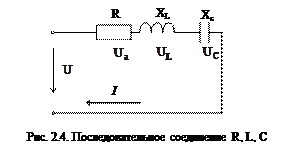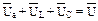Это выражение представляет собой запись второго закона Кирхгофа в векторной форме.

При построении диаграммы условно принято, что 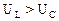. Вектор напряжения на активном сопротивлении 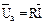совпадает по направлению с вектором тока, его называют активной составляющей напряжения.

Вектор напряжения на индуктивном сопротивлении 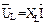опережает вектор тока I на угол 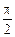(направлен вверх). Вектор напряжения на емкостном сопротивлении 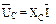отстает от вектора тока I на угол 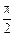(направлен вниз). Замыкающий вектор изображает приложенное к цепи напряжение U, сдвинутое по фазе относительно тока на угол φ (рис. 2.5).

Выделим из векторной диаграммы треугольник ОАВ (рис. 7). Этот треугольник называется треугольником напряжений.

Сторона АВ называется реактивной составляющей напряжения:

.

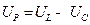Из треугольника напряжений получается простое соотношение:

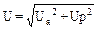или .

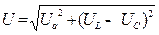Если все стороны треугольника напряжений ОАВ разделить на величину тока, получим треугольник сопротивлений (рис. 2.7).

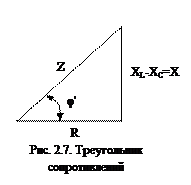Гипотенуза этого треугольника соответствует полному сопротивлению Z.

Разность индуктивного и емкостного сопротивлений называется реактивным сопротивлением:

.

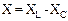Из треугольника сопротивлений получаются важные расчетные соотношения:

,

, .

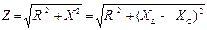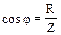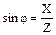Закон Ома для цепи имеет вид: .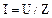

Параллельное соединение. Активная, реактивная и полная проводимости

При построении векторной диаграммы ток I ветви разложим на составляющие:

- активную составляющую I_a , совпадающую с напряжением U по фазе;

- индуктивную составляющую I_L, отстающую по фазе от напряжения U на угол ;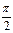

- емкостную составляющую I_c, опережающую напряжение по фазе на угол .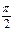

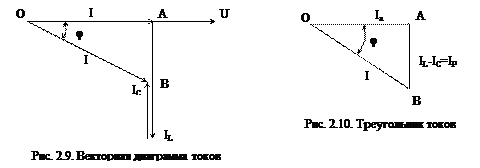Выделим из векторной диаграммы треугольник ОАВ. Этот треугольник называется треугольником токов (рис. 2.10). Сторона АВ называется реактивной составляющей токов:

.

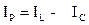Из треугольника токов получается соотношение между током I цепи и его составляющими:

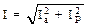или .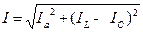

Разделим все стороны треугольника токов на напряжение U , получим треугольник проводимостей (рис. 2.11). В этом треугольнике

g = I_a / U - активная проводимость, b_L = I_L / U - индуктивная проводимость,

b_C = I_C / U - емкостная проводимость, y = I / U - полная проводимость. Разность индуктивной и емкостной проводимостей называется реактивной проводимостью:

.

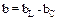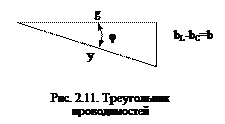Из треугольника проводимостей получаются следующие расчетные выражения:

,

, ,

,

, .

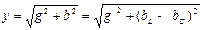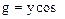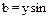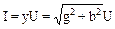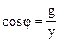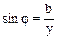Из сопоставления выражений для тока следует, что полная проводимость y равна обратной величине полного сопротивления:

.

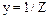Подставляя в выражения для активной и реактивной проводимостей значения y, sinφ, cosφ получим формулы преобразования последовательного соединения в параллельное:

,

.
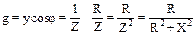
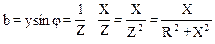