Стандартные распределение случайных величин, их свойства, характеристики и области применения

Стандартные распределение случайных величин, их свойства, характеристики и области применения

Экспоненциальное (показательное) распределение

Показательное распределение играет исключительную роль в теории надежности и в практике расчетов. Отметим сейчас, что во многих случаях промежуток времени между двумя последовательными отказами сложной системы подчиняется как раз показательному распределению.

Широкое использование данного закона в теории надежности объясняется тем, что экспоненциальный закон, физически очень естественный, прост и удобен для использования. Почти все задачи, возникающие в теории надежности для экспоненциальных законов распределения, оказываются на порядок проще, чем для произвольных законов. Почти все формулы в теории надежности в случае экспоненциального закона резко упрощаются.

Экспоненциальным законом распределения можно аппроксимировать время безотказной работы большого числа элементов. В первую очередь это относится к элементам радиоэлектронной аппаратуры, а также к машинам, эксплуатируемым в период после окончания приработки и до существенного проявления постепенных отказов. Экспоненциальное распределение применяется в областях, связанных с «временем жизни»: в медицине продолжительность жизни больных, в надежности – продолжительность безотказной работы устройства, в психологии – время, затраченное на выполнение тестовых задач. Оно используется в задачах массового обслуживания, в которых речь идет об интервалах времени между телефонными звонками, или между моментами поступления техники в ремонтную мастерскую, или между моментами обращения клиентов.

Экспоненциальное распределение выделяется среди других распределений свойством «отсутствия памяти». Пусть - время службы некоторого изделия с экспоненциальным законом распределения. «Отсутствие памяти» означает, что изделие, проработавшее время , имеет такое же распределение, что и новое, только что начавшее работу. Математически это свойство выражается в виде следующего неравенства:

Для любых . Данное свойство как бы исключает износ и старение изделия.

Плотность вероятности:

Параметр распределения:

.

Функция распределения:

Вероятность безотказной работы:

Интенсивность отказов:

.

Соотношения между моментами и параметром распределения :

Среднее время наработки до отказа:

.

Дисперсия и среднеквадратичное отклонение:

;

.

Коэффициенты асимметрии и эксцесса:

где

.

Медиана:

.

Коэффициент вариации:

.

Гамма-распределение

Гамма-распределение довольно часто встречается в приложениях теории вероятностей, особенно в математической статистике.

Этим типом распределения удобно приближать те законы надежности, у которых плотность распределения отказов имеет одновершинный несимметричный вид.

Плотность вероятности наработки до отказа:

— параметр масштаба , — параметр формы , — гамма-функция или эйлеров интеграл второго рода или

.

Аналитического выражения для функции распределения наработки на отказ не существует (аналитическое выражения для нее существует только для целых положительных значений параметра ; см. ниже распределение Эрланга).

Известны формулы связи моментов с параметрами и гамма-распределения:

; ; ; ; .

Коэффициент вариации:

.

Мода:

для значений . Квантиль находится из уравнения для

Точка перегиба:

Начальные моменты:

Параметр , характеризующий асимметрию гамма-распределения, определяет вид характеристик надежности. При интенсивность отказа возрастает, при убывает, а при становится постоянной, т.е. гамма-распределение превращается в экспоненциальное.

Распределение Эрланга

Плотность распределения наработки до отказа:

для ; ; — целое.

Функция распределения времени наработки до отказа:

Вероятность безотказной работы:

.

Интенсивность отказов системы в целом:

Соотношения между моментами и параметрами распределения определяются, как и у гамма-распределения, но с заменой параметра на .

Распределение Эрланга порядка k описывает распределение случайной величины как суммы k штук независимых случайных величин, каждая из которых распределена по показательному (экспоненциальному) закону с параметром .

Распределению Эрланга удовлетворяет время наработки до отказа резервированной системы с включением «холодного» резерва по способу замещения при условии, что наработка до отказа включенного элемента подчинена экспоненциальному закону. При этом , где m — число резервных элементов. Из соотношения вытекает свойство структур с «холодным» резервом – средняя наработка системы до отказа линейно возрастает от числа резервных элементов.

Распределение Релея

Распределение Релея вытекает из распределения Вейбулла-Гнеденко при .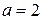

Плотность вероятности наработки до отказа:

,

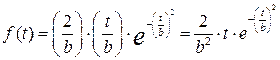
где ; .

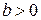Введя переобозначения 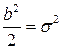, плотность вероятности можно представить в виде

.

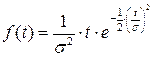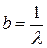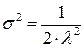Если принять , то , и 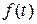принимает вид .

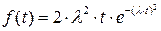Функция распределения времени наработки до отказа:

.

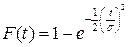Вероятность безотказной работы:

.

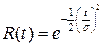Интенсивность отказов:

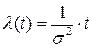
Соотношения между моментами и параметрами распределения:

Среднее время наработки до отказа T:

.

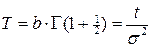Дисперсия D:

.

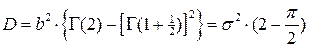Коэффициент асимметрии Sk:

.

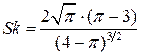Коэффициент островершинности Ex:

.

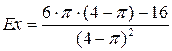Коэффициент вариации ν:

.

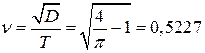Мода:

.

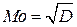Медиана:

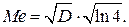
Нормальное распределение

Нормальный закон – наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Плотность вероятности наработки до отказа:

,

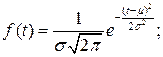
где ;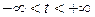

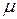- параметр положения (математическое ожидание);

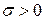- параметр масштаба (стандартное отклонение);

Функция распределения времени наработки до отказа:

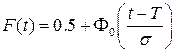, где 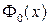- функция Лапласа.

Соотношения между моментами и параметрами распределения:

Среднее время наработки до отказа T:

;

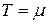Дисперсия D:

;

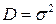Коэффициент асимметрии Sk:

;

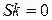Коэффициент островершинности Ex:

;

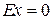Мода:

;

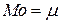Медиана:

;

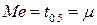Начальные моменты:

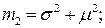
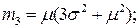
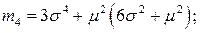
Центральные моменты:

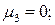
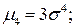
Точки перегиба функции плотности распределения :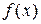

;

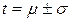Согласно закону больших чисел, распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие примерно равнозначные факторы. Нормальному распределению подчиняются ошибки измерения деталей, дальность полета снарядов и т.п. При большом времени работы элемента и наличии восстановления среднее число отказов имеет асимптотически нормальное распределение.

Стандартные распределение случайных величин, их свойства, характеристики и области применения