Моменты инерции относительно параллельных осей.

При рассмотрении нескольких осей, параллельных друг другу (рис.4), оказывается, что можно легко вычислить моменты инерции фигуры относительно любой из этих осей, зная ее момент инерции относительно оси, проходящей через центр тяжести фигуры параллельно выбранным осям.

Рис.4.

Рассмотрим произвольную фигуру. Проведем центральную ось Оу, момент инерции относительно этой оси назовем . Проведем в плоскости фигуры ось параллельно оси у на расстоянии от нее. Найдем зависимость между и — моментом инерции относительно оси . Для этого напишем выражения для и . Разобьем площадь фигуры на площадки dA; расстояния каждой такой площадки до осей у и назовем и . Тогда из рис.4 имеем:

Первый из этих трех интегралов — момент инерции относительно оси Оу. 2-ой — статический момент относительно той же оси; 3-й интеграл – площадь.

Так как ось Оу – центральная, то второе слагаемое— статический момент относительно той же оси равен нулю, так как ось у проходит через центр тяжести фигуры.

Таким образом,

,

т. е. осевой момент инерции относительно любой оси равен моменту инерции относительно центральной оси, проведенной параллельно у данной, плюс произведение площади фигуры на квадрат расстояния между осями; а центробежный момент инерции относительно системы взаимно перпендикулярных осей, параллельных центральным, равен центробежному моменту инерции относительно этих центральных осей плюс произведение из площади фигуры, на координаты ее центра тяжести относительно новых осей.

Зависимость между моментами инерции при повороте осей.

Центральных осей можно провести сколько угодно. Является вопрос, нельзя ли выразить момент инерции относительно любой центральной оси в зависимости от момента инерции относительно одной или двух определенных осей. Для этого посмотрим, как будут меняться моменты инерции относительно двух взаимно перпендикулярных осей при повороте их на угол .

Возьмем какую-либо фигуру и проведем через ее центр тяжести О две взаимно перпендикулярные оси Оу и Oz (рис.2).

Рис.2. Расчетная модель для определения моментов инерции для повернутых осей.

Пусть нам известны осевые моменты инерции относительно этих осей , , а также центробежный момент инерции .Начертим вторую систему координатных осей и наклоненных к первым под углом ; положительное направление этого угла будем считать при повороте осей вокруг точки О против часовой стрелки. Начало координат О сохраняем. Выразим моменты относительно второй системы координатных осей и , через известные моменты инерции и .

Напишем выражения для моментов инерции относительно этих осей.

Из чертежа видно, что координаты площадки dA в системе повернутых осей будут:

Подставляя эти значения и в (1), получим:

Также

Моменты инерции при повороте осей изменяются, и при некотором угле α экстремальные значения достигают максимума.

Оси, относительно которых осевые моменты инерции принимают экстремальные значения, называются главными осями инерции.

Относительно главных осей центробежный момент равен нулю. Оси, проходящие через центры тяжести, называются главными центральными осями.

Положение главных осей:

Значения главных центральных моментов инерции:

Лекция 4. Сдвиг (срез).

Понятие чистого сдвига. Элементы конструкций, работающих в условиях чистого сдвига. Деформации, напряжения. Площадки чистого сдвига. Закон Гука при сдвиге. Условие прочности при сдвиге (срезе).

Сдвиг (срез) - вид деформации, при котором одна часть стержня смещается относительно другой (скользит). Сдвиг, как вид нагружения, встречается редко и имеет место в заклепочных и сварных соединениях. Деформация сдвига происходит в случае, если к стержню приложены две равные по модулю противоположно направленные силы P , перпендикулярные к его продольной оси. Расстояние между этими силами должно быть малым, чтобы можно было пренебречь моментом, создаваемым силами.

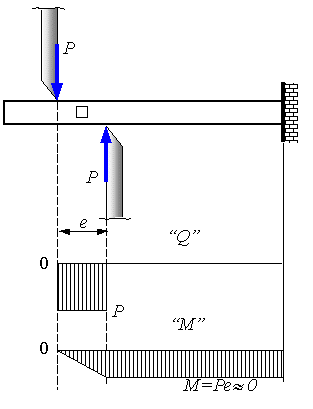
Используя метод сечений (разрезая стержень между силами P), можно установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная сила Q.

Такой вид нагружения, при котором в поперечных сечениях стержня действует только поперечная сила, называют чистым сдвигом.

Мера скольжения одного поперечного сечения относительно другого - касательные напряжения τ.

Принято, что касательные напряжения распределены по всей площади поперечного сечения равномерно.

Рис.1

Если в поперечном сечении стержня площадью A возникает внутренняя поперечная сила Q=P , то касательные напряжения в любой точке этого сечения будут равны: Τ = Q / A = P / A.

При чистом сдвиге возникает плоское напряженное состояние, тогда напряжения, действующие на площадке составляющей угол 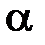с вертикальной исходной площадкой равны:

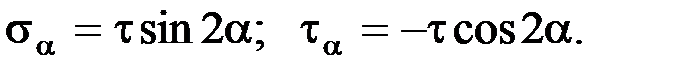
Касательные напряжения τ, приведенные на рис. 1, по абсолютной величине больше касательных напряжений по любым другим площадкам. Таким образом, они являются экстремальными, а площадки, по которым они действуют – площадками сдвига. Так как по этим площадкам не действуют нормальные напряжения, то их называют площадками чистого сдвига и они образуют с главными площадками углы, равные 45⁰.

При чистом сдвиге нормальные напряжения на любых двух взаимно перпендикулярных площадках равны друг другу по модулю и противоположны по направлению.

В результате сдвига одно поперечное сечение стержня смещается относительно другого на величину δ , называемую абсолютным сдвигом.

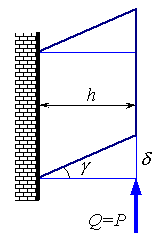
Малый угол γ, на который изменится первоначально прямой угол, – относительный сдвиг, выражается в радианах.

Угол сдвига 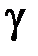пропорционален касательным напряжениям. Математическая зависимость между углом сдвига и касательным напряжением называется законом Гука при сдвиге:

.

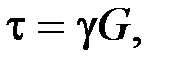Зависимость между модулем сдвига и модулем Юнга:

.

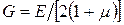Значение коэффициента Пуассона μ находится в пределах 0 ≤ μ ≤ 0,5.

Условие прочности при сдвиге имеет вид:

τ = Q / A ≤ [ τ ]

Кручение.

Крутящие моменты (внутренний силовой фактор) в поперечных сечениях стержня. Кручение стержней круглого поперечного сечения: допущения, деформации, напряжения, углы закручивания. Условия прочности, жёсткости. Построение эпюр крутящих моментов.

Кручение имеет место в случае действия на вал момента (пары сил) относительно его продольной оси, и в поперечных сечениях бруса возникает только один силовой фактор – крутящий момент. Брус, работающий на кручение называется валом. При кручении вала его поперечные сечения поворачиваются друг относительно друга, вращаясь вокруг оси бруса.

Напряжения и деформации при кручении бруса. Под действием внешнего скручивающего момента, приложенного на правом конце бруса, левый конец которого жестко закреплен, брус будет закручиваться. Выделим из бруса элементарный цилиндр длиной 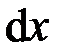. Будем считать, что левое сечение бруса жестко закреплено. Под действием крутящего момента 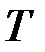правое сечение повернется на некоторый угол .

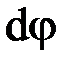Так как 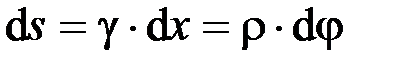, то получаем .

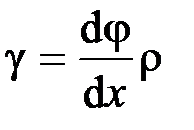Из данной зависимости видно, что угол сдвига 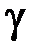изменяется по радиусу вала по линейному закону.

Деформация бруса при кручении характеризуется относительным углом закручивания .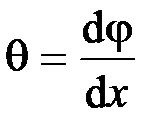

При малых углах закручивания вала в теории кручения круглых стержней принимаются допущения:

1. Поперечные сечения, плоские и перпендикулярные к его оси до деформации, остаются плоскими (не коробятся) и перпендикулярными к оси вала и после деформации (гипотеза Бернулли);

2. Радиусы поперечных сечений при деформации не искривляются и не изменяют своей длины;

3. Длина вала в результате закручивания не изменяется.

Поперечное сечение вала ведет себя при кручении, как жесткий диск, идеформациюкручения можно рассматривать, как результатсдвига одного поперечного сечения относительно другого. В этом случае в точках поперечного сечения вала возникают только касательные напряжения.

Теория кручения, основанная на упомянутых допущениях, подтверждается экспериментальными данными.

Согласно закону Гука при сдвиге, имеем 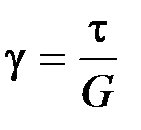. Откуда получаем: .

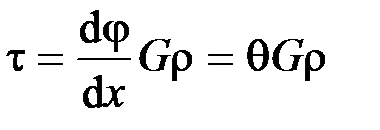Из полученной зависимости следует, что касательные напряжения изменяются по радиусу по линейному закону.

При кручении все внутренние силы, распределенные по поперечному сечению, приводятся к одной составляющей - к крутящему моменту. Крутящий момент 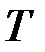в сечении бруса определяется по формуле

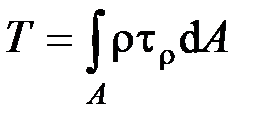, где 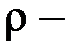плечо элементарной силы.

Подставляя значение касательного ускорения, получим

.

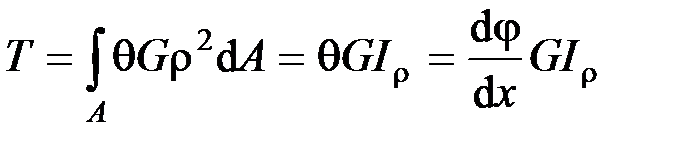Элементарный угол закручивания бруса: 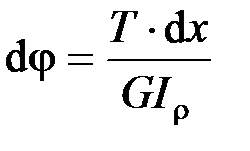; полный угол закручивания .

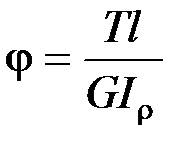Максимальное касательное напряжение в поперечном сечении бруса будет определяться по зависимости:

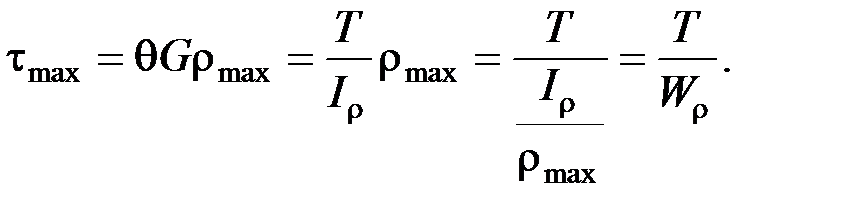
Прочность и жесткость при кручении. Условие прочности при кручении имеет вид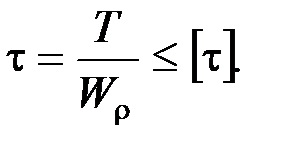

Условие жесткости: .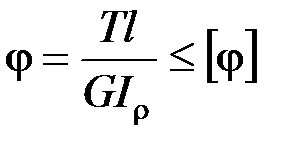

Для бруса круглого сечения эти условия принимают вид:

.

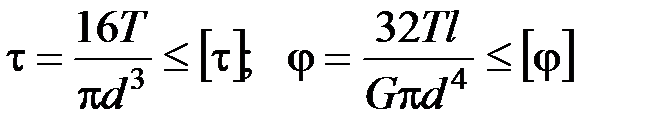Построение эпюр крутящих моментов.Крутящий момент равен алгебраической сумме скручивающих моментов, приложенных к любой из частей стержня. Эпюра крутящих моментов – это график, показывающий изменения крутящего момента по длине вала.

При построении эпюры крутящих моментов используется правило знаков: скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки при взгляде на поперечное сечение, вызывает в этом сечении положительный крутящий момент.

Брус разбивается на участке, на каждом участке проводится сечение и определяется крутящий момент. Затем строится эпюра крутящих моментов.

Лекция 5. Изгиб.

Плоский поперечный изгиб прямых стержней (брусьев, балок). Определение внутренних сил (поперечных сил и изгибающих моментов) в произвольном поперечном сечении стержня и построение их эпюр. Дифференциальные зависимости между нагрузкой, поперечными силами, изгибающими моментами, их использование при построении диаграмм и контроля правильности построения.

Под плоским поперечным изгибом понимают такой вид деформации, при которой происходит искривление оси прямого бруса, и в поперечном сечении бруса действует два силовых фактора: изгибающий момент М и поперечная сила Q. Осью бруса называется геометрическое место точек центров тяжестей поперечных сечений бруса. Изгиб - плоский, если ось балки после деформации остается плоской линией. В противном случае имеет место косой изгиб. Если поперечная сила не возникает, изгиб называется чистым изгибом.

Рассмотрим, например, балку, нагруженную вертикальной сосредоточенной силой P.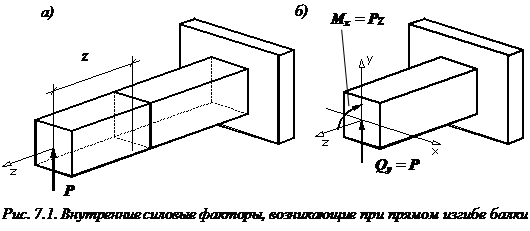

Разрежем мысленно балку в интересующем месте на две части. Отбросим левую часть балки, нагруженную силой P. Заменим действие отброшенной левой части балки на оставленную правую часть внутренними силами.

Внутренние усилия возникают во всех точках поперечного сечения балки и распределены по неизвестному закону. Не имея возможности определить эти внутренние усилия для каждой точки сечения, заменяем их статически эквивалентнымивнутренними силовыми факторами, приложенными в центре тяжести поперечного сечения.

Внутренние силовые факторы определяются из условия равновесия рассматриваемой части балки. Однако можем внутренние силовые факторы найти и непосредственно, как действие отброшенной левой части на правую часть. Видно, что часть балки, нагруженная силой P, стремится изогнуть рассматриваемую нами правую часть выпуклостью вниз, а также пытается произвести срез. Следовательно, в сечении должны возникнуть поперечная сила и изгибающий момент.

Осуществим параллельный перенос силы P в центр тяжести поперечного сечения балки. По правилам теоретической механики добавляется момент, равный .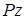

Таким образом, в поперечном сечении балки возникают два внутренних силовых фактора:

изгибающий момент, численно равный алгебраической сумме моментов всех сил, приложенных к отбрасываемой части балки, относительно главной центральной оси, проходящей через центр тяжести рассматриваемого сечения (в данном примере М= Рz);

поперечная сила, численно равная алгебраической сумме всех внешних сил (активных и реактивных), действующих на отбрасываемую часть балки, в нашем примере Q = P).

Построение эпюр поперечных сил и изгибающих моментов. При расчете балок на прочность необходимо знать характер изменения изгибающего момента и поперечной силы вдоль оси балки и знать положение опасного сечения. С этой целью строят эпюры поперечных сил и изгибающих моментов.

Если внешняя сила стремится повернуть отсеченную часть по часовой стрелке относительно рассматриваемого сечения, то поперечная сила положительна.

+Qy

+Mx

Изгибающий момент будет положительным, если при действии момента внешних сил балка искривляется выпуклостью вниз.

Построение эпюр поперечных сил и изгибающих моментов рассмотрим на конкретном примере.

Пусть на балку действует внешний изгибающий момент 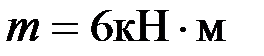и внешняя сила 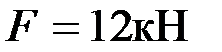, 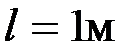. Определим реакции в опорах 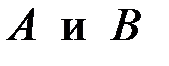. Составим уравнения равновесия моментов всех внешних сил относительно опор

;

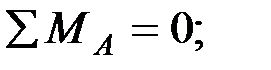
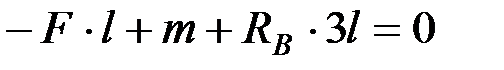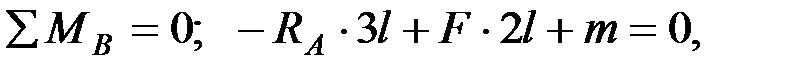
откуда

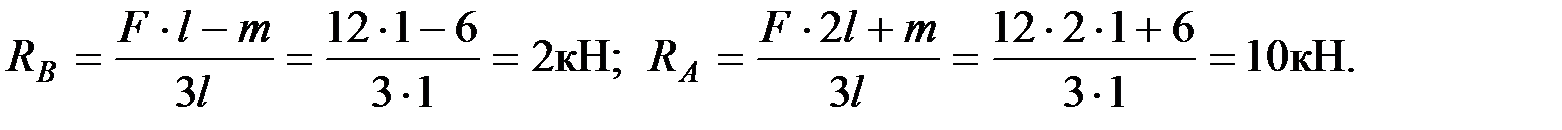
Проведем сечения на каждом характерном участке и определим значения поперечной силы 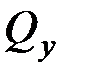и изгибающего момента .

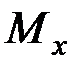В сечении 1

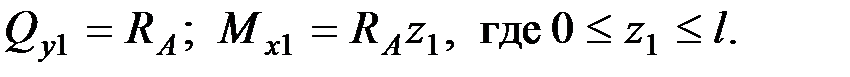
При ;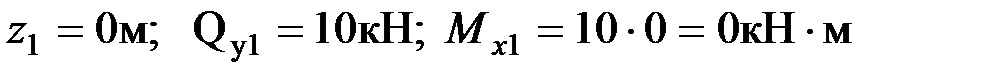

при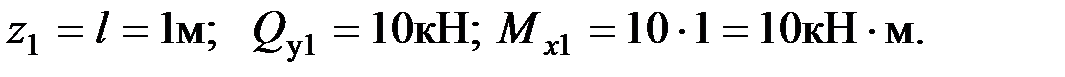

В сечении 2

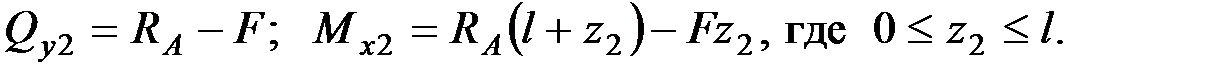
При ;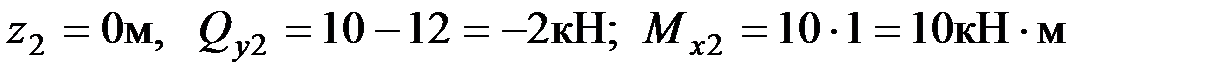

при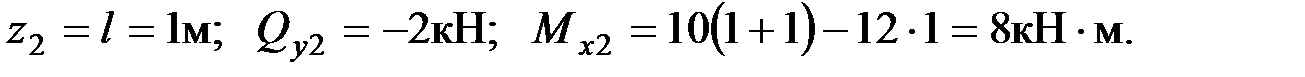

В сечении 3

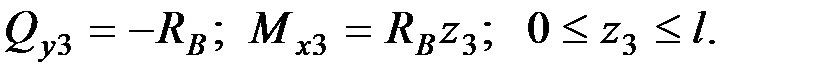
При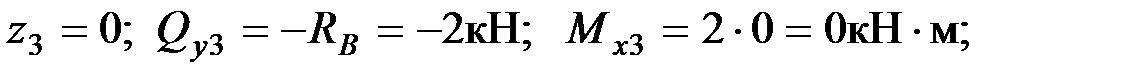

при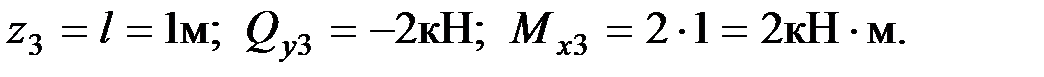

По полученным значениям строим эпюры поперечных сил и изгибающих моментов .