Моменты инерции относительно полюса и относительно плоскости

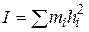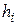Эти моменты инерции определяются аналогично осевым моментам формулой , где - расстояние от 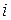- ой точки до полюса или до плоскости.

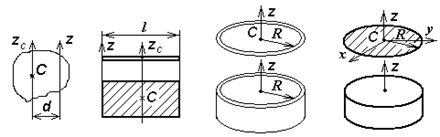
а б в г

Рис. 9. К расчету осевых моментов инерции

Полярный момент инерции относительно начала 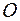декартовой системы координат

.

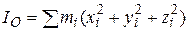Моменты инерции относительно координатных плоскостей

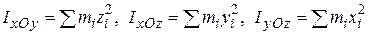Очевидны соотношения

.

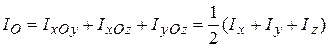Моменты инерции некоторых однородных тел

а) Стержень (прямоугольная пластина) постоянной толщины массой 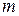и длиной 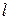(рис. 9,б)

; .

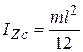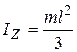б) Тонкий обруч (тонкостенная труба) радиуса 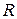(рис. 9,в)

.

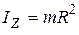в) Сплошной диск (цилиндр) радиуса 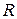(рис. 9,г)

.

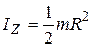Используя формулы п.3.2.8, найдем моменты 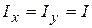для сплошного диска (рис. 9, г). Считаем толщину диска малой: 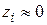, тогда

.

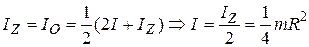В некоторых задачах (например, в статических задачах по сопротивлению материалов) требуется рассчитать момент инерции некоторой фигуры (сечения), плотность которой 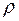условно считается равной единице. Тогда, например, последний момент будет равен 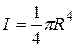(масса диска будет равна ).

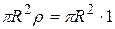Потенциальное силовое поле

Силовое поле – часть пространства (или все пространство), в каждом пункте которого определена, тем или иным физическим законом, сила, действующая на материальную точку, находящуюся в этом пункте.

Силовое поле называется потенциальным (имеющим скалярный потенциал), если существует дважды непрерывно дифференцируемая силовая функция 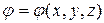, такая, что в каждой точке поля 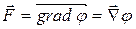, где символический вектор-оператор «набла» имеет следующий смысл:

.

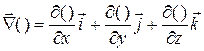Тогда работа силы 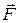при перемещении точки приложения силы из пункта 1 в пункт 2 равна (см. ч. 1, п. 2.1.7)

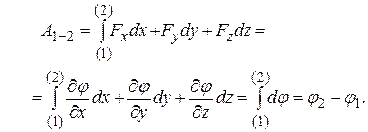
Работа определяется только начальным и конечным значениями силовой функции и не зависит от формы траектории. Работа на замкнутой траектории (контуре) равна нулю. Выражение для работы вектора силы 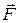определяет циркуляцию этого вектора вдоль траектории точки приложения силы. В потенциальном поле циркуляция силы 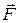вдоль любого замкнутого контура равна нулю:

.

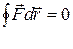Согласно формуле Стокса циркуляция вектора 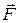вдоль замкнутого контура, стягивающего поверхность малой величины (так что ее можно считать плоской), равна интегралу по площади от проекции ротора вектора 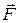на нормаль 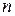к этой поверхности (ориентированную соответственно направлению обхода контура):

.

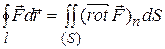Потенциальное силовое поле, задаваемое скалярным потенциалом 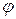, называется также безвихревым, поскольку в нем выполняется условие 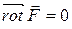(равенство 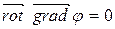- известное в теории поля тождество).

Ротор (вихрь, он же 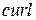) вектора 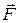определяется формулой

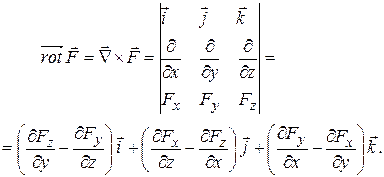
Поверхности вида 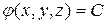, на которых значение силовой функции постоянно и равно заданной константе С, называются поверхностями уровня, или эквипотенциальными поверхностями.

Потенциальная энергия

Потенциальная энергия 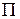тела (и механической системы вообще) складывается из потенциальных энергий отдельных его фрагментов.

Выберем одну из поверхностей уровня и назначим ее поверхностью нулевого уровня потенциальной энергии, т.е. на этой поверхности считается .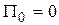

Потенциальная энергия малого фрагмента системы, находящегося в точке 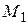поля, равна работе, совершаемой силой 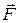при перемещении фрагмента из точки 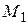на поверхность нулевого уровня: 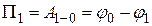. Тогда

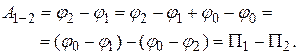
Из сравнения с выражением 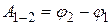следует, что

; .

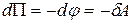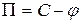3.2.12. Работа силы тяжести. Потенциальная энергия тяжелого тела

Пусть ось 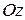направлена вертикально вверх. Работа постоянной силы 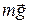, приложенной в центре тяжести тела, равна

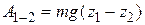, или ,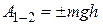

где 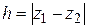- перепад высот между начальным и конечным положениями центра тяжести тела - малая величина сравнительно с радиусом Земли. Из формулы следует, что работа не зависит от формы траектории центра тяжести, следовательно, гравитационное поле потенциально. Потенциальная энергия тела зависит от положения его центра тяжести: 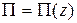. Пусть 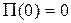; тогда .

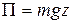Пусть 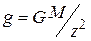, где 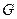- гравитационная постоянная, М – масса Земли, 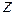- расстояние от центра Земли до центра тяжести тела. Пусть 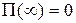; тогда .

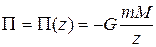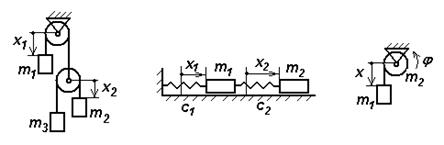
Пример. Пусть механическая система (рис. 10,а) состоит из трех тел массами 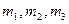, невесомых нерастяжимых нитей и невесомых блоков. Она имеет 2 степени свободы; назначаем обобщенные координаты 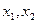, отсчитываемые от точек схода нитей. Потенциальная энергия системы есть функция 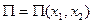. Пусть 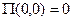; тогда

.

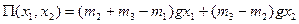3.2.13. Работа упругой силы. Потенциальная энергия упругого элемента

Пусть упругий элемент механической системы (напр., пружина) деформируется в соответствии с законом Гука (см. п. 3.1.8). Работа упругой силы определяется формулой

,

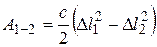где с – коэффициент упругости, 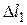- начальная деформация, 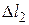- конечная деформация пружины. Введем координату 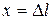, так что 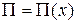, и пусть 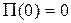. Тогда потенциальная энергия пружины .

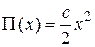Пример. Механическая система (рис. 10,б) состоит из двух тел массами 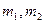, перемещающихся по горизонтальной направляющей, и невесомых пружин, имеющих упругие параметры 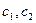. Назначаем обобщенные координаты 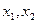, означающие абсолютные смещения тел из их положений равновесия (когда пружины не деформированы). Здесь потенциальная энергия 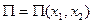. Положим 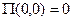; тогда получим, что

-

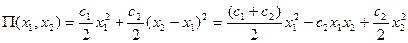- квадратичная форма относительно обобщенных координат.

а б в

Рис. 10. Механические системы с двумя и с одной степенью свободы