Понятие интеллектуальной системы. Типичные задачи ИС.

Примеры задач ИС: предсказания ухода клиентов, задача классификации, предсказания ухода клиентов, ранжирования, кластеризации и т.п.

Символьное моделирование мыслительных процессов

Анализируя историю ИИ, можно выделить такое обширное направление как моделирование рассуждений. Долгие годы развитие этой науки двигалось именно по этому пути, и теперь это одна из самых развитых областей в современном ИИ. Моделирование рассуждений подразумевает создание символьных систем, на входе которых поставлена некая задача, а на выходе требуется её решение. Как правило, предлагаемая задача уже формализована, то есть переведена в математическую форму, но либо не имеет алгоритма решения, либо он слишком сложен, трудоёмок и т. п. В это направление входят: доказательство теорем, принятие решений и теория игр, планирование и диспетчеризация, прогнозирование.

Работа с естественными языками

Немаловажным направлением является обработка естественного языка, в рамках которого проводится анализ возможностей понимания, обработки и генерации текстов на «человеческом» языке. В рамках этого направления ставится цель такой обработки естественного языка, которая была бы в состоянии приобрести знание самостоятельно, читая существующий текст, доступный по Интернету. Некоторые прямые применения обработки естественного языка включают информационный поиск (в том числе, глубокий анализ текста) и машинный перевод.

Представление и использование знаний

Направление инженерия знаний объединяет задачи получения знаний из простой информации, их систематизации и использования. Это направление исторически связано с созданием экспертных систем — программ, использующих специализированные базы знаний для получения достоверных заключений по какой-либо проблеме.

Производство знаний из данных — одна из базовых проблем интеллектуального анализа данных. Существуют различные подходы к решению этой проблемы, в том числе — на основе нейросетевой технологии, использующие процедуры вербализации нейронных сетей.

Машинное обучение

Проблематика машинного обучения касается процесса самостоятельного получения знаний интеллектуальной системой в процессе её работы. Это направление было центральным с самого начала развития ИИ. В 1956 году, на Дартмундской летней конференции, Рей Соломонофф написал отчёт о вероятностной машине, обучающейся без учителя, назвав её: «Индуктивная машина вывода»

Робототехника

Области робототехники и искусственного интеллекта тесно связаны друг с другом. Интегрирование этих двух наук, создание интеллектуальных роботов составляют ещё одно направление ИИ. Интеллектуальность требуется роботам, чтобы манипулировать объектами, выполнять навигацию с проблемами локализации (определять местонахождение, изучать ближайшие области) и планировать движение (как добраться до цели). Примером интеллектуальной робототехники могут служить игрушки-роботы Pleo, AIBO, QRIO.

Применение

Некоторые из самых известных ИИ-систем:

• Deep Blue — победил чемпиона мира по шахматам. Матч Каспаров против суперЭВМ не принёс удовлетворения ни компьютерщикам, ни шахматистам, и система не была признана Каспаровым (подробнее см. Человек против компьютера). Затем линия суперкомпьютеров IBM проявилась в проектах brute force BluGene (молекулярное моделирование) и моделирование системы пирамидальных клеток в швейцарском центре Blue Brain.
• Watson — перспективная разработка IBM, способная воспринимать человеческую речь и производить вероятностный поиск, с применением большого количества алгоритмов. Для демонстрации работы Watson принял участие в американской игре «Jeopardy!», аналога «Своей игры» в России, где системе удалось выиграть в обеих играх.
• MYCIN — одна из ранних экспертных систем, которая могла диагностировать небольшой набор заболеваний, причем часто так же точно, как и доктора.
• 20Q — проект, основанный на идеях ИИ, по мотивам классической игры «20 вопросов». Стал очень популярен после появления в Интернете на сайте 20q.net.
• Распознавание речи. Системы такие как ViaVoice способны обслуживать потребителей.
• Роботы в ежегодном турнире RoboCup соревнуются в упрощённой форме футбола.

Банки применяют системы искусственного интеллекта (СИИ) в страховой деятельности (актуарная математика), при игре на бирже и управлении собственностью. Методы распознавания образов (включая, как более сложные и специализированные, так и нейронные сети) широко используют при оптическом и акустическом распознавании (в том числе текста и речи), медицинской диагностике, спам-фильтрах, в системах ПВО (определение целей), а также для обеспечения ряда других задач национальной безопасности.

Разработчики компьютерных игр применяют ИИ в той или иной степени проработанности. Это образует понятие «Игровой искусственный интеллект». Стандартными задачами ИИ в играх являются нахождение пути в двумерном или трёхмерном пространстве, имитация поведения боевой единицы, расчёт верной экономической стратегии и так далее.

Примеры используемых библиотек для реализации на практике ИС. Краткая характеристика этих библиотек.

PyBrain — одна из лучших Python библиотек для изучения и реализации большого количества разнообразных алгоритмов связанных с нейронными сетями. Являет собой удачный пример совмещения компактного синтаксиса Python с хорошей реализацией большого набора различных алгоритмов из области машинного интеллекта.

Предназначен для:

• Исследователей — предоставляет единообразную среду для реализации различных алгоритмов, избавляя от потребности в использовании десятков различных библиотек. Позволяет сосредоточится на самом алгоритме а не особенностях его реализации.
• Студентов — с использованием PyBrain удобно реализовать домашнее задание, курсовой проект или вычисления в дипломной работе. Гибкость архитектуры позволяет удобно реализовывать разнообразные сложные методы, структуры и топологии.
• Лекторов — обучение методам Machine Learning было одной из основных целей при создании библиотеки. Авторы будут рады, если результаты их труда помогут в подготовке грамотных студентов и специалистов.
• Разработчиков — проект Open Source, поэтому новым разработчикам всегда рады.

PyBrian представляет собой модульную библиотеку предназначенную для реализации различных алгоритмов машинного обучения на языке Python. Основной его целью является предоставление исследователю гибких, простых в использовании, но в то же время мощных инструментов для реализации задач из области машинного обучения, тестирования и сравнения эффективности различных алгоритмов.
Название PyBrain является аббревиатурой от английского: Python-Based Reinforcement Learning, Artificial Intelligence and Neural Network Library.
Как сказано на одном сайте: PyBrain — swiss army knife for neural networking ( PyBrain — это швейцарский армейский нож в области нейро-сетевых вычислений).

Библиотека построена по модульному принципу, что позволяет использовать её как студентам для обучения основам, так и исследователям, нуждающимся в реализации более сложных алгоритмов. Общая структура процедуры её использования приведена на следующей схеме:

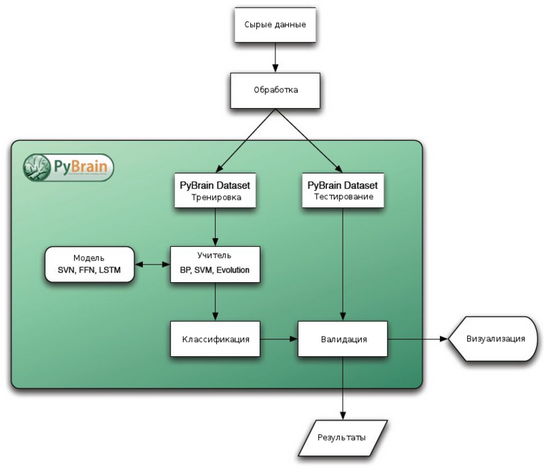
PyBrain оперирует сетевыми структурами, которые могут быть использованы для построения практически всех поддерживаемых библиотекой сложных алгоритмов. В качестве примера можно привести:

• Сети прямого распространения, включая Deep Belief Networks и Restricted Boltzmann Machines (RBM)
• Рекуррентные нейронные сети ( Recurrent networks — RNN), включая архитектуру Long Short-Term Memory (LSTM)
• Multi-Dimensional Recurrent Networks (MDRNN)
• Сети Кохонена / Self-Organizing Maps
• Reservoirs
• Нейронная сеть Коско / Bidirectional networks
• Создание топологий собственной структуры

(статья https://habrahabr.ru/post/148407/)

В процессе создания игр разработчик AI сталкивается с разными нетривиальными проблемами. Как правило, ответы не лежат на поверхности. Для выбора наиболее подходящего способа решения проблемы нужно знать специфику множества алгоритмов, применяемых для реализации искусственного интеллекта. Иногда, столкнувшись со сложной задачей, программист пытается решить ее силовым методом, через известные приемы, например, до бесконечности расширяя конечные автоматы, и тем самым добивается желаемого геймплея. При таком подходе уходит много сил и полученное поведение персонажей или объектов не всегда отличается элегантностью и естественностью. Решение можно искать и путем прочтения большого количества книг по искусственному интеллекту. Однако, даже будучи прочитанной, сухая теория не всегда приходит на помощь. Да и сам подход чтения всего подряд не удобен, особенно в ситуации жестких временных графиков: большинство прочитанного не имеет отношения к стоящим проблемам или новые идеи, возникающие при чтении, первоначально показавшись многообещающими, после мучительного процесса их воплощения, дают неудовлетворительный результат.

Оценить степень пригодности алгоритмов можно было бы на примерах их реализации в играх. Вообще, многие программисты считают, что учиться тем или иным приемам программирования лучше всего на основе работающего кода. Однако, хороших демонстрационных примеров реализации алгоритмов AI довольно немного. Для целей обучения и экспериментов, хотелось бы представить библиотеку FEAR [http://fear.sourceforge.net/] (Flexible Embodied Animat aRchitecture - библиотека настраиваемой архитектуры материализованных анимированных персонажей) (к сожалению, сайт библиотеки последнее время выдает ошибку), версия 0.4 которой вышла в начале 2005. Эта библиотека дает возможность изучать большинство существующих подходов искусственного интеллекта через реализацию поведения ботов для игры Quake 2. В версии 0.4, FEAR, наконец, стала по настоящему стабильной. Помимо улучшения модульности и устойчивости ядра, непосредственно реализующего алгоритмы AI, добавлено, по сравнению с предыдущими версиями, большое количество примеров. Примеры включают показ того, как реализуется реактивное поведение, как применять конечные автоматы, нейронные сети, генетические алгоритмы, деревья решения и даже демонстрируется реализация эмоций ботов на базе многоуровневых конечных автоматов. Иначе говоря, раскрыты практически все аспекты AI, встречающиеся в практике разработки игр.

Коснувшись достоинств, необходимо упомянуть то, что установка, запуск работающих примеров и начало их отладки, потребует довольно значительный усилий. Именно с целью ускорить процесс установки и освоения библиотеки написана данная статья.

В статье описываются шаги, которые необходимы для начала полноценной работы с библиотекой с использованием среды Visual Studio 8.0, однако описание позволит ускорить начало работы и для пользователей, имеющих версии Visual Studio 7.0 и 7.1.

FEAR можно использовать и с другими компиляторами. Желающие смогут разобраться с альтернативами, воспользовавшись документацией к библиотеке и системой построения проектов SCONS [http://www.scons.org/], для которой в инсталляцию библиотеки включены соответствующие скрипты.

Задача распознавания образов (классификации). Примеры задач распознавания образов и основные подходы к ее решению. Отличие задачи кластеризации от задачи классификации.

Признаки и классификаторы

Измерения, используемые для классификации образов, называются признаками. Признак – это некоторое количественное измерение объекта произвольной природы. Совокупность признаков, относящихся к одному образу, называется вектором признаков. Вектора признаков принимают значения в пространстве признаков. В рамках задачи распознавания считается, что каждому образу ставится в соответствие единственное значение вектора признаков и наоборот: каждому значению вектора признаков соответствует единственный образ.

Классификатором или решающим правилом называется правило отнесения образа к одному из классов на основании его вектора признаков.

Пример 1. Иллюстрация понятий признаков и классификатора и идеи распознавания (классификации). Рассмотрим задачу диагностики печени по результатам инструментального исследования (рис.1.1). Доброкачественные (левый рисунок – класс A) и злокачественные (правый рисунок – класс B) изменения дают разную картину. Предположим, что имеется несколько препаратов в базе данных, про которые известна их принадлежность к классам A и B (правильная классификация). Очевидно, что образцы отличаются интенсивностью точек изображения. В качестве вектора признаков выберем пару: среднее значение ( ) и среднеквадратичное отклонение ( ) интенсивности в изображении.

Рис. 1.1.Образы-прецеденты, соответствующие классу A (слева) и B (справа)

Рис. 1.2.Распределение векторов признаков прецедентах класса A (кружки) и класса B (крестики). Признаки - средние значения и средние отклонения яркости в образах. Прямая линия разделяет вектора из разных классов

На рис.1.2 представлены изображения этих образов в пространстве признаков. Точки, соответствующие прецедентам разных классов, разделяются прямой линией. Классификация неизвестного образа (соответствующая точка изображена звездочкой) состоит в проверке положения точки относительно этой разделяющей прямой.

Практическая разработка системы классификации осуществляется по следующей схеме (рис.1.3). В процессе разработки необходимо решить следующие вопросы.

1. Как выбрать вектора признаков? Задача генерации признаков – это выбор тех признаков, которые с достаточной полнотой (в разумных пределах) описывают образ.
2. Какие признаки наиболее существенны для разделения объектов разных классов? Задача селекции признаков – отбор наиболее информативных признаков для классификации.
3. Как построить классификатор? Задача построения классификатора – выбор решающего правила, по которому на основании вектора признаков осуществляется отнесение объекта к тому или иному классу.
4. Как оценить качество построенной системы классификации? Задача количественной оценки системы (выбранные признаки + классификатор) с точки зрения правильности или ошибочности классификации.

Рис. 1.3.Основные элементы построения системы распознавания образов (классификации)

(Статья http://www.intuit.ru/studies/courses/2265/243/lecture/6241?page=1)

Задача классификации

Классификация является наиболее простой и одновременно наиболее часто решаемой задачей Data Mining. Ввиду распространенности задач классификации необходимо четкое понимания сути этого понятия.

Приведем несколько определений.

Классификация - системное распределение изучаемых предметов, явлений, процессов по родам, видам, типам, по каким-либо существенным признакам для удобства их исследования; группировка исходных понятий и расположение их в определенном порядке, отражающем степень этого сходства.

Классификация - упорядоченное по некоторому принципу множество объектов, которые имеют сходные классификационные признаки (одно или несколько свойств), выбранных для определения сходства или различия между этими объектами.

Классификация требует соблюдения следующих правил:

• в каждом акте деления необходимо применять только одно основание;
• деление должно быть соразмерным, т.е. общий объем видовых понятий должен равняться объему делимого родового понятия;
• члены деления должны взаимно исключать друг друга, их объемы не должны перекрещиваться;
• деление должно быть последовательным.

Различают:

• вспомогательную (искусственную) классификацию, которая производится по внешнему признаку и служит для придания множеству предметов (процессов, явлений) нужного порядка;
• естественную классификацию, которая производится по существенным признакам, характеризующим внутреннюю общность предметов и явлений. Она является результатом и важным средством научного исследования, т.к. предполагает и закрепляет результаты изучения закономерностей классифицируемых объектов.

В зависимости от выбранных признаков, их сочетания и процедуры деления понятий классификация может быть:

• простой - деление родового понятия только по признаку и только один раз до раскрытия всех видов. Примером такой классификации является дихотомия, при которой членами деления бывают только два понятия, каждое из которых является противоречащим другому (т.е. соблюдается принцип: "А и не А");
• сложной - применяется для деления одного понятия по разным основаниям и синтеза таких простых делений в единое целое. Примером такой классификации является периодическая система химических элементов.

Под классификацией будем понимать отнесение объектов (наблюдений, событий) к одному из заранее известных классов.

Классификация - это закономерность, позволяющая делать вывод относительно определения характеристик конкретной группы. Таким образом, для проведения классификации должны присутствовать признаки, характеризующие группу, к которой принадлежит то или иное событие или объект (обычно при этом на основании анализа уже классифицированных событий формулируются некие правила).

Классификация относится к стратегии обучения с учителем (supervised learning), которое также именуют контролируемым или управляемым обучением.

Задачей классификации часто называют предсказание категориальной зависимой переменной (т.е. зависимой переменной, являющейся категорией) на основе выборки непрерывных и/или категориальных переменных.

Например, можно предсказать, кто из клиентов фирмы является потенциальным покупателем определенного товара, а кто - нет, кто воспользуется услугой фирмы, а кто - нет, и т.д. Этот тип задач относится к задачам бинарной классификации, в них зависимая переменная может принимать только два значения (например, да или нет, 0 или 1).

Другой вариант классификации возникает, если зависимая переменная может принимать значения из некоторого множества предопределенных классов. Например, когда необходимо предсказать, какую марку автомобиля захочет купить клиент. В этих случаях рассматривается множество классов для зависимой переменной.

Классификация может быть одномерной (по одному признаку) и многомерной (по двум и более признакам).

Многомерная классификация была разработана биологами при решении проблем дискриминации для классифицирования организмов. Одной из первых работ, посвященных этому направлению, считают работу Р. Фишера (1930 г.), в которой организмы разделялись на подвиды в зависимости от результатов измерений их физических параметров. Биология была и остается наиболее востребованной и удобной средой для разработки многомерных методов классификации.

Процесс классификации

Цель процесса классификации состоит в том, чтобы построить модель, которая использует прогнозирующие атрибуты в качестве входных параметров и получает значение зависимого атрибута. Процесс классификации заключается в разбиении множества объектов на классы по определенному критерию.

Задача кластеризации

Только что мы изучили задачу классификации, относящуюся к стратегии "обучение с учителем".

В этой части лекции мы введем понятия кластеризации, кластера, кратко рассмотрим классы методов, с помощью которых решается задача кластеризации, некоторые моменты процесса кластеризации, а также разберем примеры применения кластерного анализа.

Задача кластеризации сходна с задачей классификации, является ее логическим продолжением, но ее отличие в том, что классы изучаемого набора данных заранее не предопределены.

Синонимами термина " кластеризация " являются "автоматическая классификация ", "обучение без учителя" и "таксономия".

Кластеризация предназначена для разбиения совокупности объектов на однородные группы ( кластеры или классы). Если данные выборки представить как точки в признаковом пространстве, то задача кластеризации сводится к определению "сгущений точек".

Цель кластеризации - поиск существующих структур.

Кластеризация является описательной процедурой, она не делает никаких статистических выводов, но дает возможность провести разведочный анализ и изучить "структуру данных".

Само понятие " кластер " определено неоднозначно: в каждом исследовании свои " кластеры ". Переводится понятие кластер (cluster) как "скопление", "гроздь".

Кластер можно охарактеризовать как группу объектов, имеющих общие свойства.

Характеристиками кластера можно назвать два признака:

• внутренняя однородность;
• внешняя изолированность.

Вопрос, задаваемый аналитиками при решении многих задач, состоит в том, как организовать данные в наглядные структуры, т.е. развернуть таксономии.

Наибольшее применение кластеризация первоначально получила в таких науках как биология, антропология, психология. Для решения экономических задач кластеризация длительное время мало использовалась из-за специфики экономических данных и явлений.

В таблице 5.2 приведено сравнение некоторых параметров задач классификации и кластеризации.

Таблица 5.2. Сравнение классификации и кластерзации
Характеристика	Классификация	Кластеризация
Контролируемость обучения	Контролируемое обучение	Неконтролируемое обучение
Стратегия	Обучение с учителем	Обучение без учителя
Наличие метки класса	Обучающее множество сопровождается меткой, указывающей класс, к которому относится наблюдение	Метки класса обучающего множества неизвестны
Основание для классификации	Новые данные классифицируются на основании обучающего множества	Дано множество данных с целью установления существования классов или кластеров данных

На рис. 5.7 схематически представлены задачи классификации и кластеризации.

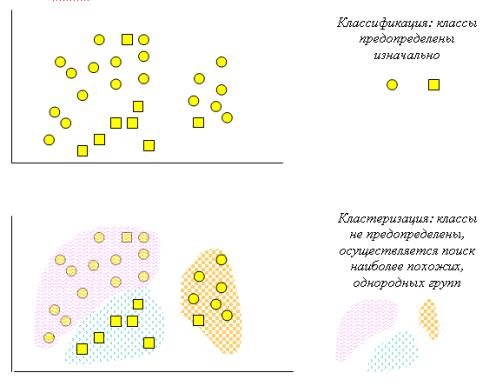
Рис. 5.7.Сравнение задач классификации и кластеризации

6 Способы определения классов объектов: перечисление, задание общих свойств. Примеры.

Разбиение рассматриваемого множества объектов на классы Ω_i может быть задано следующими способами:

1. Перечисление.Каждый класс задаётся путём прямого указания его членов.Такойподход используется в том случае, если доступна полная априорная информация о всех возможных объектах распознавания. Предъявляемые системе образы сравниваются с заданными описаниями представителей классов и относятся к тому классу, которому принадлежат наиболее сходные с ними образцы. Такой подход называют методом сравнения

с эталоном.Его недостатком является слабая устойчивость к шумам и искажениям враспознаваемых образах.

Пример.Распознавание машинопечатного шрифта.Все символы имеют чёткозаданное шрифтом начертание. Следовательно, необходимо обучить систему путём прямого указания изображений всех распознаваемых символов (т.е. путём задания эталонов):

АБ В ..... а б в ... 1 2 3 ....

Необходимо отметить, что если предполагается распознавание курсивного, полужирного или иного начертания символов шрифта, то при таком подходе будет необходимо представить каждый вариант начертания каждого символа. Это связано с характером процесса распознавания : каждый распознаваемый объект попиксельно сравнивается поочерёдно со всеми известными системе эталонами. Кроме того, способность распознавания линейных трансформаций данных эталонов требует определённых усилий на этапе предобработки.

2. Задание общих свойств.Класс задаётся указанием некоторых признаков,присущихвсем его членам. Распознаваемый объект в таком случае не сравнивается напрямую с группой эталонных объектов. В его первичном описании выделяются значения определённого набора признаков, которые затем сравниваются с заданными признаками классов. При этом для каждого признака может задаваться требование либо к его наличию/отсутствию, либо к нахождению его числового значения в установленных пределах. Такой подход называется сопоставлением по признакам . Он экономичнее метода сравнения с эталоном в вопросе количества памяти, необходимой для хранения описаний классов. Кроме того, он допускает некоторую вариативность распознаваемых образов. Однако, главной сложностью является определение полного набора признаков, точно отличающих членов одного класса от членов всех остальных.

Пример.Распознавание цифр почтовых индексов[17].Рассматривается следующий наборраспознаваемых символов (рис. 2):

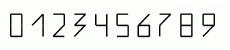
Рисунок 2: Цифры почтовых индексов

Каждый из показанных символов представляет класс распознаваемых объектов — одну из цифр. Все эти изображения построены по одному принципу — с помощью комбинирования вертикальных, горизонтальных и диагональных сегментов в определённых позициях знакомест. Для описания классов предлагаются следующие признаки:

x₁ —количество вертикальных линий минимального размера; x₂ —количество горизонтальных линий; x₃ —количество наклонных линий;

x₄ —количество горизонтальных линий снизу объекта.

С помощью этих признаков можно следующим образом задать классы цифр:

	x1	x2	x3	x4

Заметим, что набор выбранных признаков не является единственно возможным. Качество распознавания во многом зависит от того, насколько удачно разработчиком системы выбран набор признаков [8].

Дополнение к вопросу:

Перечисление

– Каждый класс задаётся путём прямого указания его членов;

– Используется, если доступна полная априорная информация о всех возможных объектах распознавания;

– Предъявляемые системе образы сравниваются с заданными описаниями представителей классов и относятся к тому классу, которому принадлежат наиболее сходные с ними образцы – метод сравнения с эталоном;

– Применим, к примеру, при распознавании машинопечатных символов определённого шрифта;

– Недостаток – слабая устойчивость к шумам и искажениям в распознаваемых образах.

Задание общих свойств:

– Класс задаётся указанием некоторых признаков, присущих всем его членам;

– В его первичном описании распознаваемого объекта выделяются значения определённого набора признаков, которые затем сравниваются с заданными признаками классов - сопоставление по признакам.

– Такой метод экономичнее метода сравнения с эталоном в вопросе количества памяти, необходимой для хранения описаний классов.

– Допускает некоторую вариативность распознаваемых образов.

– Недостаток – сложность определения полного набора признаков, точно отличающих членов одного класса от членов всех остальных.

7. Непараметрические методы распознавания образов. Алгоритм распознавания по образцу. Проблема выбора метрики.

Распознавание образов (объектов, сигналов, ситуаций, явлений или процессов) - задача идентификации объекта или определения каких-либо его свойств по его изображению (оптическое распознавание) или аудиозаписи (акустическое распознавание) и другим характеристикам.

Одним из базовых является не имеющее конкретной формулировки понятие множества. В компьютере множество представляется набором неповторяющихся однотипных элементов. Слово "неповторяющихся" означает, что какой-то элемент в множестве либо есть, либо его там нет. Универсальное множество включает все возможные для решаемой задачи элементы, пустое не содержит ни одного.

Образ - классификационная группировка в системе классификации, объединяющая (выделяющая) определенную группу объектов по некоторому признаку. Образы обладают характерным свойством, проявляющимся в том, что ознакомление с конечным числом явлений из одного и того же множества дает возможность узнавать сколь угодно большое число его представителей. Образы обладают характерными объективными свойствами в том смысле, что разные люди, обучающиеся на различном материале наблюдений, большей частью одинаково и независимо друг от друга классифицируют одни и те же объекты. В классической постановке задачи распознавания универсальное множество разбивается на части-образы. Каждое отображение какого-либо объекта на воспринимающие органы распознающей системы, независимо от его положения относительно этих органов, принято называть изображением объекта, а множества таких изображений, объединенные какими-либо общими свойствами, представляют собой образы (более подробно можно ознакомиться на сайте http://www.codenet.ru).

Методика отнесения элемента к какому-либо образу называется решающим правилом. Еще одно важное понятие - метрика, способ определения расстояния между элементами универсального множества. Чем меньше это расстояние, тем более похожими являются объекты (символы, звуки и др.) - то, что мы распознаем. Обычно элементы задаются в виде набора чисел, а метрика - в виде функции. От выбора представления образов и реализации метрики зависит эффективность программы, один алгоритм распознавания с разными метриками будет ошибаться с разной частотой.

Обучением обычно называют процесс выработки в некоторой системе той или иной реакции на группы внешних идентичных сигналов путем многократного воздействия на систему внешней корректировки. Такую внешнюю корректировку в обучении принято называть "поощрениями" и "наказаниями". Механизм генерации этой корректировки практически полностью определяет алгоритм обучения. Самообучение отличается от обучения тем, что здесь дополнительная информация о верности реакции системе не сообщается.

Адаптация - это процесс изменения параметров и структуры системы, а возможно - и управляющих воздействий, на основе текущей информации с целью достижения определенного состояния системы при начальной неопределенности и изменяющихся условиях работы.

Обучение - это процесс, в результате которого система постепенно приобретает способность отвечать нужными реакциями на определенные совокупности внешних воздействий, а адаптация - это подстройка параметров и структуры системы с целью достижения требуемого качества управления в условиях непрерывных изменений внешних условий.

Примеры задач распознавания образов:
- Распознавание букв;
- Распознавание штрих-кодов;
- Распознавание автомобильных номеров;
- Распознавание лиц и других биометрических данных;
- Распознавание речи.

8. Статистический подход в задаче распознавания образов. Использование правила Байеса.

История развития

Основы теории игр зародились еще в 18 веке, с началом эпохи просвящения и развитием экономической теории. Впервые математические аспекты и приложения теории были изложены в классической книге 1944 года Джона фон Неймана и Оскара Моргенштерна «Теория игр и экономическое поведение». Первые концепции теории игр анализировали антагонистические игры, когда есть проигравшие и выигравшие за их счет игроки. Не смотря на то, что теория игр рассматривала экономические модели, вплоть до 50-х годов 20 века она была всего лишь математической теорией. После, в результате резкого скачка экономики США после второй мировой войны, и, как следствие, большего финансирования науки, начинаются попытки практического применения теории игр в экономике, биологии, кибернетике, технике, антропологии. Во время Второй мировой войны и сразу после нее теорией игр серьезно заинтересовались военные, которые увидели в ней мощный аппарат для исследования стратегических решений. В начале 50-х Джон Нэш разрабатывает методы анализа, в которых все участники или выигрывают, или терпят поражение. Эти ситуации получили названия «равновесие по Нэшу». По его теории, стороны должны использовать оптимальную стратегию, что приводит к созданию устойчивого равновесия. Игрокам выгодно сохранять это равновесие, так как любое изменение ухудшит их положение. Эти работы Нэша сделали серьезный вклад в развитие теории игр, были пересмотрены математические инструменты экономического моделирования. Джон Нэш показывает, что классический подход к конкуренции А.Смита, когда каждый сам за себя, неоптимален. Более оптимальны стратегии, когда каждый старается сделать лучше для себя, делая лучше для других. За последние 20 — 30 лет значение теории игр и интерес значительно растет, некоторые направления современной экономической теории невозможно изложить без применения теории игр.Большим вкладом в применение теории игр стала работа Томаса Шеллинга, нобелевского лауреата по экономике 2005 г. «Стратегия конфликта».

Типы игр

Кооперативная\некооперативная игра

Кооперативной игрой является конфликт, в котором игроки могут общаться между собой и объединяться в группы для достижения наилучшего результата. Примером кооперативной игры можно считать карточную игру Бридж, где очки каждого игрока считаются индивидуально, но выигрывает пара, набравшая наибольшую сумму. Из двух типов игр, некооперативные описывают ситуации в мельчайших деталях и выдают более точные результаты. Кооперативные рассматривают процесс игры в целом. Не смотря на то, что эти два вида противоположны друг другу, вполне возможно объединение стратегий, которое может принести больше пользы, чем следование какой-либо одной.

С нулевой суммой и с ненулевой суммой

Игрой с нулевой суммой называют игру, в которой выигрыш одного игрока равняется проигрышу другого. Например банальный спор: если вы выиграли сумму N, то кто-то эту же сумму N проиграл. В игре же с ненулевой суммой может изменяться общая цена игры, таким образом принося выгоду одному игроку, не отнимаю ее цену у другого. В качестве примера здесь отлично подойдут шахматы: превращая пешку в ферзя игрок А увеличивает общую сумму своих фигур, при этом не отнимая ничего у игрока Б. В играх с ненулевой суммой проигрыш одного из игроков не является обязательным условием, хотя такой исход и не исключается.

Параллельные и последовательные

Параллельной является игра, в которой игроки делают ходы одновременно, либо ход одного игрока неизвестен другому, пока не завершится общий цикл. В последовательной игре каждый игрок вл