Дифференциальные уравнения движения Навье – Стокса

При движении реальной (вязкой) жидкости в потоке жидкости помимо сил давления и тяжести действуют также силы трения.

Действе сил трения Т на выделенный в потоке вязкой жидкости элементарный параллелепипед проявляется в возникновении на его поверхности касательных напряжений. Рассмотрим первоначально простой случай одномерного плоского потока капельной жидкости в направлении оси х, когда проекция скорости капельной жидкости в направлении оси х, когда проекция скорости ω_х зависит только от расстояния z до горизонтальной плоскости отсчета.

В этих условиях касательные напряжения возникают лишь на поверхностях dF верхней и нежней граней элементарного параллелепипеда, причем dF = dxdy. Если касательное напряжение на нижней грани параллелепипеда равно τ, то на верхней оно составит .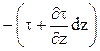

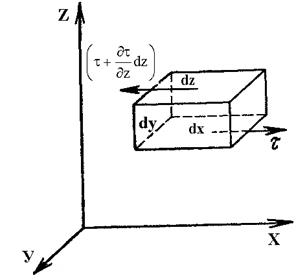При этом направления касательных напряжений на нижней и верхней гранях обусловлены, например, тем, что более медленные вышележащие слои жидкости затормаживают слой, в котором находится параллелепипед, а более быстрые нижележащие слои «разгоняют» его. Производная 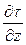выражает изменение касательного напряжения вдоль оси z в точках, лежащих на нижней грани параллелепипеда, а 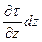представляет собой изменение этого напряжения вдоль всей длины dz ребра параллелепипеда.

Тогда проекция равнодействующей сил трения на ось х

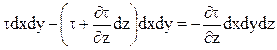
В общем случае проекция равнодействующей сил трения на ось х примет вид

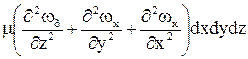
Сумму вторых производных по осям координат называют оператором Лапласа:

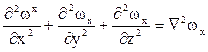
Следовательно

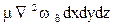
Соответственно проекции равнодействующей сил трения:

на ось у

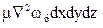
на ось х

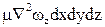
Проекции на оси координат равнодействующей всех сил (тяжести, давления и трения), действующих на элементарный объем капельной жидкости (с учетом проекций сил тяжести и давления, полученных при выводе уравнений Эйлера), составляют:

на ось х

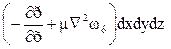
на ось у

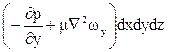
на ось z

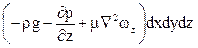
Согласно основного принципа динамики (сумма проекций сил на оси координат равны произведению массы жидкости 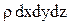на проекции ускорения на оси координат).

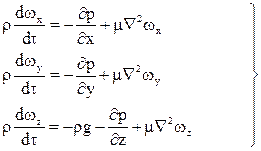(1)

Уравнения (1) представляют собой уравнения Навье – Стокса, описывающие движение вязкой капельной жидкости.

Интегральная форма представлена уравнением Пуазейля – характеризующие ламинарное установившееся.

Уравнение Бернулли

Решение уравнений движения Эйлера для установившегося потока приводит к одному из наиболее важных и широко используемых уравнений гидродинамики – уравнению Бернулли.

Для двух поперечных сечений 1 и 2 потока

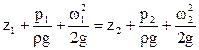(1)

Уравнение Бернулли для идеальной жидкости.

1 – называют полным гидродинамическим напором.

Следовательно, согласно уравнению Бернулли, для всех поперечных сечений установившегося потока идеальной жидкости величина гидродинамического напора остается неизменной.

z – нивелирная высота, называемая также геометрическим напором, представляет собой удельную потенциальную энергию положения в данной точке.

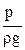– статический или пьезометрический напор, характеризует удельную потенциальную энергию давления в данной точке.

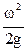– скоростной или динамический напор, характеризует удельную кинетическую энергию в данной точке.

Уравнение Бернулли является частным случаем закона сохранения энергии и выражает энергетический баланс потока.

Уравнение Бернулли реальных жидкостей

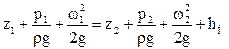
где h_П – потерянный напор, характеризует удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости.

Основы теории подобия

Модель – упрощенное представление о явлениях, происходящих в естественной природе и сохраняющая основные черты происходящего.

Безразмерные масштабные множители, выражающие отношения однородных сходственных величин подобных фигур (или систем), называются константами подобия.

Инвариантом подобия называют безразмерные отношения каких-либо двух размеров одной из фигур, равные отношению сходственных размеров подобной фигуры.

Геометрическое подобие соблюдается при равенстве отношений всех сходственных линейных размеров натуры и модели:

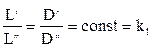
Временное подобие характеризуется тем, что сходственные частицы в геометрически подобных системах, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути за промежутки времени, отношение которых является постоянной величиной:

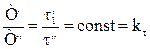
Подобие физических величин предполагает, что для двух сходственных точек, размещенных подобно в пространстве и времени, отношения физических свойств является величинами постоянными:

Первая теорема подобия была сформулирована Ньютоном. Согласно этой теореме, при подобии систем всегда могут быть найдены такие безразмерные комплексы величин, которые для сходственных точек данных систем одинаковы, т.е. подобные явления характеризуются численно равными критериями подобия.

Второй закон Ньютона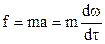

Выделим в подобных системах 2 частицы, движущиеся подобно. В натуре на частицу массой 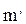действует сила 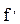сообщая ей ускорение 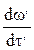; в модели сходственная частица массой 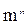под действием силы 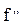приобретает ускорение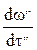

Тогда

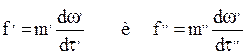
При подобном движении частиц для сходственных точек натуры и модели константы подобия выражаются отношениями:

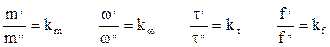
т.е.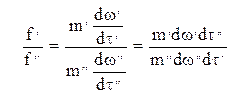

Отношения приращений величин, входящих в константы подобия, можно заменить отношениями самих величин, т.е.

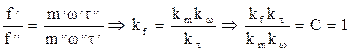
Величину С, составленную их констант подобия, называют индикатором подобия.

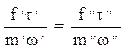
Таким образом, получен безразмерный комплекс величин, значения которого одинаковы для сходственных точек обеих систем. Этот комплекс называют критерием Ньютона

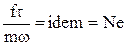
который характеризует отношение действующей на частицу силы к силе инерции.

Достоинства критериев – не имеют размерности и позволяют удобно моделировать процессы упрощенно.

Вторая теорема подобия была доказана Бэкингемом, Федерманом и Афанасьевой-Эренфест. Согласно этой теореме, решение любого дифференциального уравнения, связывающего между собой переменные, влияющие на процесс, может быть представлено в виде зависимости между безразмерными комплексами этих величин, т.е. между критериями подобия.

Если обозначить критерии подобия через 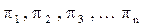, то решение дифференциального уравнения может быть представлено в общем виде:

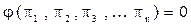
Такие уравнения называют уравнениями в обобщенных переменных или критериальными уравнениями.

Критерии подобия, которые составлены только из величин, входящих в условия однозначности, называют определяющими. Критерии же, включающие также величины, которые не являются необходимыми для однозначной характеристики данного процесса, а сами зависят от этих условий, называют определяемыми.

Из критериального уравнения, представляющего собой функциональную зависимость между критериями подобия, рассчитав предварительно величины определяющих критериев, находят величину определяемого критерия, а из него – численное значение интересующей нас величины. Если определяемым является некоторый критерий π₁ , то .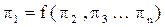

Вторая теорема подобия отвечает на вопрос, как обрабатывать результаты опытов, проведенных на моделях: их надо представлять в виде функциональной зависимости между критериями подобия.

Третья теорема подобия, или теорема М.В.Кирпичева и А.А. Гухмана, формулирует необходимые и достаточные условия подобия: подобны те явления, которые описываются одной и той же системой дифференциальных уравнений и у которых соблюдается подобие условий однозначности.

Таким образом, исследование процессов методом теории подобия должно состоять из следующих элементов:

1. Получив полное математическое описание процесса, т.е. составив дифференциальное уравнение и установив условия однозначности, проводят подобное преобразование этого уравнения и находят критерии подобия.

2. Опытным путем на моделях устанавливают конкретный вид зависимости между критериями подобия, причем полученное обобщенное расчетное уравнение справедливо для всех подобных явлениях в исследованных пределах.

Движение тел в жидкости

При движении тела в жидкости возникают сопротивления, для преодоления которых и обеспечения равномерного движения тела должна быть затрачена определенная энергия. Величина возникающего сопротивления зависит главным образом от режима движения и формы обтекаемого тела.

При ламинарном режиме тело окружено пограничным слоем жидкости и плавно обтекается потоком. Потеря энергии связана с преодолением сопротивления трения. С развитием турбулентности потока все большую роль начинают играть силы инерции. Сила сопротивления R среды движущемуся в ней телу выражена уравнением сопротивления:

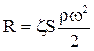(1)

где S – площадь проекции тела на плоскость, перпендикулярную направлению его движения, м² ;

ζ – коэффициент сопротивления среды.

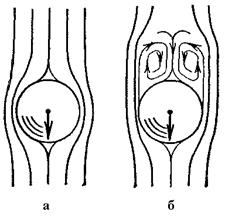а – ламинарный поток

б – турбулентный поток

Отношение R/S представляет собой перепад давлений Δр (Н/м²), преодолеваемый движущимся телом.

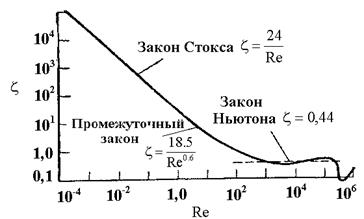
Ламинарный режим закон Стокса Re < 2

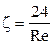
Переходный режим Re = 2 – 500

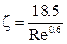
Автомодельный режим закон Ньютона ~ 2·10⁵ > Re < ~ 500

ζ = 0,44 = const

Постановка в уравнение (1) каждого из приведённых выше уравнений для ζ показывает, что для ламинарного режима Re ~ ω для переходного режима Re ~ ω^1,4 , для автомодельного режима Re ~ ω²

Для тел по форме отличных от шарообразных значения коэффициента сопротивления зависит от фактора формы Ф и числа Рейнольдса.

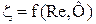здесь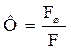

где F_ш – поверхность шара, имеющего тот же объём, что и рассматриваемое тело поверхностью F. Например, для куба Ф = 0,806; для цилиндра высотой, в 10 раз превышающей его радиус, Ф = 0,69.

Закон внутреннего трения Ньютона, согласно которому напряжение внутреннего трения, возникающее между слоями жидкости при её течении, прямо пропорционально градиенту скорости.

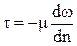кажущейся вязкостью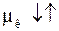

где μ – динамический коэффициент вязкости;

τ – касательное напряжение, напряжение внутреннего трения.

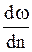– градиент скорости.

Жидкости, подчиняющиеся закону внутреннего трения Ньютона называются нормальными, или ньютоновскими. Однако в промышленной практике приходится иметь дело и с неньютоновскими жидкостями (растворы многих полимеров, густые суспензии, пасты (бингамовские пластичные, псевдопластичные, дилатантные и др.)