Тема 1 Предмет и основные категории статистики

Тема 1 Предмет и основные категории статистики

Краткая история развития статистики.

Предмет статистики и основные разделы.

Тема 2 Статистическое наблюдение

Сущность статистического наблюдения

Формы, виды и способы статистического наблюдения

План статистического наблюдения

Контроль материалов статистического наблюдения. Ошибки статистического наблюдения

1.

Статистическое наблюдение - первая стадия статистического исследования, представляющего собой научно-организованный по единой программе учет фактов, характеризующих явления и процессы общественной жизни.

Наблюдение является фундаментом статистического исследования. В процессе наблюдения формируются данные, которые на последующих этапах исследования подвергаются обработке и анализу. Организация статистического наблюдения предполагает определение объекта и единицы наблюдения, разработки программы и организационного плана проведения наблюдения.

Объект статистического наблюдения- это совокупность общественных явлений и процессов, которые полежат данному статистическому наблюдению.

Изучение объекта статистического наблюдения предполагает выделение в его составе отдельных единиц.

Единицей статистического наблюденияявляется составной элемент объекта наблюдения, являющийся носителем признаков, подлежащих регистрации в процессе данного наблюдения. От единицы наблюдения следует отличать отчетную единицу.

Отчетная единица- это источник сведений о единицах наблюдения.

Программа статистического наблюдения представляет собой перечень вопросов, по которым нужно получить сведения в отношении каждой исследуемой единицы в процессе наблюдения.

2.

В статистической практике используются две организационные формы наблюдения – отчетность и специальное статистическое обследование.

Отчетность – это такая организационная форма, при которой единицы наблюдения представляют сведения о своей деятельности в виде формуляров регламентированного образца.

Особенность отчетности состоит в том, что она обязательна, документально обоснована и юридически подтверждена подписью руководителя.

Примером второй формы наблюдения – специального статистического обследования – является проведение переписей населения.

В зависимости от задач статистического исследования и характера изучаемого явления учет фактов можно производить:

- систематически, постоянно охватывая факты по мере их возникновения – это будет текущее наблюдение (отчетность);

- регулярно, но не постоянно, а через определенные промежутки времени – это будет периодическое наблюдение (переписи населения).

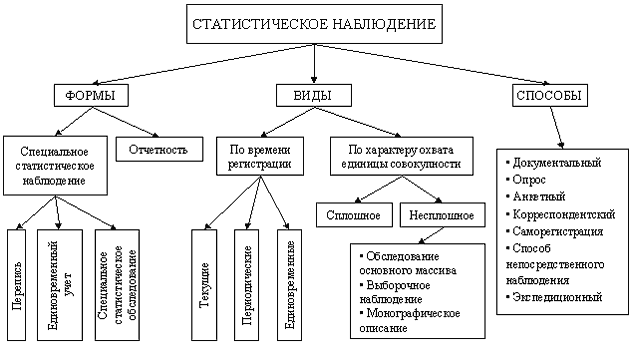
Рис. 1. Формы, виды и способы статистического наблюдения

С точки зрения полноты охвата фактов статистическое наблюдение может быть сплошным и несплошным. Сплошное наблюдение представляет собой полный учет всех единиц изучаемой совокупности. Несплошное наблюдение организуют как учет части единиц совокупности, на основе которой можно получить обобщающую характеристику всей совокупности. К видам несплошного наблюдения относятся: способ основного массива, выборочные наблюдения, монографические описания.

При непосредственном учете фактов сведения получают путем личного учета единиц совокупности: пересчета, взвешивания, измерения и т.д.

Документальный способ сбора статистической информации базируется на систематических записях в первичных документах, подтверждающих тот или иной факт.

В ряде случаев для заполнения статистических формуляров прибегают к опросу населения, который может быть произведен экспедиционным, анкетным или корреспондентским способом.

Существуют различные способы формирования выборочной совокупности. Это, во-первых, индивидуальный отбор, включающий такие разновидности, как собственно случайный, механический, стратифицированный, и, во-вторых, серийный, или гнездовой, отбор.

3.

Организационный план статистического наблюдения представляет собой перечень мероприятий, необходимых для успешного выполнения работы по сбору и обработке материалов, с указанием сроков и исполнителей.

Это основной документ, в котором отображаются важнейшие вопросы организации и про­ведения намеченных мероприятий. В организационном плане ука­зываются: органы наблюдения, время наблюдения, сроки наблю­дения, а также подготовительные работы к наблюдению, в том числе порядок комплектования и обучения кадров, необходимых для проведения наблюдения, порядок его проведения, приема и сдачи материалов, получения и представления предварительных и окончательных итогов и др. При организации статистического наблюдения обязательно должен быть решен вопрос о времени проведения наблюдения, включая выбор сезона наблюдения, ус­тановление срока (периода) и критического момента наблюдения.

Сезон (время года) для наблюдения следует выбрать такой, в котором изучаемый объект пребывает в обычном для него состо­янии. Например, перепись населения в нашей стране чаще всего проводится зимой, так как наблюдается наименьшее передвиже­ние населения.

Под периодом (сроком) проведения наблюдения понимается время начала и окончания сбора сведений.

Время наблюдения - это время, к которому относятся данные собранной информации. Для предупреждения неполного учета или повторного счета для всех единиц статистической совокупности ус­танавливается единое время регистрации изучаемых показателей.

Критической называют дату, по состоянию на которую сооб­щаются сведения. При переписях обычно устанавливаются вре­мя начала (дата, а иногда и час) и время окончания регистрации наблюдения фактов. Например, Всесоюзная перепись населения 1989 г. проводилась в течение 8 дней, с 12 по 19 января.

Критическим моментом наблюдения выбирают полночь, мо­мент окончания одних суток и начала других. Так, критическим моментом Всесоюзной переписи населения в 1989 г. было 12 ч ночи с 12 января на 13 января. Все сведения о каждом жителе страны фиксировались такими, какими они были по состоянию на данный момент. Умершие после 12 ч ночи вносились в пере­писные листы, а родившиеся после 12 ч ночи учету не подлежали и в переписные листы не записывались.

4.

Материалы, собранные в результате статистического наблюдения, подвергаются всесторонней проверке и контролю. Как показывает практика, даже при четко организованном статистическом наблюдении встречаются погрешности, ошибки, требующие исправления. На современном этапе контроль данных в условиях сплошной информатизации приобретает особое значение. Предусматриваются различные методы проверки получаемых данных. Это, прежде всего, счетный (арифметический) и логический контроль.

Счетный (арифметический) контроль сводится к проверке общих и групповых цифровых итогов и их сопоставлению; задача его - обнаружить и исправить неверные итоги числовых показателей.

Логический контроль проводится путем сопоставления полученных данных с другими известными признаками, показателями. Возможно сопоставление за прошлый период по одной и той же единице, или за один и тот же период с данными по другой единице наблюдения. В результате контроля выявляются неправдоподобные случаи, т.е. логический контроль выявляет возможность ошибки.

Ошибки наблюдения по источнику происхождения можно подразделить на следующие:

· преднамеренные (злостные),

· непреднамеренные.

Непреднамеренные ошибки в свою очередь подразделяются наследующие:

· случайные,

· систематические,

· репрезентативности (представительности).

В соответствии с этими особенностями методы контроля данных могут быть разными.

Преднамеренные ошибки завышают или занижают конкретные значения признака, показателя. Они могут грубо искажать действительное положение. Поэтому преднамеренные ошибки требуют сплошного контроля.

Случайные ошибки чаще связаны с невнимательностью регистратора, небрежностью в заполнении документации, неточностью измерительных приборов и т.п. При достаточно большом числе зарегистрированных явлений они могут нейтрализовать друг друга. И все же подчеркнем, что одной из задач наблюдения является исключение таких ошибок. В целях контроля программа может предусматривать использование опознавательных признаков. Они образуют адресную часть и содержат, например, фамилию, имя и отчество, адрес и т.п. В случае обнаружения ошибки эти признаки позволяют обратиться к источнику информации и исправить ошибку.

Возможно включение в программу контрольных вопросов. Они позволяют, например, уточнить возраст по году рождения или выполнить логический контроль данных.

Непреднамеренные систематические ошибки возникают в самых различных ситуациях, например, при округлении признака в большую или меньшую сторону. Или при изучении бюджетов семей выясняется, что некоторые виды расходов забываются. Такие ошибки требуют корректировки в соответствии с особенностями явлений и процессов. Ошибки представительности, или репрезентативности, свойственны только выборочному наблюдению. Они показывают, в какой степени выборочная совокупность представляет (репрезентует) генеральную совокупность. Эти ошибки возникают вследствие того, что наблюдению подвергается лишь часть единиц изучаемой совокупности, и сведения, полученные в результате этого, не могут абсолютно точно отобразить свойства всей массы явлений совокупности.

Достоверность статистических данных обеспечивается различными способами. К ним относятся: рациональная разработка программы наблюдения и инструкций, разъясняющих содержание показателей: систематический контроль и проверка постановки учета и отчетности на всех предприятиях, в учреждениях и организациях; подбор и подготовка кадров и т.д.

Ряды распределения

Пример построения аналитической группировки

1.

Обработка статистических данных обычно начинается с построения группировок.

Группировка –распределение единиц совокупности на группы однородные в каком-то существенном отношении и характеристика выделенных групп с помощью статистических показателей.

Результаты группировки представляются в виде таблиц.

С помощью группировок решается несколько задач, основными из которых являются:

1) выделение типов социально-экономических явлений – с помощью типологической группировки (например: группировка предприятий по формам собственности, группировка населения по социальным группам и т.д.);

2) изучение структуры статистической совокупности - с помощью структурных группировок и рядов распределения (например: группировка по полу);

3) изучение взаимосвязи между признаками - с помощью аналитической группировки.

Группировка, в которой группы образованы по одному признаку, называется простой. Для характеристики явления бывает недостаточно разбить совокупность на группы по какому-либо одному признаку. В этом случае строят сложные (комбинационные) группировки.

Сложной называется группировка, в которой разделение совокупности на группы производится по двум и более признакам, взятым в сочетании (комбинации).

2.

1)Выбор группировочного признака (признаков) – выбор производится исходя из целей исследования.

2)Определение числа групп и величины интервала группировки.

Если группировка проводится по атрибутивному признаку, то обычно выделяют столько групп, сколько значений этого признака.

Если значений этого признака много, то пользуются классификацией (классификатор профессий).

Если группировка проводится по дискретному признаку и значений этого признака немного, то выделяют столько групп, сколько значений этого признака.

Если группировка проводится по непрерывному признаку или дискретному со многими значениями, то число групп можно определить по следующей формуле:

n = 1+3,322 lgN,

где N-число единиц совокупности.

Если признак непрерывный или дискретный со многими значениями, необходимо найти интервал группировки.

Интервалы бывают:

· равные, когда разность между максимальным и минимальным значениями в каждом из интервалов одинакова;

· неравные, когда, например, ширина интервала постепенно увеличивается, а верхний интервал часто не закрывается вовсе;

· открытые, когда имеется только либо верхняя, либо нижняя граница;

· закрытые, когда имеются и нижняя, и верхняя границы.

В случае равных интервалов величина интервала может быть определена как:

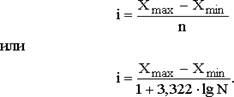
где i - величина интервала;

n – число групп;

Xmax, Xmin – максимальное и минимальное значения признака.

3) Подсчет численности единиц совокупности в каждой группе и по совокупности в целом.

4)Характеристика выделенных групп с помощью различных статистических показателей (Методика их расчета будет рассматриваться в процессе изучения).

5) Оформление результатов группировки в таблице.

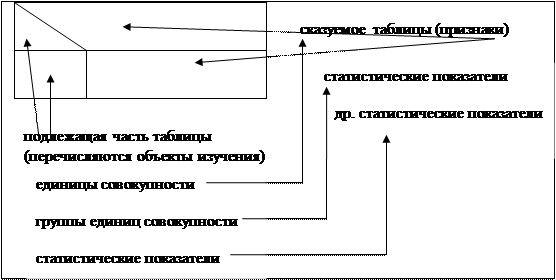
Рис. 2. Схема таблицы

Почти всегда признаки и статистические показатели имеют единицы измерения,которые должны быть указаны в таблице.

После таблицы обязательно должны быть сделаны выводы и разъяснения.

3.

Ряд распределения – это группировка, с помощью которой устанавливается распределение единиц совокупности по величине или значению некоторого признака.

Ряды, построенные по атрибутивному признаку, называются атрибутивными рядами распределения.

Ряды распределения, построенные по количественному признаку, называются вариационными рядами.

Примером атрибутивных рядов могут служить распределения населения по полу, занятости, национальности, профессии и т.д.

Примером вариационного ряда распределения может служить распределение населения по возрасту, рабочих – по стажу работы, заработной плате и т.д.

Вариационные ряды в зависимости от характера вариации подразделяются на дискретные и интервальные.

Вариационные ряды распределения состоят их двух элементов вариантов и частот.

Вариантами называются числовые значения количественного признака в ряду распределения, они могут быть положительными и отрицательными, абсолютными и относительными.

Частоты – это численности отдельных вариантов или каждой группы вариационного ряда. Сумма всех частот называется объемом совокупности и определяет число элементов всей совокупности.

Может быть рассчитана относительная частота, или частость, которая покажет долю каждой группы в совокупности.

Рассмотрим пример дискретного ряда распределения.

Таблица 1. Распределение рабочих цеха по

Тарифным разрядам

Тарифный разряд	Число рабочих	В % к итогу	Накопленная частота
		20,0 32,0 30,0 11,0 7,0
итого		100,0	----

1) Тарифный разряд – признак, по которому распределяют. 2,3,4,5,6 – варианты.

2) Число рабочих: 40, 64, 60, 22, 14 – частоты.

3) В % к итогу: 20,0; 32,0; 30,0; 11,0; 7,0 – частости.

Выводы: в этом цехе больше половины рабочих имеют 3 и 4 разряды, т.е. средний уровень квалификации.

Графически дискретный ряд распределения может быть представлен полигоном распределения.

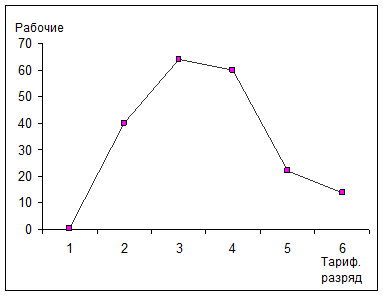
Рис. 3. Распределение рабочих цеха по тарифным разрядам

Пример. По следующим данным построить интервальный ряд распределения, выделив 4 группы предприятий с равными интервалами по величине основных средств.

Таблица 2. Стоимость основных средств и объем продукции

По предприятиям

Номер предприятия	Основные средства, млрд. руб	Объем продукции, млрд. руб.
	1,8 1,2 2,8 2,4 3,1 5,2 3,9 3,5 3,5 4,3 4,5 4,0	2,2 1,0 2,8 2,9 3,6 6,4 4,3 4,6 4,5 5,6 5,4 4,8

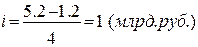
Таблица 3. Распределение предприятий

Рис. 4. Гистограмма распределения предприятий

Таблица 5. Зависимость объема продукции от основных средств.

Основные средства, млрд.руб.	Число предприятий	В среднем на одно предприятие
Основные средства, млрд. руб.	Объем продукции, млрд. руб
1,2-2,2 2,2-3,2 3,2-4,2 4,2-5,2		1,5 2,8 3,7 4,7	1,6 3,1 4,5 5,8
Итого		3,3	4,0

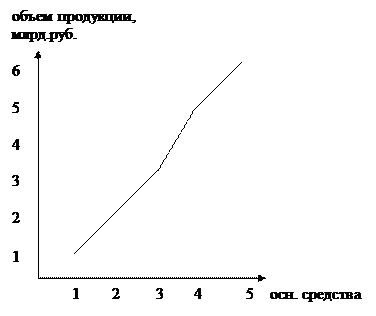Так как с увеличением основных средств происходит увеличение объемов продукции в среднем на 1 предприятие, то между этими двумя признаками прямая связь.

Рис.5. Зависимость объема продукции от основных средств.

Абсолютные величины.

Относительные величины.

1.

Изучая массовые общественные явления, статистика в своих выводах опирается на числовые данные, полученные в конкретных условиях места и времени. Результаты статистического наблюдения регистрируются, прежде всего, в форме первичных абсолютных величин.

Для характеристики совокупности в целом или ее отдельных частей рассчитывают обобщающие статистические показатели.

Абсолютная величина – это простейший статистический показатель характеризующий либо численность единиц совокупности (группы) либо сумму значений признака по группе.

Абсолютные величины являются результатом суммирования других величин. Иногда абсолютная величина является разностью двух других абсолютных величин (прибыль = выручка – себестоимость).

В статистике все абсолютные величины являются именованными, измеряются в конкретных единицах и, в отличие от математического понятия абсолютной величины, могут быть как положительными, так и отрицательными (убытки, убыль, потери и т.п.).

Рассмотрим виды единиц измерения абсолютных величин.

Натуральные единицы измерения могут быть простыми (тонны, штуки, метры, литры) и сложными, являющимися комбинацией нескольких разноименных величин (грузооборот железнодорожного транспорта выражается в тонно-километрах, производство электроэнергии – в киловатт-часах). Натуральные единицы измерения характеризуют либо физические свойства единиц совокупности, либо их численность.

В статистике применяют и абсолютные показатели, выраженные в условно-натуральных единицах измерения (например, различные виды топлива пересчитываются в условное топливо). Эти единицы измерения используются тогда, когда нужно определить суммарные объемы продукции, сырья, топлива для продуктов близких потребительскому назначению. В этом случае выбирают т.н. продукт-представитель и помощью коэффициентов пересчета переводят объемы всех других видов продукции в объем продукта-представителя. Продуктом-представителем выбирается продукт с наибольшим объемом производства или традиционный продукт.

Коэффициенты пересчета рассчитываются на основе определенной важной характеристики продукции (см. табл.6).

:

Таблица 6. Пересчет моющих веществ

в условное мыло 40% жирности

Виды моющих средств	Выпуск, тыс. т.	Содержание жира, %	Коэффициент пересчета	Выпуск условного мыла, тыс. т.
Мыло хозяйств. Мыло туалет. Порошок Паста моющая		40,0 70,0 20,0 50,0	1,0 1,75 0,5 1,25
Итого	--	--	--

Стоимостные единицы измерения используются, например, для выражения объема разнородной продукции в стоимостной (денежной) форме – рублях. При использовании стоимостных измерителей принимают во внимание изменения цен с течением времени. Этот недостаток стоимостных измерителей преодолевают применением "неизменных" или "сопоставимых" цен одного и того же периода. Кроме того стоимостные единицы используются для измерения всех макропоказателей.

В трудовых единицах измерения (человеко-днях, человеко-часах) учитываются общие затраты труда на предприятии, трудоемкость отдельных операций.

Человеко - дни = Численность работников (рабочих) х Время в днях

Человеко – часы = Численность рабочих х Время в часах

2.

Относительная величина в статистике – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин. Так как многие абсолютные величины взаимосвязаны, то и относительные величины одного типа в ряде случаев могут определяться через относительные величины другого типа. Могут рассчитываться относительные величины и путем сопоставления средних величин и других статистических показателей.

Основное условие правильного расчета относительной величины – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Таким образом, по способу получения относительные показатели – всегда величины производные, определяемые в форме коэффициентов, процентов, промилле, продецимилле и т.п. Однако нужно помнить, что этим безразмерным по форме показателям может быть, в сущности, приписана конкретная, и иногда довольно сложная, единица измерения. Так, например, относительные показатели естественного движения населения, такие как коэффициенты рождаемости или смертности, исчисляемые в промилле (‰), показывают число родившихся или умерших за год в расчете на 1 000 человек среднегодовой численности; относительная величина эффективности использования рабочего времени – это количество продукции в расчете на один отработанный человеко-час и т.д.

Относительная величина представляет собой дробь. Знаменатель дроби называется базой сравнения.

Если при расчете относительной величины база сравнения принимается за 1, то относительная величина выражается коэффициентом.

Если при расчете относительной величины база сравнения принимается за 100, то относительная величина в процентах.

В экономических расчетах чаще всего используются 4 относительные величины;

1) относительная величина структуры:

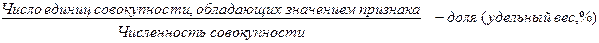
Используется для характеристики структуры совокупности

2) относительная величина планового задания:

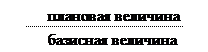
Пример. На предприятии планируют поднять заработную плату в этом квартале на 10%

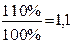
3) относительная величина выполнения плана:

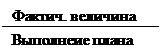
План по росту заработной платы недовыполнен на 6%

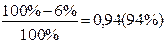
4) относительная величина динамики (темп роста) характеризует изменение во времени:

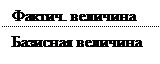
Взаимосвязь: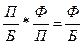

Относительная величина динамики равна произведению относительной величины планового задания и относительной величины выполнения плана.

Пример. Как фактически изменилась заработная плата на этом предприятии:

1,1*0,94=1,034 или 103,4%,

т.е. заработная плата увеличилась на 3,4% по сравнению с предыдущим кварталом.

Для более глубокого анализа можно рассчитать следующие относительные величины:

Относительные величины координации - характеризуют отношение частей данной совокупности к одной из них, принятой за базу сравнения. ОВК показывают, во сколько раз одна часть совокупности больше другой либо сколько единиц одной части приходится на 1, 10, 100, 1000, ... единиц другой части. Относительные величины координации могут рассчитываться и по абсолютным показателям, и по показателям структуры.

Пример. В районе проживает 284,5 тыс. чел. Населения, из них в городе – 188,9 тыс. чел. в селе – 95,6 тыс. чел. Относительная величина координации: 95,6 : 188,9 х 100 = 50 чел. сельского населения на 100 чел. городского населения.

Относительные величины сравнения или наглядности - характеризуют сравнительные размеры одноименных абсолютных величин, относящихся к одному и тому же периоду либо моменту времени, но к различным объектам или территориям то есть различным совокупностям. Посредством этих показателей сопоставляются мощности различных видов оборудования, производительность труда отдельных рабочих, производство продукции данного вида разными предприятиями, районами, странами, зарплата в государственном и частном секторах.

Относительные величины интенсивности - характеризуют степень распространения или развития данного явления в той или иной совокупности.. Представляют собой отношение абсолютного уровня одного показателя, характеризующего совокупность, к другому абсолютному показателю, также характеризующему совокупность. Так, при изучении демографических процессов рассчитываются показатели рождаемости, смертности, естественного прироста и т.д. как отношение числа родившихся (умерших) или величины прироста населения за год к среднегодовой численности населения данной территории в расчете на 1000 чел. Если получаемые значения очень малы, то делают расчет на 10 000 человек.

Важнейшими относительными величинами интенсивности являются показатели экономического развития страны, которые используются в международных сопоставлениях. Это такие показатели, как производство ВВП на душу населения, жилплощадь на душу населения, производство электроэнергии на душу населения и т.п.

В отличие от других относительных величинах, которые выражаются коэффициентами или %, величины интенсивности являются именованными числами (производство электроэнергии на душу населения в квт.-час.)

Правило сложения дисперсий.

Таблица 7. Виды степенных средних

Вид степенной средней	Показатель степени (m)	Формула расчета
Простая	Взвешенная
Гармоническая	-1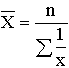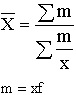
Геометрическая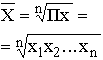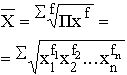
Арифметическая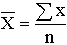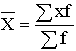
Квадратическая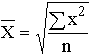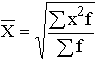
Кубическая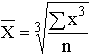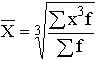

Формулы средневзвешенные могут использоваться для расчета общей по совокупности средней на основе групповых средних.

Пример. Рассчитать среднюю заработную плату по двум бригадам.

Таблица 8. Оплата труда по бригадам

№ бригады	Средняя заработная плата, тыс. руб.	Численность бригады, чел.
Итого	4987,5

Таблица 9. Оплата труда по бригадам

№ бригады	Средняя заработная плата, тыс. руб	Фонд заработной платы, тыс.руб.
Итого	4987,5

В обеих задачах определяющей функцией является ФЗП.

Прежде, чем выбрать формулу для расчетов средней величины ,нужно словами записать логическую сущность усредняемого признака.

Средняя заработная плата = Фонд заработной платы / численность работников

Средняя урожайность = Валовой сбор / Посевная площадь

Средняя производительность труда = Объем продукции / Численность (Время)

Правило:Если в представленной информации есть данные о числителелогической формулы, то есть об определяющей функции, то для расчета средней величины используется средняя гармоническая. Если представлены данные о знаменателе логической формулы, то для расчета средней величины используется средняя арифметическая.

Пример. В течение 8-часового рабочего дня пять рабочих производили одинаковые детали. Их затраты времени на одну деталь, мин.: 20, 16, 20, 15, 24. Определить средние затраты времени на одну деталь.

Средние затраты времени на одну деталь определяются путем деления суммарного времени на число деталей.

480 +480+480+480+480

480:20+480:16+480:20+480:15+480:24

(2400:130=18,46 мин.)

Это - правильный расчет, а неправильно, если сложить все затраты времени на одну деталь и разделить на пять (19 мин.). При таком расчете искажается объем производства деталей (2400:19=126, а не 130, как фактически).

2.

1.Средняя арифметическая постоянной величины равна этой постоянной:

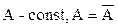
2.Алгебраическая сумма линейных отклонений варианты от средней арифметической равна 0 (нулевое свойство):

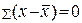– для несгруппированных данных,

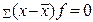– для сгруппированных данных;

3.Сумма квадратов отклонений варианты от средней арифметической есть число минимальное:

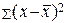– min(для несгруппированных данных),

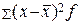– min(для сгруппированных данных);

Эти три свойства определяют сущность средней арифметической. Следующие свойства – расчетные.

4.Если каждую варианту Х уменьшить или увеличить на определенное число, то средняя величина уменьшается или увеличивается на это число.

5.Если каждую варианту Х уменьшить или увеличить в одно и то же число раз, то средняя величина уменьшается или увеличивается в это число раз.

6.Если каждую частоту f уменьшить или увеличить в одно и то же число раз, то средняя величина не изменится.

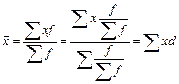
Доля каждой варианты (d) определяется путем деления каждой частоты на сумму всех частот.

Таким образом средняя величина зависит от варианты Х и от структуры совокупности, которая характеризуется долями d.

7.Средняя суммы равна сумме средних:

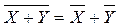
3.

Ряд распределения имеет 3 центра:

1) средняя арифметическая;

2) мода;

3) медиана.

Рассчитаем среднюю арифметическую для дискретного ряда распределения, представленного в таблице 1:

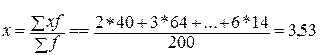
При расчете средней величины по интервальному ряду распределения в качестве варианты Х берется середина интервала. Если интервал открытый, то при расчете средней величины его условно закрывают, принимая равным соседнему закрытому интервалу.

Рассчитаем среднюю величину основных средств по таблице 3:

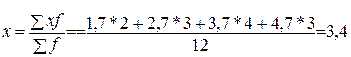млрд .руб.

В таблице 5 была рассчитана эта же величина, и она получилась равной 3,3 млрд. руб. (Объяснить различия)

Мода – наиболее часто встречающаяся варианта.

Определим моду тарифного разряда по таблице 1:

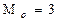
Для интервальных рядов распределения сначала находится модальный интервал, то есть интервал с наибольшей частотой внутри этого интервала, затем мода находится по формуле:

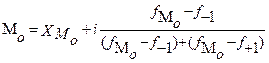
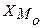- нижняя граница модального интервала;

i- величина модального интервала;

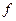- частота модального интервала;

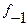- частота интервала предшествующего модальному интервалу;

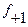-- частота интервала следующего за модальным интервалом.

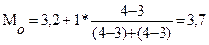млрд. руб.

Медиана - варианта, стоящая в середине ряда распределения.

Номер медианы:

№ Ме= 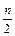- если число единиц в совокупности четное;

№ Ме= 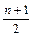- если число единиц в совокупности нечетное.

Найдем медиану тарифного разряда по таблице 1:

№ Ме=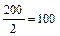

Ме=3

Следовательно, половина рабочих цеха имеет разряд не выше 3-го.

Прежде чем найти медиану для интервального ряда распределения, ищут интервал, в который входит срединная варианта, затем внутри этого интервала определяют медиану по формуле:

,

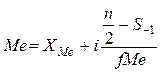где 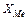- нижняя граница медианного интервала;

i- величина медианного интервала;

n- число единиц совокупности;

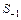- накопленная частота интервала предшествующего медианному;

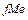- частота медианного интервала

Найдем медиану основных средств по таблице 3:

№ Ме=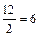

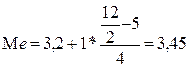млрд .руб.,

То есть половина предприятий имеет основные средства не выше, чем 3,45 млрд. руб.

4.

Ряды распределения, имеющие одинаковую среднюю величину, могут существенно отличаться по степени колеблемости изучаемого признака. (Пример. Средний возраст студентов в группе и бабушки с детьми).

Для характеристики совокупности, особенно, в том случае, если значение признака существенно колеблется, дополнительно к расчету средней величины определяют ряд показателей вариации.

Для измерения вариации используют абсолютные и относительные показатели.

1. Размах вариации: R = X _max – X _min – диапазон изменения признака.

2. Среднее линейное отклонение – показывает среднее отклонение варианты от средней величины:

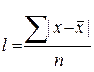- для несгруппированных данных;

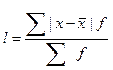- для сгруппированных данных;

3. Среднее квадратическое отклонение - показывает среднее отклонение вариант от средней величины:

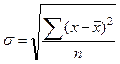- для не сгруппированных данных;

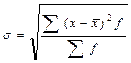- для сгруппированных данных;

Все 3 показателя имеют те же единицы измерения, что и признак.

4. Дисперсия – квадрат среднего квадратического отклонения:

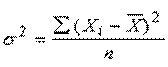
или