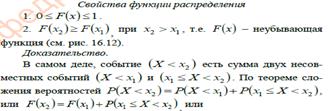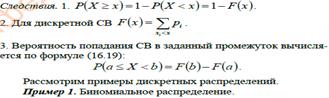Зависимые и независимые события.

Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.

Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.

События называются зависимыми, если одно из них влияет на вероятность появления другого.

26.

27. Приближенные формулы для схемы Бернулли

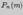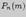Нахождение вероятностей по формуле Бернулли при достаточно больших значениях сопряжено с большим числом вычислений. Это обстоятельство было отмечено в ряде работ математиков начала XVIII века, посвященных демографическим проблемам. Возникла необходимость в асимптотических формулах как для , так и для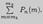

Из локальной предельной теоремы Муавра-Лапласа следует приближенная формула

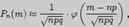
где 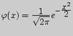и таблица значений функции приведена в приложении 1.

Из интегральной теоремы Муавра-Лапласа следует приближенная формула для вычисления числа "успехов" от 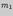до

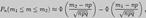
где 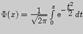- функция Лапласа, таблица значений которой приведена в приложении 2.

Из предельной теоремы Пуассона следует приближенная формула

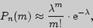
причем 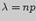, а таблица значений функции 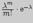имеется в приложении 3.

Формулы Бернулли, Муавра-Лапласа и Пуассона применяются в тех случаях, когда рассматриваются испытания, удовлетворяющие схеме Бернулли. При этом важно правильно выбрать соответствующую формулу.

28 Определение случ велечины закон распр функц и св-ва

Свойство 1. Функция распределения есть неотрицательная функция, заключенная между нулем и единицей:

.

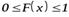Справедливость этого свойства вытекает из того, что функция распределения 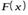определена как вероятность случайного события, состоящего в том, что .

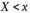Свойство 2. Вероятность попадания случайной величины в интервал 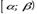равна разности значений функции распределения на концах этого интервала, т. е.

.

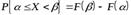Отсюда следует, что вероятность любого отдельного значения непрерывной случайной величины равна нулю.

Свойство 3. Функция распределения случайной величины есть неубывающая функция, т. е. при .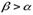

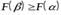Свойство 4. На минус бесконечности функция распределения рана нулю, а на плюс бесконечности функция распределения рана единице, т. е. , .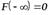

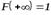Законом распределения случайной величины называется всякое соответствие между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения. Две случайные величины называются независимыми, если закон распределения одной из них не зависит то того, какие возможные значения приняла другая величина. В противном случае случайные величины называются зависимыми. Несколько случайных величин называются взаимно независимыми, если законы распределения любого числа из них не зависит от того, какие возможные значения приняли остальные величины.

Закон распределения случайной величины может быть задан в виде таблицы, в виде функции распределения, в виде плотности распределения. Таблица, содержащая возможные значения случайной величины и соответствующие вероятности, является простейшей формой задания закона распределения случайной величины:

29.

Дискретными случайными величинами называются случайные величины, принимающие только отдаленные друг от друга значения, которые можно заранее перечислить.