Понятие о системе линейно-угловых ходов

Совокупность линейно-угловых ходов, имеющих общие точки, называют системой ходов; узловой точкой называется точка, в которой сходятся не менее трех ходов. Как и для отдельного линейно - углового хода, для системы ходов применяют строгую и упрощенную обработку измерений; упрощенную обработку рассмотрим на примере системы из трех линейно-угловых ходов с одной узловой точкой (рис.2.23). Каждый ход опирается на исходный пункт с известными координатами; на каждом исходном пункте имеется направление с известным дирекционным углом.

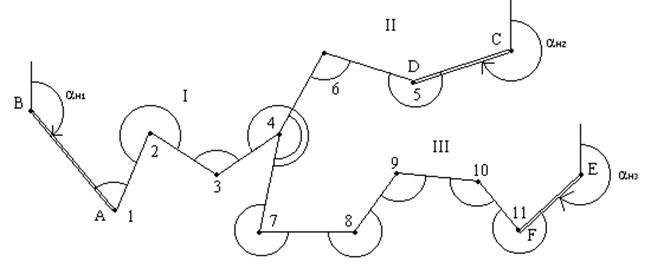
Рис.2.23. Система линейно-угловых ходов с одной узловой точкой.

Одну сторону какого-либо хода, проходящую через узловую точку, принимают за узловое направление (например, сторону 4 - 7) и вычисляют ее дирекционный угол по каждому ходу в отдельности, начиная от начального дирекционного угла в ходе. Получают три значения дирекционного угла узлового направления:

α1 - из первого хода,
α2 - из второго хода,
α3 - из третьего хода,

и вычисляют средневесовое значение из трех, причем за вес отдельного значения принимают число 1 / ni, где ni - количество углов в ходе от исходного направления до узлового направления (на рис.2.20 n1 = 4, n2 = 3, n3 = 5):

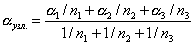(2.94)

Считая узловое направление исходным, то-есть, имеющим известный дирекционный угол, вычисляют угловые невязки в каждом ходе по отдельности и вводят поправки в измеренные углы. По исправленным углам вычисляют дирекционные углы всех сторон каждого хода и затем - приращения координат по всем сторонам ходов.

По приращениям координат вычисляют координаты узловой точки по каждому ходу в отдельности и получают три значения координаты X и три значения координаты Y узловой точки.

Средне-весовые значения координат подсчитывают по формулам:

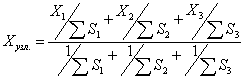(2.95),

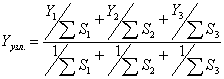(2.96)

Считая узловую точку исходным пунктом с известными координатами, вычисляют координатные невязки для каждого хода в отдельности и вводят поправки в приращения координат по сторонам ходов. По исправленным приращениям координат вычисляют координаты пунктов всех ходов.

Если сказать кратко, то упрощенная обработка системы линейно - угловых ходов с одной узловой точкой состоит из двух этапов: получение дирекционного угла узлового направления и координат узловой точки и обработка каждого хода в отдельности.

Понятие о триангуляции

Триангуляция представляет собой группу примыкающих один к другому треугольников, в которых измеряют все три угла; два или более пунктов имеют известные координаты, координаты остальных пунктов подлежат определению. Группа треугольников образует либо сплошную сеть, либо цепочку треугольников.

Координаты пунктов триангуляции как правило вычисляют на ЭВМ по программам, реализующим алгоритмы строгого уравнивания по МНК. На стадии предварительной обработки триангуляции последовательно решают треугольники один за другим. В нашем курсе геодезии мы рассмотрим решение лишь одного треугольника.

В первом треугольнике ABP (рис.2.24) известны координаты двух вершин (A и B) и его решение выполняют в следующем порядке:

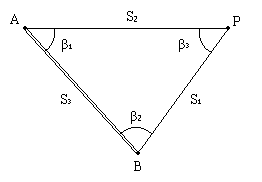
Рис.2.24. Единичный треугольник триангуляции

Вычисляют сумму измеренных углов ,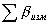

Принимая во внимание, что в треугольнике Σβ = 180о, вычисляют угловую невязку:

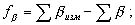
Поскольку

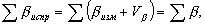
то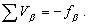

Это уравнение содержит три неизвестных поправки β и решить его можно лишь при наличии двух дополнительных условий.

Эти условия имеют вид:

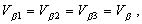
откуда следует, что

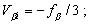
Вычисляют исправленные значения углов:

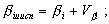
Решают обратную задачу между пунктами A и B вычисляют дирекционный угол αAB и длину S3 стороны AB.

По теореме синусов находят длины сторон AP и BP:

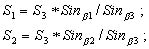
Вычисляют дирекционные углы сторон AP и BP:

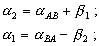
Решают прямую геодезическую задачу из пункта A на пункт P и для контроля - из пункта B на пункт P; при этом оба решения должны совпасть.

В сплошных сетях триангуляции кроме углов в треугольниках измеряют длины отдельных сторон треугольников и дирекционные углы некоторых направлений; эти измерения выполняются с большей точностью и играют роль дополнительных исходных данных. При уравнивании сплошных сетей триангуляции в них могут возникнуть следующие условия:

условия фигуры,

условия суммы углов,

условия горизонта,

полюсные условия,

базисные условия,

условия дирекционных углов,

координатные условия.

Формула для подсчета количества условий в произвольной сети триангуляции имеет вид:

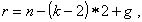
где n - общее количество измеренных углов в треугольниках,
k - число пунктов в сети,
g - количество избыточных исходных данных.

Понятие о трилатерации

Трилатерация представляет собой сплошную сеть примыкающих один к другому треугольников, в которых измеряют длины всех сторон; два пункта, как минимум, должны иметь известные координаты (рис.2.25).

Решение первого треугольника трилатерации, в котором известны координаты двух пунктов и измерены две стороны, можно выполнить по формулам линейной засечки, причем нужно указывать справа или слева от опорной линии AB располагается пункт 1. Во втором треугольнике также оказываются известными координаты двух пунктов и длины двух сторон; его решение тоже выполняется по формулам линейной засечки и так далее.

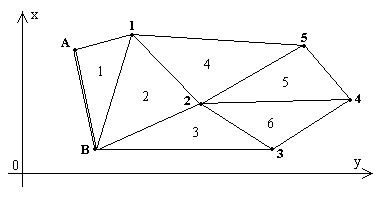
Рис.2.25. Схема сплошной сети трилатерации

Можно поступить и по-другому: сначала вычислить углы первого треугольника по теореме косинусов, затем, используя эти углы и дирекционный угол стороны AB, вычислить дирекционные углы сторон A1 и B1 и решить прямую геодезическую задачу от пункта A на пункт 1 и от пункта B на пункт 1.

Таким образом, в каждом отдельном треугольнике "чистой" трилатерации нет избыточных измерений и нет возможности выполнить контроль измерений, уравнивание и оценку точности; на практике кроме сторон треугольников приходится измерять некоторые дополнительные элементы и строить сеть так, чтобы в ней возникали геометрические условия.

Уравнивание сплошных сетей трилатерации выполняется на ЭВМ по программам, в которых реализованы алгоритмы МНК.