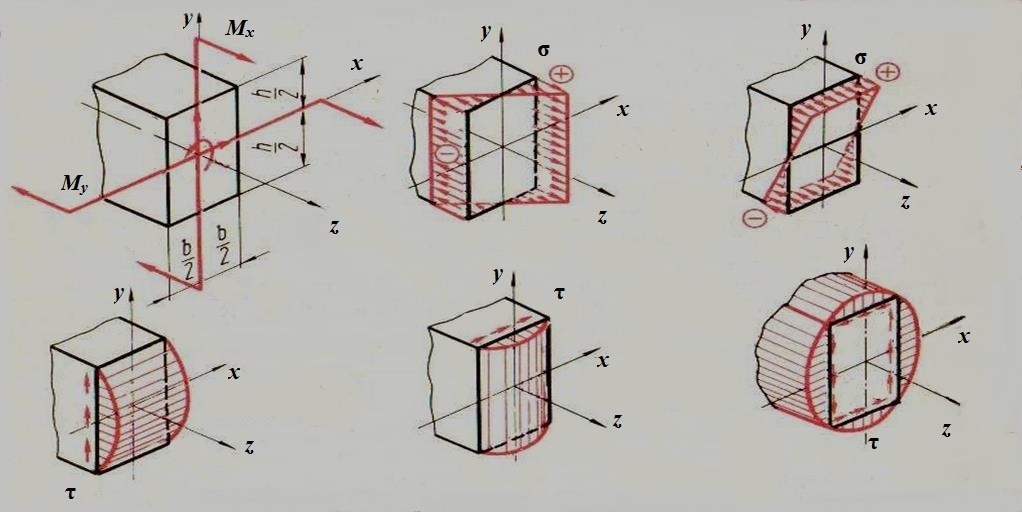
Чтобы не связывать себя формальными правилами знаков, слагаемые будем определять по модулю, а знаки ставить по смыслу.

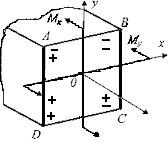
Например, верхний ряд знаков «+» и «—» соответствует напряжениям от М_x , а нижний ряд — от M_y

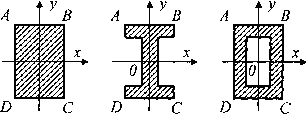В случае поперечных сечений (прямоугольник сплошной и полый, двутавр) имеющих две оси симметрии и выступающие угловые точки с равными по модулю и максимальными одноименными координатами

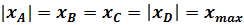
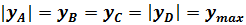
Напряжения в точках будут равны

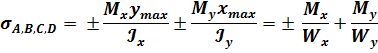
и напряжения в точках A,B,C,D будут равны:

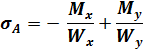
Точка А от М_xверхняя сила сжимает волокна, а нижняя растягивает, ставим знак минус, от M_yлевая сила растягивает волокна, а правая сжимает ставим знак плюс .

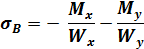
Точка В от М_xверхняя сила сжимает волокна, а нижняя растягивает, ставим знак минус,от M_yлевая сила сжимает волокна, а правая растягивает ставим знак минус.

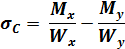
Точка C от М_xнижняя сила растягивает волокна, а верхняя сжимает, ставим знак плюс, от M_yлевая сила растягивает волокна, а правая сжимает ставим знак минус.

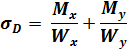
Точка D от М_x нижняя сила растягивает волокна, а верхняя сжимает, ставим знак плюс, от M_y левая сила растягивает волокна, а правая сжимает ставим знак плюс.

Рассмотрим распределение напряжений по поперечному сечению бруса.

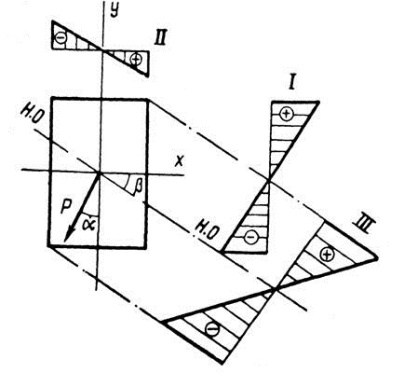Эпюра I показывает распределение напряжений от силы F_у (соответствующих моменту Мх), эпюра II – напряжений от силы Fx (соответствующих моменту My, ) аэпюра III суммарных напряжений

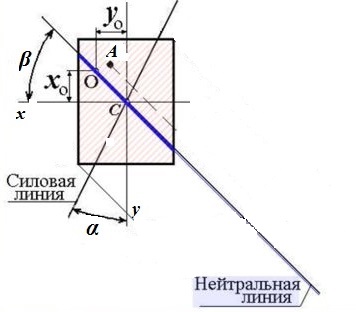
По эпюрам I и II легко установить в какую строрну от оси х должен быть отложен угол β, нейтральная ось должна пройти через те четверти (квадранты) сечения, в которых знаки составляющих напряжений различны. В рассматириваемом случае через 2 и 4 четверти.

Для построения эпюры суммарных напряжений надо предварительно найти положение нулевой нейтральной линии.

Условие прочности при косом изгибе..

Условие прочности для балок из пластичного материала для сечений типа прямоугольник, двутавр, швеллер запишется в виде:

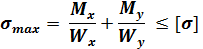
Или

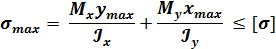
Касательные напряжения от поперечных сил, если нельзя воспользоваться формулой Журавского, допустимо не учитывать.

При проведении расчетов на прочность условие прочности составля­ется для опасной точки поперечного сечения, т.е. для точки, в которой нормальные напряжения достигают максимальных значений.

Самой нагруженной точкой в сечении произвольной формы является точка, наиболее удаленная от нейтральной линии, разделяющей растянутую и сжатую зоны сечения.

В связи с этим, большое значение приобретают вопросы, связанные с определением положения нейтральной линии.

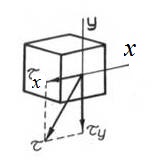Касательные напряжения возникают от поперечных сил.

Касательные напряжения от поперечной силы Fy

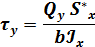
Касательные напряжения от поперечной силы Fx

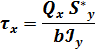
Полные напряжения τ при косом изгибе найдем путем геометрического суммирования составляющих:

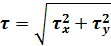
5. Положение нейтральной оси при косом изгибе.

Нулевой или нейтральной линией называется геометрическое место точек поперечного сечения, в которых нормальные напряжения равны нулю.