Векторные поля в трёхмерном пространстве
Если 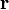 — радиус-вектор, который в заданной системе координат имеет вид
— радиус-вектор, который в заданной системе координат имеет вид 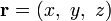 , то векторное поле описывается вектор-функцией вида:
, то векторное поле описывается вектор-функцией вида:
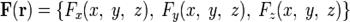
Билет№38. Формула Гаусса-Остроградского. Дивергенция векторного поля.
Формула Гаусса-Остроградского.






 Зададим в пространстве замкнутую трехмерную область V, ограниченную поверхностью S и проектирующуюся на плоскость Оху в правильную область D.
Зададим в пространстве замкнутую трехмерную область V, ограниченную поверхностью S и проектирующуюся на плоскость Оху в правильную область D.
z
S2 (z=f2(x,y))
S3
V
S1 (z=f1(x,y))
O y
x D
Рис. 1.
Будем считать, что поверхность S можно разбить на три части: S1, заданную уравнением z = f1(x, y), S2 ( z = f2 (x, y) ) и S3 – цилиндрическую поверхность с образующей, параллель-ной оси Oz (рис.1).
Зададим в каждой точке области V и поверхности S непрерывные функции P(x, y, z), Q(x, y, z) и R(x, y, z) и вычислим интеграл
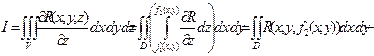
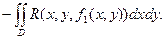
Зададим ориентацию поверхности S, выбрав направление внешней нормали, тогда на S1
cos(n, z) < 0, на S2 cos(n, z) > 0, a на S3 cos(n, z) = 0. Двойные интегралы, стоящие в правой части предыдущего равенства, равны соответствующим поверхностным интегралам:
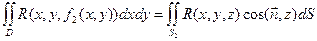 ,
,
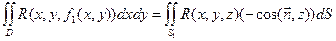 .
.
(Знак «-» во втором интеграле появляется за счет того, элементы площади поверхности S1 и области D связаны соотношением dxdy = ΔS(-cos(n, z)) ). Следовательно, исходный интеграл можно представить в виде:
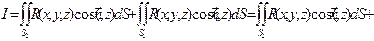
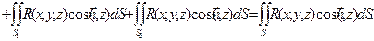
Окончательный результат можно записать так:
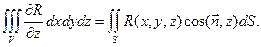
Таким же образом можно получить соотношения
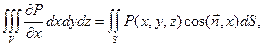
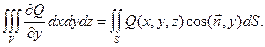
Складывая эти три равенства, получаем формулу Гаусса-Остроградского:
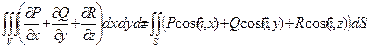 (15.1)
(15.1)
Воспользовавшись формулой 13.9, задающей связь между поверхностными интегралами 1-го и 2-го рода, можно записать формулу Гаусса-Остроградского в ином виде:

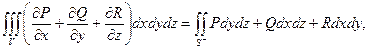 (15.2)
(15.2)
где запись «S+» означает, что интеграл, стоящий справа, вычисляется по внешней стороне поверхности S.
Дивергенция векторного поля.
Продолжим изучение характеристик векторных полей.
Определение 15.1. Дивергенциейвекторного поля A = {Ax, Ay, Az}, где Ax, Ay, Az – функции от x, y, z, называется
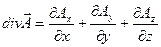 . (15.3)
. (15.3)
Замечание 1. Из определения видно, что дивергенция является скалярной функцией.
Замечание 2. Слово «дивергенция» означает «расходимость», так как дивергенция харак-теризует плотность источников данного векторного поля в рассматриваемой точке.
Рассмотрим формулу Гаусса-Остроградского с учетом определений потока и дивергенции векторного поля. Тогда в левой части формулы (15.1) стоит тройной интеграл по объему V от дивергенции векторного поля {P, Q, R}, а в правой – поток этого вектора через ограни-чивающую тело поверхность S:
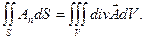 (15.4)
(15.4)
Докажем, что величина дивергенции в данной точке не зависит от выбора системы коор-динат. Рассмотрим некоторую точку М, которую окружает трехмерная область V, ограни-ченная поверхностью S. Разделим обе части формулы (15.4) на V и перейдем к пределу при стягивании тела V к точке М. Получим:
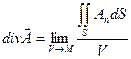 . (15.5)
. (15.5)
Это равенство можно считать инвариантным определением дивергенции, то есть определением, не зависящим от выбора координатной системы.
Билет№39. Формула Стокса. Ротор векторного поля.
Формула Стокса.
Рассмотрим поверхность S такую, что любая прямая, параллельная оси Оz, пересекает ее в одной точке. Обозначим границу поверхности λ и выберем в качестве положительного направления нормали такое, при котором она образует с положительным направлением оси Оz острый угол. Если уравнение поверхности имеет вид z = f(x, y), то направляющие косинусы нормали задаются формулами
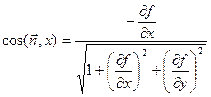 ,
, 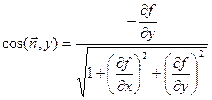 ,
,
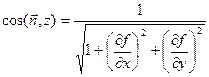 .
.
Рассмотрим некоторую трехмерную область V, в которой целиком лежит поверхность S, и зададим в этой области функцию P(x, y, z), непрерывную вместе с частными производны-ми первого порядка. Вычислим криволинейный интеграл 2-го рода по кривой λ:

 z
z 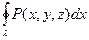 .
.
 n
n



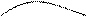







 σ
σ
λ
O y
 D
D
x L
Рис. 2.
Уравнение линии λ имеет вид z = f(x, y), где х, у – координаты точек линии L, являющейся проекцией λ на плоскость Оху (рис.2). Поэтому, используя формулу (10.8), получаем:
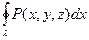 =
= 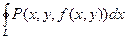 .
.
Обозначим P(x, y) = P(x, y, f(x, y)), Q(x, y) = 0 и применим к интегралу, стоящему в правой части предыдущего равенства, формулу Грина:
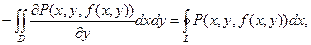
где область D ограничена линией L. Преобразуем левое подынтегральное выражение, используя формулу производной сложной функции:
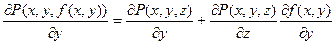
и подставим его в предыдущее равенство:
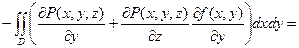
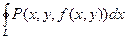 . Тогда
. Тогда
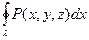 =
= 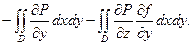 Теперь применим к интегралам, стоящим справа, формулу (13.7) и перейдем к поверхностным интегралам 1-го рода по поверхно-сти σ:
Теперь применим к интегралам, стоящим справа, формулу (13.7) и перейдем к поверхностным интегралам 1-го рода по поверхно-сти σ:
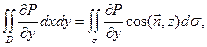
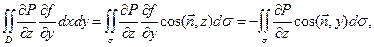
так как 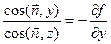 . Следовательно, окончательный результат преобразований выглядит так:
. Следовательно, окончательный результат преобразований выглядит так:
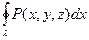 =
= 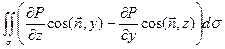 .
.
При этом направление обхода контура λ выбирается соответствующим положительному направлению нормали (рис.2).
Задавая в области V непрерывно дифференцируемые функции Q(x, y, z) и R(x, y, z), можно получить для них аналогичные соотношения:
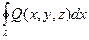 =
= 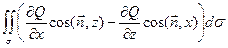 ,
,
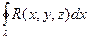 =
= 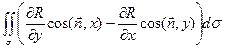 .
.
Складывая левые и правые части полученных равенств, получим формулу Стокса, уста-навливающую связь между поверхностным интегралом 1-го рода по поверхности σ и криволинейным интегралом 2-го рода по ограничивающему ее контуру λ с учетом ориен-тации поверхности:
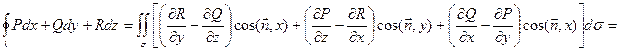
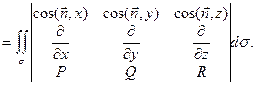 (15.6)
(15.6)
Последняя запись позволяет лучше запомнить подынтегральное выражение в правой части формулы Стокса, которое можно получить, раскрывая определитель по первой строке и учитывая, что во второй его строке стоят операторы частного дифференцирова-ния по соответствующим переменным, применяемые к функциям, стоящим в третьей строке.
Используя связь между поверхностными интегралами 1-го и 2-го рода (формула (13.9)), можно записать формулу Стокса в ином виде:
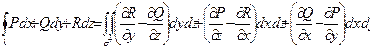 . (15.7)
. (15.7)
Ротор векторного поля.
Определение 15.2. Ротором или вектором вихрявекторного поля A = {Ax, Ay, Az}, где Ax, Ay, Az – функции от x, y, z, называется вектор, определяемый следующим образом:
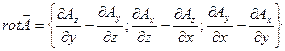 . (15.8)
. (15.8)
Замечание 1. Ротор характеризует завихренность поля А в данной точке, то есть наличие вращательных движений, так как его модуль равен удвоенной угловой скорости в этой точке.
Замечание 2. Формула Стокса в векторной формулировке имеет вид:

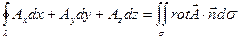 , (15.9)
, (15.9)
то есть циркуляция вектора по замкнутому контуру равна потоку ротора этого вектора через поверхность, натянутую на данный контур.
Замечание 3. Можно дать другое, инвариантное, определение ротора. Для этого рассмотрим произвольное направление п, исходящее из данной точки М, и окружим эту точку плоской площадкой σ, перпендикулярной к п и ограниченной контуром λ. Приме-няя формулу Стокса, получим:
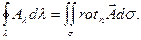
Разделив обе части этого равенства на σ и стягивая площадку σ к данной точке, найдем в пределе, что
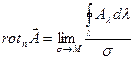 .
.
Тем самым можно определить проекцию ротора на любую ось, то есть вектор rot A не зависит от выбора координатной системы.
Билет №40. Сумма ряда. Сходимость. Ряд, составленный из членов бесконечно убывающей геометрической прогрессии. Основные свойства числовых рядов. Необходимый признак сходимости. Гармонический ряд.
Определение
Если дана бесконечная последовательность чисел 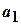 ,
, 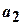 ,
, 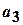 ,..., то выражение вида
,..., то выражение вида
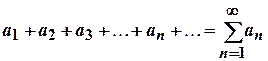 (1)
(1)
называется числовым рядом; числа 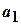 ,
, 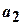 ,
, 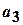 ,...– членами (элементами) ряда,
,...– членами (элементами) ряда, 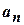 – общим членом ряда, если
– общим членом ряда, если 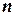 не зафиксировано.
не зафиксировано.
2 СХОДЯЩИЕСЯ И РАСХОДЯЩИЕСЯ РЯДЫ
Если дан ряд (1), то сумма первых n членов этого ряда называется 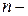 ой частичной суммой и обозначается через
ой частичной суммой и обозначается через 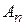 . Следовательно, суммы
. Следовательно, суммы
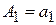 – 1-ая частичная сумма;
– 1-ая частичная сумма;
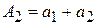 – 2-ая частичная сумма;
– 2-ая частичная сумма;
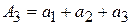 – 3-ая частичная сумма;
– 3-ая частичная сумма;
¼ – ……………………….
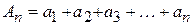 –
– 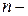 ая частичная сумма;
ая частичная сумма;
... – ……………………….
образуют последовательность частичных сумм 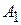 ,
, 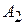 , ...,
, ..., 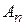 , ...
, ...
Определение
Ряд (1) называется сходящимся, если существует конечный предел последовательности частичных сумм, то есть 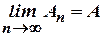 . При этом число
. При этом число 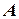 называется суммой ряда. Если для данного ряда последовательность частичных сумм
называется суммой ряда. Если для данного ряда последовательность частичных сумм 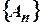 не имеет конечного предела при
не имеет конечного предела при 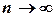 , то этот ряд называется расходящимся.
, то этот ряд называется расходящимся.
3 ОСНОВНЫЕ СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
1) Если ряд 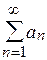 сходится, то сходится и ряд, полученный отбрасыванием из него любого конечного числа членов.
сходится, то сходится и ряд, полученный отбрасыванием из него любого конечного числа членов.
2) Пусть даны ряды 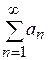 ,
, 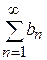 и
и 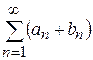 . Если оба ряда
. Если оба ряда 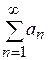 и
и 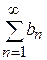 сходятся, а их суммы соответственно равны
сходятся, а их суммы соответственно равны 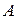 и
и 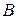 , то сходится и ряд
, то сходится и ряд 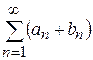 , причем его сумма равна
, причем его сумма равна 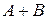 .
.
3) Если ряд 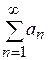 сходится и имеет сумму
сходится и имеет сумму 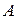 , то сходится и ряд
, то сходится и ряд 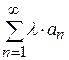 , причем его сумма равна числу
, причем его сумма равна числу 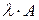 , где
, где 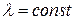 .
.
4) Если ряд 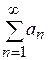 сходится, то сходится и любой ряд, полученный из него группировкой слагаемых, не изменяющей порядок расположения членов ряда, и суммы этих рядов одинаковы. К примеру, если
сходится, то сходится и любой ряд, полученный из него группировкой слагаемых, не изменяющей порядок расположения членов ряда, и суммы этих рядов одинаковы. К примеру, если 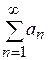 сходится и его сумма равна
сходится и его сумма равна 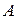 , то ряд
, то ряд
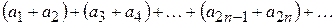
также сходится, и его сумма равна 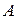 .
.
Эти свойства доказываются с помощью определения сходящихся рядов. Для примера докажем второе свойство.
Пусть 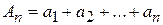 ,
, 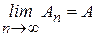 ,
,
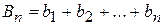 ,
, 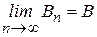 ,
,
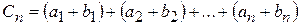 .
.
Очевидно, что при любом 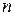
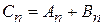 . Тогда
. Тогда 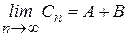 , что доказывает рассматриваемое свойство. ¨ (данный знак будет означать окончание доказательства теорем).
, что доказывает рассматриваемое свойство. ¨ (данный знак будет означать окончание доказательства теорем).
4 ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ
На практике часто не столь важно найти сумму ряда, как ответить на вопрос о сходимости ряда. Для этой цели используются признаки сходимости, основанные на свойствах общего члена ряда.
НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ РЯДА
ТЕОРЕМА 1
Если ряд 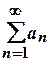 сходится, то его общий член
сходится, то его общий член 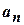 стремится к нулю при
стремится к нулю при 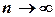 , т.е.
, т.е. 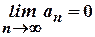 .
.
Кратко: если ряд сходится, то его общий член стремится к нулю.
Доказательство. Пусть ряд сходится и его сумма равна 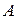 . Для любого
. Для любого 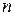 частичная сумма
частичная сумма
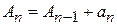
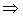
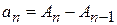 .
.
Тогда 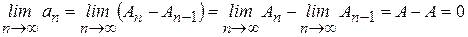 . ¨
. ¨
Из доказанного необходимого признака сходимости вытекает достаточный признак расходимости ряда: если при 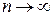 общий член ряда не стремится к нулю, то ряд расходится.
общий член ряда не стремится к нулю, то ряд расходится.
