Связь поверхностных интегралов первого и второго рода.

Учитывая, что проекции элемента поверхности S_i на координатные плоскости имеют вид S_icosγ, S_icosβ, S_icosα, из (13.5) получим:

, (13.9)

где векторное поле , а - векторное поле единичных нормалей заданно-го направления в каждой точке поверхности. Следовательно, поверхностный интеграл 2-го рода (13.5) равен поверхностному интегралу 1-го рода (13.9). Эта формула предо-ставляет еще одну возможность вычисления поверхностного интеграла 2-го рода. Заметим, что при смене стороны поверхности меняют знак направляющие косинусы нормали, и, соответственно, интеграл в правой части равенства (13.9), который сам по себе, как поверхностный интеграл 1-го рода, от выбора стороны поверхности не зависит.

Пример. Рассмотрим интеграл , где S – внешняя сторона верхней половины сферы x² + y² + z² = R². Так как радиус сферы, проведенный в любую ее точку, можно считать нормалью к сфере в этой точке, единичный вектор нормали можно задать в виде п = . Тогда, используя формулу (13.9), получаем, что требуется вычислить поверхностный интеграл 1-го рода

(Область D – круг с центром в начале координат радиуса R).

Билет 37 Векторное поле.Виды.

Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор.Когда исходное пространство — евклидово (конечномерное линейное пространство со скалярным произведением), понятие векторного поля становится наглядным, и тогда векторное поле интерпретируется как способ задания движений некоторой динамической системы: вектор в данной точке описывает направление и скорость движения изображающей точки по фазовой кривой.Векторное поле, заданное на евклидовом пространстве, соответствует полю направлений, где каждой точке пространства сопоставляется некоторая прямая, проходящая через данную точку.Точка пространства, в которой векторное поле равно нулю, называется особой точкой векторного поля. В этом случае направление движения не определено, и соответствующая фазовая кривая вырождается в точку.В более общем случае, когда исходное пространство является многообразием, векторное поле — это сечение касательного расслоения к данному многообразию.В физике термин векторное поле кроме общего значения, описанного выше, имеет специальное значение, в основном в отношении фундаментальных полей (см. ниже). Смысл этого употребления сводится к тому, что фундаментальные физические поля классифицируются по природе их потенциала, и один из таких типов — векторные поля (как электромагнитное или глюонное поля).

Виды векторных полей

1.Векторные поля на прямой. Любую вещественнозначную функцию вещественного переменного можно интерпретировать как одномерное векторное поле. 2.Векторные поля на плоскости. Если 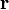— радиус-вектор, который в заданной системе координат имеет вид 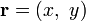, то векторное поле описывается вектор-функцией вида: