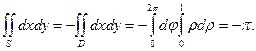Поверхностный интеграл второго рода.

Введем определение поверхностного интеграла 2-го рода по аналогии с соответ-ствующим криволинейным интегралом. Рассмотрим гладкую двустороннюю поверхность S, заданную уравнением z = z(x, y), в каждой точке которой определена функция f(M) = f(x, y, z), и выберем какую-либо из ее сторон (или, что то же самое, определенную ориентацию). Разобьем поверхность S на части S₁, S₂,…, S_п, выберем в каждой части S_i точку M_i(x_i, y_i, z_i), и умножим f(M_i) на площадь D_i проекции части S_i на плоскость Оху. При этом будем считать, проекция части верхней по отношению к плоскости Оху стороны рассматриваемой поверхности имеет знак «+», а нижней – знак «-». Составим сумму

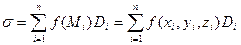. (13.2)

Определение 13.4. Если существует конечный предел суммы (13.2) при ρ→0, не зависящий от способа разбиения поверхности и выбора точек на ней, то он называет-ся поверхностным интегралом второго рода от функции f(M) по выбранной сто-роне поверхности S и обозначается

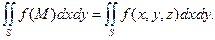(13.3)

Замечание. В этой символической записи не содержится указания на то, какая сторона поверхности выбрана, поэтому это требуется оговаривать отдельно.

Подобным образом можно проектировать части поверхности на координатные плос-кости Оxz и Оyz (при условии, что уравнение поверхности можно представить в виде y = y(x, z) или x = x(y, z) ). Получим два других поверхностных интеграла 2-го рода:

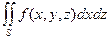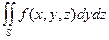и . (13.4)

Рассмотрев сумму интегралов вида (13.3) и (13.4) по одной и той же поверхности соответственно от функций P(x, y, z), Q(x, y, z), R(x, y, z), получим поверхностный интеграл второго рода общего вида:

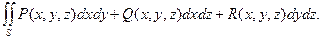(13.5)

Поверхностный интеграл 2-го рода представляет собой поток векторного поля 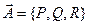через выбранную сторону поверхности S.

Отметим основное свойство поверхностного интеграла 2-го рода:

При замене рассматриваемой стороны поверхности на противоположную поверхностный интеграл 2-го рода меняет знак: 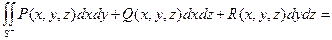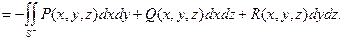(13.6) Справедливость этого утверждения следует из определения 13.4.

Вычисление поверхностного интеграла 2-го рода.

Если задать единичный вектор выбранной нормали к поверхности S в виде п = {cos α, cos β, cos γ}, где α, β, γ – углы, образованные нормалью с осями координат, то 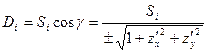(выбор знака зависит от направления нормали). Тогда из (13.2), (13.3) следует, что

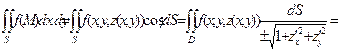
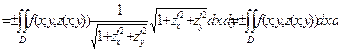. (13.7)

Здесь D – проекция поверхности S на плоскость Оху, а выражение для dS взято из формулы (12.5). Таким образом, вычисление поверхностного интеграла 2-го рода сводится к вычислению обычного двойного интеграла по области D от функции f, в которую вместо координаты z подставлено ее выражение из уравнения поверхности S. Обобщая эти рассуждения, получим, что

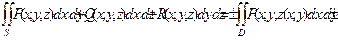
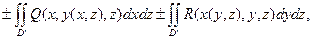(13.8)

где D΄ и D΄΄ - проекции поверхности S на соответствующие координатные плоскости.

Пример. Вычислить поверхностный интеграл 2-го рода 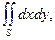где S – нижняя сторона части конуса 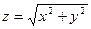при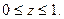

Применим формулу (13.7), учитывая, что выбрана нижняя сторона поверхности и что проекцией части конуса на плоскость Оху является круг 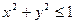: