Применение аппарата теории игр для анализа проблем микроэкономики

Введение понятия аппарата математической теории игр имеют прямое приложение для анализа проблем макроэкономики, в том числе для анализа рыночного равновесия как корпоративной игры многих лиц.

Рассмотрим пример экономической задачи, в которой имеются два субъекта:

Игрок 1 и Игрок 2, и два товара (блага) 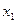и .

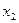Замечание. Число игроков и товаров может быть и большим, но в случае 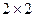все введение понятия имеют наглядную интерпретацию.

Каждый из игроков имеет свою функцию полезности заданную на наборе товаров: и ; предполагается, что эти функции непрерывны и монотонны по каждой из переменных и выпуклы. В начале игры в экономике имеется общее количество первого товара, и - второго товара.

Предположим, что начальное количество благ как-то распределено между игроками: первый Игрок обладает количеством первого товар и - второго товара, второй Игрок – количествами и - первого и второго товаров соответственно, так что и .

Возникают вопросы: могут ли игроки путем обмена, имеющегося у них товарами улучшить свое положение, т.е. увеличить значение функций полезност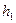и и 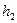по сравнению с начальными уравнениями и ; каковы свойства такого решения?

Для наглядности представления экономики с двумя игроками и двумя товарами, как правило, используется так называемый ящик Эджворта.

В ящике Эджворта, длина горизонтальной оси соответствует первому товару, численно равна общему количеству этого товара 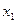, длина вертикальной оси – общему количеству товара 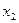. Выделенное пространство является множеством всех возможных распределений имеющихся товаров между двумя игроками.

Кривые безразличия 1 Игрока ----Кривые безразличия 2 Игрока

Нижний левый угол считается началом координат для первого Игрока, верхний правый угол – началом координат для второго Игрока. На выделенном пространстве представлены также два множества кривых безразличия (линий уровня функций выигрыша) принадлежащих каждому из игроков. При этом точка начального распределения товаров имеет координаты в системе отсчета первого Игрока (и соответственно - в системе отсчета второго Игрока).

Рассмотрим для начала проблему эффективного распределения товаров между игроками. При этом основное требование на начальном этапе анализа – это требование Парето- оптимальности.

Парето – оптимальным называют распределение, если положение ни одного из игроков нельзя улучшить, не ухудшая при этом положение его партнера.

Множество Парето – оптимального распределения может быть наглядно представлено на примере ящика Эджворта. В случае двух игроков Парето – оптимальное распределение может быть найдено с помощью фиксации уровня полезности одного из игроков (для примера Игрока 2) и поиска максимума функции полезности другого игрока.

Игрок 2

В терминах ящика Эджворта это означает, что необходимо найти такую точку на фиксированной прямой безразличия Игрока 2, в которой Игрок 1 получает максимум своей функции полезности. Очевидно, такой точкой является точка, где кривые касаются друг друга, так как в противном случае Игрок 1 продвигаясь вдоль фиксированной линии уровня Игрока 2 внутрь, увеличить значение своей функции полезности.

Математически это означает:

Максимум функции полезности Игрока 1 при фиксировании уровня полезности Игрока2 достигается в точке, в которой дифференциалы этой функции равны, т.е. в точке, где кривые безразличия имеют общую касательную.

Опираясь на этот факт, можно показать, что множество Парето - оптимальных распределений в ящике Эджворта будет множеством всех точек, в которых кривые безразличия Игрока 1 и Игрока 2 касаются друг друга. Множество Парето – оптимальности распределения в пространстве товаров называется контрактным множеством, поскольку игрокам в общем случае имеет смысл договариваться между собой именно на этом наборе эффективных распределений (сравнивается с множеством Парето – оптимальных стратегий в кооперативных играх).

Рассмотрим ситуацию, когда каждый игрок обладает начальным количеством каждого из товаров. Возникает вопрос: может ли это начальное распределение быть улучшено путем обмена товара между игрками?

Исследуем эту проблему с помощью ящика Эджворта.

Пусть - точка начального распределения товаров. Проведем через эту точку кривые безразличия для Игрока 1 и Игрока 2.

Если эти две кривые не касаются друг друга (т.е. если начальное распределение не является Парето – оптимальным), то своем пересечением они образуют область, двигаясь внутрь которой каждый из игроков может увеличить значение обеих функций полезности. При этом часть контрактного множества оказывается внутри области образованной кривыми безразличия.

Эти кривые, фиксируя начальные уровни полезности для каждого из игроков, аналогичны точке угрозы в теории кооперативных игр – поэтому их можно назвать линиями угрозы, а выделяемое ими множество – в микроэкономике называем переговорным множеством.

Для того чтобы переместиться в переговорное множестве Игрок 1 должен передать (продать) некоторое количество товара 2 имеющегося у Игрока 2.

Линии угрозы в данном случае означает, что за их пределами (т.е. ниже и левее исходной кривой безразличия для Игрока 1 и выше и правее кривой безразличия для Игрока 2) какому-либо из игроков становится не за чем чести переговоры – ему лучше (или, по крайней мере, не хуже) оставаться в ситуации начального распределения. Точка Нэша, соответствующая максимуму произведения приращений полезностей игроков по сравнению с начальной ситуацией, будет находиться внутри переговорного множества.

В результате проведенного анализа можно сделать вывод, что игроки могут улучшить свое первоначальное положение, обмениваясь товарами, и Игроку 1 выгодно уступить Игроку 2 некоторое количество товара 1 в обмен на товар 2.

Рассмотрим решение задачи о дуополии.

В этой задаче две фирмы сталкиваются с проблемой удовлетворения спроса на некоторый товар. Объем спроса зависит от уровня назначаемых цен и описывается функцией (ей соответствует нисходящая линия).

Объем предложения товара каждой из фирм так же зависит от уровня цен, а в микроэкономике описывается и ; эти функции определяются уровнем предельных издержек каждой из фирм.

Для простоты предположим, что фирма 1 и фирма 2 имеют одинаковые функции предложения .

Поиск решения в задаче о дуополии (т.е. определение уровня цен и объемов предложения каждой из фирм) базируется на принципах общих для решения задач теории игр: каждая из сторон располагает информацией о себе и своем партнере (в данном случае – о функциях предложения каждой из фирм), об условиях игры (в данном случае – о функции спроса) и действует , исходя из предположения, что ее партнер располагает такой же информацией и действует рационально (т.е. стремится максимизировать свой доход).

Если фирма 1 назначит цену на предлагаемый ею товар , а фирма 2 примет эту цену, то фирма 1 сможет придать объем товара равный .

Функция - называется остаточной функцией спроса, с которой сталкивается Фирма 1. Поскольку величины описывает объем спроса, приходящейся только на продукцию Фирмы 1, то она получит максимум дохода, полностью удовлетворив этот спрос, т.е. при условии, что .

В итоге Фирма 1, опираясь на имеющуюся у нее информацию, решает задачу поиска равновесного уровня цен , при которых .

Аналогично задачу поиска равновесных цен решает фирма 2 , учитывая, что , мы получим, что в ситуации равновесия . А доход каждый из фирм будет равен .

Таким образом, в задаче о дуополии фирмы должны найти такой уровень цен , при котором они могут полностью удовлетворить спрос, на продукцию распределив между собой производство этой продукции поровну и получив при этом одинаковый.

Уровень равновесных цен и объем предложенный каждой из фирм определяет в данной задаче ситуацию равновесия по Нэшу.

В итоге, проблемы рыночного взаимодействия близки к проблемам теории игр и могут быть эффективно описаны и исследованы в ее терминах.

Позиционные игры

Рассмотрим пример анализа рыночного поведения с помощью теории игр, когда задача по своей структуре несколько отличается от задач рассмотренных ранее.

Предположим следующую ситуацию.

На рынке некоторого продукта доминирует производитель (Фирма 1), и монопольное положение приносит ему 12 млрд. руб. прибыли. Высокая прибыль в данном секторе привлекает других производителей, в частности фирма 2 решает вопрос: построить ли ей свое предприятие и начать на нем производство такого же товара? Однако известно: что Фирма 1 может предпринять некоторые действия в ответ на вторжение.

С одной стороны Фирма 1 может снизить объем своего производства, уступая часть рынка Фирме 2, и деля с ней прибыль – так как это происходило на примере фирм – олигополистов. В этом случае каждая из фирм получит по 6 млрд. руб. прибыли.

С другой стороны фирма 1 может сохранить объем производства. В этом случае рост совокупного предложения товара фирмами 1 и 2 снизит цену на этот товар, и как следствие прибыль Фирмы 1 упадет до 5 млрд. руб. Одновременно снижение цен приведет к тому, что Фирма 2, сделавшая предварительные затраты для выхода на новый для нее рынок, понесет чистые убытки: она потеряет на этом деле 2 млрд. руб.

В случае если Фирма 2 воздерживается от вступления на рынок, она ничего не выигрывает и не проигрывает (ее прибыль 0 млрд. руб.), а Фирма 1 продолжает получать прибыль в 12 млрд. руб.

Если же Фирма 1 вдруг решит в этой ситуации снизить объем своего производства, ее прибыль упадет до 8 млрд. руб.

В принципе сформированная неантагонистическая игра двух лиц может быть описана следующей матрицей выигрышей (первыми указаны выигрыши фирмы 1 в млрд.руб.)

Стратегия Фирмы 1
Сохранить объем производства	Снизить объем производства

Замечание. Описанная игра по своим условиям отличается от рассмотренных ранее. В предыдущих задач игроки принимали свои решения одновременно, не зная о решении партнера (это весьма существенно), то в данной игре Фирма 1 принимает решения, уже зная о решении избранном Фирмой 2, в ответ она действия Фирмы 2, и это в корне меняет ситуацию.

Игры подобного класса, где задается последовательность принятия решений игроками, называются позиционными играми. Число игроков и шагов в них может равняться 2 (как в рассмотренном примере), 3 и т.д. К позиционным многошаговым играм двух лиц, где игроки принимают решения, зная обо всех предыдущих решениях партнера, можно отнести, например, шахматы и шашки.

В силу отмеченных особенностей структуру позиционной игры более наглядно представляет дерево решений (или в общем случае граф решений), приводящее игроков из исходной позиции в конечные.

Описанную игру Вступление на рынок можно представить следующим деревом, ветви которого соответствуют решениям партнеров, а у каждой из висячих вершин указаны выигрыши игроков (первыми указаны выигрыши Фирмы 1, в млрд. руб.).

В позиционной игре необходимо учитывать, что Фирма 1 принимает решение, уже зная о решении, принятом Фирмой 2, которая должна сделать первый шаг. При этом менеджеры Фирмы 2 могут привести доводы: «Если мы не вступим на рынок со своей продукцией, то в любом случае ничего не потеряем. С другой стороны, если мы решим внедрить на рынок, не исключено, что Фирма сохранит объем производства и для нас это обернется потерями 2 млрд. руб. Поэтому если следовать принципу максимизации своего минимального выигрыша Фирма 2 должна было бы избрать стратегию «Воздержаться от вступления на рынок» (в этом случае прибыль 0 млрд. руб.>-2 млрд. руб.)».

Эти, казалось бы, логичные рассуждения не учитывают одной из главных предпосылок теории игр – предположения о рациональном поведении игроков, стремящихся к максимизации своих выигрышей. В данном случае это заставляет менеджеров фирмы 2 задать себе вопрос: « А насколько вероятна реализация Фирмой 1 стратегии «Сохранить производство», если мы вторгнемся на рынок?» Ведь в этом случае Фирма 1 получит меньшую прибыль (5 млрд. руб.), чем в случае, если она снизит объем своего производства и поделится частью рынка с нами, получив при этом 6 млрд. руб.» В итоге, учитывая, что Фирма 1 будет вести себя рационально, её ответом на вступление Фирмы 2 должно стать снижение объема своего производства, вступления Фирмы 2 на рынок должно стать снижение объема своего производства, а не реализация угрозы сохранить прежний объем производства и подставить Фирму 2.

В данном случае в теории игр речь идет о правдоподобности угроз. В обсуждаемой игре угроза Фирмы 1 сохранить объем производства в ответ на вторжение Фирмы 2 на рынок является неправдоподобной, поскольку ее реализация приводит к меньшему выигрышу по сравнению с другими исходами.

Выигрыши

Вершины дерева игры называются позициями, непосредственно следующие за некоторой позицией называются альтернативами, позиции, не имеющие альтернатив, называются окончательными, а ведущие в них пути партиями (приведенная игра имеет четыре партии). Часть дерева решений, описывающая игру из некоторой позиции после нескольких начальных (ходов) шагов партнеров называется подыгрой и ее решение может представлять самостоятельную задачу.

Рассмотренная игра Вступление в рынок имеет две пары стратегий (две партии), удовлетворяющих условию равновесия по Нэшу: партия, когда Фирма 2 решает воздержаться от вступления на рынок, а Фирма 1 сохраняет объем своего производства и партия когда Фирма 2 решает вступить на рынок, а Фирма 1 в свою очередь снижает объем производства.

В каждой из этих двух партий отступление каждого из игроков от своей избранной стратегии приводит к уменьшению его выигрыша.

Возникает вопрос: реализация какой из этих двух равновесных партий наиболее вероятна?

В непозиционной игре обе партии равновероятны, т.к. игроки принимают решение одновременно и независимо друг от друга.

Учитывая этот факт можно утверждать, что наиболее вероятной будет реализация партии, когда Фирма 2 вступает на рынок, а Фирма 1 в ответ на это вторжение снижает объем своего производства: эта партия равновесна по Нэшу и, кроме того, учитывает степень правдоподобности угрозы Фирмы 1 сохранить объем своего производства и подавать, таким образом, Фирму 2.

Рассмотрим пример «Вступление на рынок» с измененными исходными данными. Дерево решений этой игры и выигрыша фирм в млрд. руб. представлены ниже.

Анализ игры, приведенной выше, позывает, что угроза Фирмы 1 сохранить объем своего производства является вполне правдоподобной: прибыль Фирмы 1 в этом случае (4млрд. руб.) не меньше, чем в случае, если она снизит объем своего производства и уступит часть рынка Фирме 2 (3 млрд. руб.). И вообще, стратегия Фирмы 1 «Сохранить производство» является доминирующей, т.е. следуя этой стратегии, Фирма 1 получает большую прибыль, чем в случае реализации другой своей стратегии «Снизить объем производства, - независимо от решений Фирмы 2.

Учитывая этот факт, Фирма 2, во избежание лишних потерь, должна избрать стратегию «Воздержаться от вступления на рынок».

Как следствие, в данном случае наиболее вероятной является реализация равновесной партии, когда Фирма 2 воздерживается от вступления на рынок, а Фирма 1 сохраняет объем своего производства, продолжая пользоваться монопольным положением.

Рассмотренный пример описывает случай так называемой устойчивой монополии, когда фирма-монополист в состоянии эффективно реализовать угрозу подавления своих потенциальных партнеров.

Это может объясняться естественными условиями производства, его технологическими особенностями, факторами, позволяющими фирме-монополисту гибко реагировать на действия противников (большой запас мощностей, реклама, вложение в перспективные исследования и т.д.). Поэтому вполне естественными выглядит желание государственных органов контролировать, а по возможности и ограничивать деятельность подобных фирм - устойчивых монополистов.

Вывод: Таким образом, проблемы рыночного взаимодействия близки к проблемам теории игр и могут быть эффективно описаны и исследованы в ее терминах.