Многоканальная система с отказами

Анализ такой СМО строится на базе классической задачи Эрланга (датского инженера, основателя теории СМО).

Имеется n каналов, на которые поступает поток заявок с интенсивностью 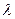. Поток обслуживаний имеет интенсивность 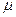. Требуется определить предельные вероятности состояний системы и показатели ее эффективности.

Система 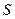(СМО) имеет следующие состояния: s₀, s₁, s₂,…,s_k,…,s_n, где s_k – состояние системы, когда в ней находится k заявок, т.е. занято k каналов. Граф состояния показан на рис.5.

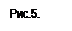
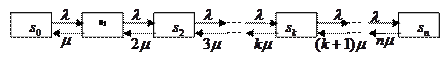
Поток заявок последовательно переводит систему из любого состояния в соседнее правое с одной и той же интенсивностью 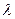. Интенсивность же потока обслуживаний, переводящих систему из любого правого состояния в соседнее левое, постоянно меняется в зависимости от состояния. Действительно, если СМО находится в состоянии s₂ (два канала заняты), то она может перейти в состояние s₁ (один канал занят), когда закончит обслуживание либо первый, либо второй канал, т.е. суммарная интенсивность их потоков обслуживаний будет 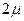и т.д.

Используя формулу (11) для схемы гибели и размножения, получим для предельной вероятности состояния s₀

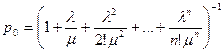(16)

где члены разложения 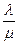, ,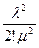…, 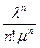будут представлять собой коэффициенты при p₀ в выражениях для предельных вероятностей p₁, p₂,…, p_n.

Величину 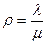называют параметром загрузки системы. Она выражает среднее число заявок, приходящее за среднее обслуживания одной заявки. Теперь

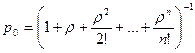(17)

, ,…,

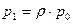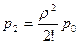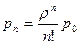
Формулы (7.17) получили название формул Эрланга в честь основателя теории массового обслуживания.

Доля потерянных требований или вероятность отказа СМО есть предельная вероятность того, что все n каналов системы будут заняты

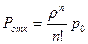(18)

Относительная пропускная способность – вероятность того, что заявка будет обслужена

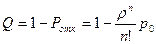(19)

Абсолютная пропускная способность

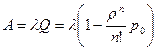(20)

Среднее число занятых каналов с учетом того, что каждый занятый канал обслуживает в среднем 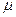заявок в единицу времени равно

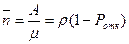( 21)

Пример 4. Определить показатели системы массового обслуживания в условиях примера 3, если в магазине принимают заказы по двум телефонам.

Решение. Параметр загрузки системы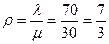

Доля потерянных заказов

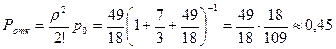
Пропускная способность системы

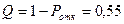
Абсолютная пропускная способность

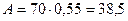
Среднее число занятых каналов

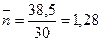
Оба телефона заняты, и заказ невозможно сделать в 45% случаев. Однако, в среднем лишь один из двух обслуживающих работников занят оформлением заказов, а второй бездействует.

Показатель 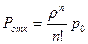означает долю времени, когда в системе заняты все n каналов. Наряду с Р_отк можно определить полную группу показателей 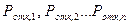, отражающих долю времени, когда в системе заняты обслуживанием 0, 1,…, n каналов. При этом р₀ называют долей времени простая n-канальной системы.

Пример 5. В условиях примера 3 определить долю времени занятости обслуживанием одновременно двух работников магазина, одного работника и долю времени, когда оба работника свободны от обслуживания.

Решение. Доля времени простоя:

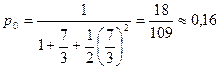
Доля времени занятости одного и двух работников соответственно

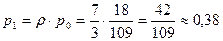
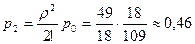
СМО с очередью