Достаточное условие экстремума.

Пусть функция определена в критической точке x₀ и дифференцируема в некоторой окрестности этой точки, за исключением, может быть, самой x₀. Если «при переходе» через точку x₀ слева направо производная меняет знак с плюса на минус, то x₀ – точка максимума; с минуса на плюс – точка минимума.

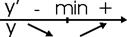
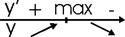
Пример: Исследовать функцию на монотонность и найти точки экстремума.

.

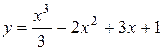1. Область определения функции D(y)=R.

2. .

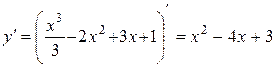Критические точки: 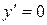. 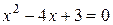Þ , .

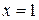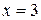x	(-∞;1)	x=1	(1;3)	x=3	(3;+∞)
	+		–		+
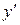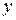	возрастает	max	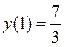убывает	min y(3)=1	возрастает

Наибольшее и наименьшее значения функции на отрезке.

Пусть функция 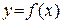определена и непрерывна на замкнутом промежутке [a;b] и имеет внутри этого промежутка конечную производную.

Тогда по второй теореме Вейерштрасса она на этом отрезке принимает свои наибольшее и наименьшее значения.

Очевидно, что эти значения могут достигаться либо в критических точках, либо на концах отрезка.

Поэтому для нахождения наибольшего и наименьшего значений функции применяют следующий алгоритм решения:

1. Находим критические точки функции. Отбираем те точки, которые принадлежат данному отрезку.

2. Вычисляем значения функции в найденных точках.

3. Вычисляем значения функции на концах отрезка.

4. Из полученных значений функции выбираем наибольшее и наименьшее.

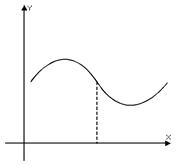
Выпуклые и вогнутые функции.

Пусть функция 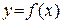дифференцируема на интервале (a;b). Тогда на этом интервале в каждой точке графика функции существует касательная, причем не параллельная оси OY.

Определение: Функция называется выпуклой, если ее график лежит над любой касательной, проведенной к этому графику.

Определение: Функция называется вогнутой, если ее график лежит под любой касательной, проведенной к этому графику.

На разных участках промежутка функция может быть выпуклой или вогнутой.

Признак выпуклости.

Пусть функция 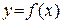имеет на интервале (a;b) непрерывную производную второго порядка. Если 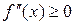, то функция выпукла на промежутке (a;b). Если 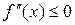, то функция вогнута на промежутке (a;b).

Замечание: Условие 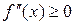( 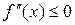) является не только достаточным, но и необходимым для выпуклых (вогнутых) функций.

Определение: Точка, отделяющая промежуток выпуклости функции от промежутка ее вогнутости, называется точкой перегиба.

Необходимые условия существования точки перегиба функции.

Пусть функция 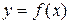в точке x₀ имеет точку перегиба. Если в этой точке существует производная второго порядка, то она обращается в ноль 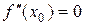или не существует.

Точки перегиба следует искать среди точек, вторая производная которых равна нулю (y²=0) или не существует. Такие точки называются критическими точками второго рода.

Достаточное условие точки перегиба функции.

Пусть 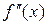непрерывна в окрестности точки 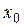, за исключением, может быть, самой точки 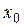. Если «при переходе» через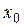 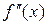меняет знак, то точка 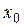— точка перегиба.

Пример: Исследовать функцию на перегиб. .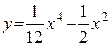

D(y)=R.

; .

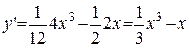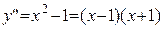Критические точки второго рода:

: ;

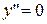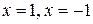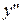не существует: точек нет.

При переходе через точки 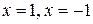вторая производная 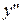меняет знак.

Þ 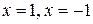— точки перегиба.

Асимптоты графика функции.

Определение: Прямая l называется асимптотой графика функции 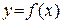, если расстояние от точки М на графике до прямой l стремится к нулю при удалении точки М по графику функции от начала координат.

Асимптоты бывают вертикальные, горизонтальные, наклонные.

Вертикальной асимптотой называется прямая x=a, если .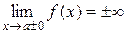

Находят вертикальную асимптоту по точкам разрыва второго рода (бесконечный разрыв).

Наклонной асимптотой называется асимптота, уравнение которой имеет вид: .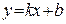

Оказывается, что если 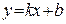является асимптотой, то 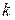и 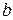в уравнении определяются следующим образом , .

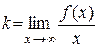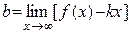Замечание 1: Чтобы у кривой были наклонные асимптоты, нужно, чтобы соответствующие пределы в определении k и b были конечными, причем предел при x→+∞ и предел при x→-∞ нужно вычислять отдельно.

Замечание 2: Если k=0, то y=b. Наклонная асимптота в этом случае называется горизонтальной.

Замечание 3: Кривая никогда не пересекает вертикальную асимптоту, а горизонтальные и наклонные асимптоты кривая может пересекать и даже бесконечное число раз.

Пример: Найти асимптоты графика функции .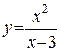

D(y): x¹3.

Þ x=3 – точка разрыва.

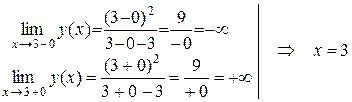— вертикальная асимптота.

= ;

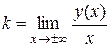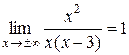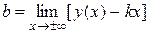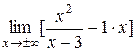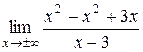= = = =3 Þ .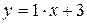

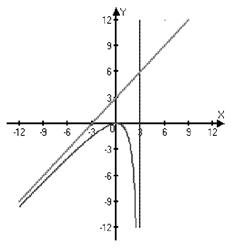
Þ 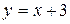— наклонная асимптота.

Схема полного исследования функции.

1. Определить естественную область D(y) определения функции.

2. Исследовать на четность и нечетность.

3. Найти точки пересечения графика функции с осями координат.

4. Найти асимптоты.

5. Найти интервалы возрастания и убывания функции, точки экстремума.

6. Найти интервалы выпуклости графика, точки перегиба.

7. Построить график функции.