Решение задачи Коши операционным методом

Операционное исчисление – один из наиболее экономичных методов интегрирования линейных дифференциальных уравнений с постоянными коэффициентами. При решении операционным методом задача интегрирования линейного дифференциального уравнения с постоянными коэффициентами сводится к задаче о решении алгебраического уравнения.

Рассмотрим задачу Коши:

где – искомое решение, – постоянные коэффициенты.

Алгоритм решения такой задачи операционным методом состоит в следующем. Обозначим и изображения для и . По основным свойствам преобразования Лапласа, переходя к изображениям, получим

или , где и – многочлены. Отсюда , и искомое решение задачи Коши является оригиналом .

Рассмотрим решение задачи Коши на примере.

Пример 3. Решить задачу Коши: , , операционным методом.

1) Найдем изображение для правой части уравнения

2) Запишем изображение левой части уравнения. Обозначим через изображение . Тогда изображение равно , изображение равно . Следовательно, изображение равно . Найдем изображение первой части и приравняем полученные изображения.

3)Определим и решим алгебраическое уравнение относительно .

Введите ключевое слово Given, затем введите правую часть уравнения, знак символьного равенства (<Ctrl>+<=>), правую часть уравнения, функцию

Find аргумента и щелкните вне выделяющей рамки

4) Выполним обратное преобразование Лапласа – найдем решение задачи

Коши

5) Определим найденное решение как функцию переменной

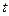
Подставим найденное решение в левую часть уравнения и упростим

полученное решение.

6) Выполним проверку.

Для этого дважды дифференцируем решение и подставим в данное по условию уравнение

7) Проверим начальное условие

◄

Пример 4. Решить задачу Коши операционным методом:

►Находим изображение левой части

Ниже приведен фрагмент решение уравнения в Mathcad

◄

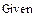Пример 5. Решить систему уравнений

►Переходим к изображениям:

Ниже приведен фрагмент решение системы уравнения в Mathcad

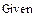План выполнения работы

1. Выполните примеры 1−5 из описания.

2. Найти изображения функций

а) ; б)

Выполнить проверку.

3. Найти оригинал по изображению

а) ; б)

Выполнить проверку.

4. Решить уравнение и систему из расчетной работы по варианту.

Контрольные вопросы

1. Как с помощью символьных операций можно находить оригинал и изображение Лапласа?

2. Каков алгоритм решения задачи Коши операционным методом?

Лабораторная работа №7

«Аппроксимация в MathCAD »

Цель работы: познакомиться с интерполяцией и аппроксимацией.

Обработка данных - важная сфера применения компьютерной математики. Для представления физических закономерностей, а также для проведения научно-технических расчетов часто используются зависимости вида у(х), причем число заданных точек ограничено. Неизбежно возникает задача приближенного вычисления значений функций в промежутках между узловыми точками (интерполяция) и за их пределами (экстраполяция). Эта задача решается аппроксимацией и интерполяцией исходной зависимости, то есть ее подменой какой либо достаточно простой функцией. Важной задачей математической обработки подобных данных является их представление в виде некоторой математической зависимости, допускающей проведение над нею обычных математических операций, например вычисление у(х) при х, не совпадающих с исходными (узловыми) точками, интегрирование или дифференцирование функций, проведение их статистической обработки (сглаживания или фильтрации) и т. д.. Данные эксперимента, получаемые на различных физических или электронных измерительных установках, задаются в табличном виде, т. е. рядом значений х и соответствующих им значений у.

Пусть известны значения функции на отрезке

x	x0	x1	…	xn
y	y0	y1	…	yn

Функция называется интерполяционной для на , если ее значения в заданных точках , называемых узлами интерполяции, совпадают с заданными значениями функции .

В зависимости от вида функции интерполяция называется линейной, квадратичной или кубической.

В систему MathCAD встроены функции линейной и сплайн-интерполяции, при которых отдельно на каждом промежутке функция представляется отрезком прямой, то есть линейной функцией или кубическим многочленом. Аппроксимирующая функция находится так, чтобы обеспечить стыковку в узловых точках значений функции, и ее первых двух производных (что и дает необходимую гладкость графика функции).

При небольшом числе узловых точек линейная интерполяция оказывается довольно грубой. Гораздо лучшие результаты дает сплайн-интерполяция. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закрепленную в узловых точках.