Решение задачи коши для обыкновенных дифференциальных уравнений 1-го порядка
Л Е К Ц И Я № 6
Обыкновенное дифференциальное уравнение 1-го порядка
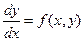
 связывает независимую переменную x, искомую функцию y и её производную. Решение дифференциального уравнения заключается в отыскании функции y = y(x), обращающей это уравнение в тождество на конечном или бесконечном интервале (a, b). Различают общее и частные решения дифференциального уравнения. Общее решение уравнения имеет вид y = y(x, C), где C – произвольная постоянная интегрирования. Его графическим отображением является семейство кривых (рис.1), называемых интегральными. Каждая интегральная кривая является отображением частного решения, соответствующего своему значению постоянной C. Для выделения частного решения из множества кривых общего решения необходимо задать начальное условие
связывает независимую переменную x, искомую функцию y и её производную. Решение дифференциального уравнения заключается в отыскании функции y = y(x), обращающей это уравнение в тождество на конечном или бесконечном интервале (a, b). Различают общее и частные решения дифференциального уравнения. Общее решение уравнения имеет вид y = y(x, C), где C – произвольная постоянная интегрирования. Его графическим отображением является семейство кривых (рис.1), называемых интегральными. Каждая интегральная кривая является отображением частного решения, соответствующего своему значению постоянной C. Для выделения частного решения из множества кривых общего решения необходимо задать начальное условие
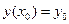 .
.
 Такая постановка задачи отыскания решения дифференциальных уравнений называется задачей Коши (A.L.Cauchy, 1789–1857). Для существования единственного решения задачи Коши необходимо и достаточно существование и ограниченность правой части дифференциального уравнения f(x, y) и её частной производной ¶f(x, y)/¶y в некоторой окрестности начальной точки (x0, y0).
Такая постановка задачи отыскания решения дифференциальных уравнений называется задачей Коши (A.L.Cauchy, 1789–1857). Для существования единственного решения задачи Коши необходимо и достаточно существование и ограниченность правой части дифференциального уравнения f(x, y) и её частной производной ¶f(x, y)/¶y в некоторой окрестности начальной точки (x0, y0).
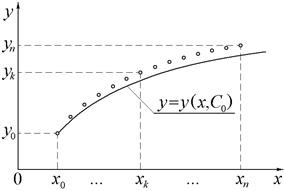
 Для численного решения задачи Коши существует множество методов, которые условно делятся на две группы: одношаговые и многошаговые. Все эти методы позволяют получить искомое решение дифференциального уравнения в виде таблично заданной функции, в той или иной мере согласующееся с истинным частным решением (см. рис.2). Эти группы методов различаются объёмом информации, которая используется для вычисления координат очередной точки табличной функции. Одношаговые методы используют значения функции и её производной только в одной предыдущей точке, в то время как многошаговые – в нескольких. К одношаговым методам решения задачи Коши относятся метод Эйлера, модифицированный метод Эйлера, методы Рунге–Кутта и другие.
Для численного решения задачи Коши существует множество методов, которые условно делятся на две группы: одношаговые и многошаговые. Все эти методы позволяют получить искомое решение дифференциального уравнения в виде таблично заданной функции, в той или иной мере согласующееся с истинным частным решением (см. рис.2). Эти группы методов различаются объёмом информации, которая используется для вычисления координат очередной точки табличной функции. Одношаговые методы используют значения функции и её производной только в одной предыдущей точке, в то время как многошаговые – в нескольких. К одношаговым методам решения задачи Коши относятся метод Эйлера, модифицированный метод Эйлера, методы Рунге–Кутта и другие.
Метод Эйлера (L.Euler, 1768)
Он является старейшим методом решения задачи Коши и заключается в последовательном применении следующих формул
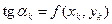 ,
,
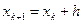 ,
, 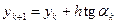 ,
,
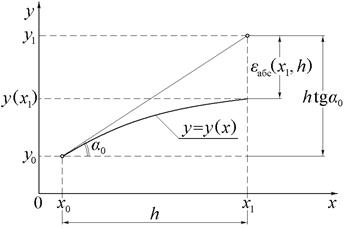 геометрическая интерпретация которых при k = 0 представлена на рис.3. В точке (x0, y0)вычисляется значение производной dy/dx через f(x, y), которое определяет тангенс угла наклона касательной к графику точного решения задачи Коши. Следующая точка численного решения определяется как точка на этой касательной с абсциссой x1 = x0+ h. В компактном виде эти соотношения записываются следующим образом
геометрическая интерпретация которых при k = 0 представлена на рис.3. В точке (x0, y0)вычисляется значение производной dy/dx через f(x, y), которое определяет тангенс угла наклона касательной к графику точного решения задачи Коши. Следующая точка численного решения определяется как точка на этой касательной с абсциссой x1 = x0+ h. В компактном виде эти соотношения записываются следующим образом
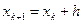 ,
,
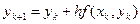 .
.
Метод Эйлера относится к методам первого порядка точности, поскольку его решение совпадает с истинным только в том случае, когда последнее является линейной функцией y = a1+ a2x. Его абсолютная погрешность εабс(xk+1, h) на каждом шаге пропорциональна величине h2. Это обусловлено тем, что в качестве направления, определяющего положение следующей точки численного решения, используется касательная в левой точке каждого отрезка [xk, xk+1].
На рис.3 видно, что для получения более точного численного решения недостаточно знания параметров функции в единственной левой точке отрезка [xk, xk+1]. Требуется собрать дополнительную информацию о её поведении на отрезке интегрирования для отыскания решения при x = xk+1 с меньшей погрешностью. Для этого можно использовать некоторые промежуточные направления, определяемые касательными к графику неизвестного точного решения в характерных точках рассматриваемого отрезка (крайние точки, середина отрезка и т.д.).
