Понятие множества. Подмножества.

Понятие множества. Подмножества.

Множество – совокупность объединенных по некоторым общим признакам различных предметов, называемых элементами множества. (Опр. Кантора – «Многое, мыслимое как целое»). Элемент множества называется кортежем.

X = {x, y, z …}

X = {x₁, x₂, x₃, …}

X = {x_i, i = [1,n]}
Также множество можно задать характеристическими свойствами – X = {x: x – целое число }

Ординарные множества не включают себя в качестве своего элемента, экстраординарные – включают. Парадокс Рассела : пускай О – множество ординарных множеств. Если оно ординарное, то оно включает себя в качестве ординарного, но тогда оно становится экстраординарным. В таком случае считается, что множество О не существует. Оно не пустое, а именно не бывает. Также не может быть «множества всех множеств».

Понятие подмножества возникает каждый раз, когда приходится рассматривать некоторое множество не самостоятельно, а как часть другого более широкого множества.
Теорема Кантора доказывает, что количество элементов множества всегда меньше количества элементов множества его подмножеств. (То же относительно мощности.)

Если каждый элемент y множества Y является элементом множества X, то Y называется подмножеством множества X.

Y⊂X – собственное подмножество (строгое включение, т.е. множества Y и X не совпадают и мощность Y меньше мощности X.)

Y⊆X – подмножество. Если Y включает в себя X, а X включает в себя Y, то множества совпадают.
Теоремы о необходимых и достаточных условиях – теоремы о совпадении двух множеств. (Напр., для делимости на 10 числу необходимо и достаточно иметь последней цифрой 0.)
У каждого n-элементного множества 2ⁿ подмножеств.

∅ - пустое множество, не содержащее элементов. Любое множество содержит пустое подмножество.

Универсальное множество – в него входят все остальные множества, которые рассматриваются в данной задаче. (Или же множество, содержащее все объекты и все множества. Универсальное множество единственно.)

|X| - число элементов конечного множества.

Операции над множествами.

Объединение (сложение): X∪Y = {x: x∈X или x∈Y}
Обладает свойствами: коммутативности (перестановочности), ассоциативности (сочетаемости).
Если объединённое семейство множеств содержит заданное множество, то это семейство называется покрытием заданного множества. При этом каждое множество семейство – блок покрытия. Если при этом ни у одного из блоков покрытия нет одинаковых с другим блоком элементов, то покрытие можно назвать разбиением, а блоки – блоками разбиения.

Пересечение: X⋂Y = {x: x∈X и x∈Y} (Если нет общих элементов, то = ∅) (Свойства: коммутативность, ассоциативность)
Операции объединения и пересечения связаны законами дистрибутивности (распределительными).
Для операций объединения и пересечения действуют законы Моргана.

Разность: X/Y = {x: x∈X и x∉Y} (Элемент, который есть в х, но нет в у).

Симметричная разность (элементы, которые есть в Х, но нет в У + наоборот)

Декартово произведение – совокупность всех упорядоченных пар (х,у) таких, что х∈Х, у∈У. (Примером дек. произв. можно назвать множество точек: {1,2}×{2,6} {(1,2), (1,6), (2,2), (2,6)}
Х×У = {(x,y): x∈X, y∈Y}
При совпадении Х и Y – декартова степень.

Конечные и бесконечные множества. Мощность множества.

Конечное – содержит конечное число элементов. Только элементы конечных множеств могут быть заданы в любом порядке.

Бесконечное – содержит бесконечно много элементов. Чтобы сравнить бесконечные множества, нужно установить взаимно-однозначное соответствие. Если это удаётся, то множества равномощные, иначе одно из них имеет большую мощность.
Бесконечное множество может включать в себя другое бесконечное множество. (Комплексные числа включают в себя вещественные.)

|X| - число элементов (для конечного множества); мощность – для бесконечного множества.
Теорема Кантора доказывает, что количество элементов множества всегда меньше количества элементов множества его подмножеств.
Множества натуральных и целых чисел равномощны. Множество вещественных чисел больше множества натуральных даже на отрезке [0; 1].

Комбинаторика и множества.

Комбинаторику можно назвать теорией конечных множеств. Как теория множеств комбинаторика даёт методы, как, зная количество элементов некоторых множеств, вычислить количество элементов других множеств, составленных из первых с помощью некоторых операций.
Расположение элементов некоторого множества называют комбинаторной конфигурацией.

· формула включений-исключений

· чтобы подсчитать количество подмножеств с разным кол-вом элементов используют формулы комбинаторики (сочетания без повторений)

· У каждого n-элементного множества 2ⁿ подмножеств.

Множество целых чисел.

Все положительные или отрицательные числа, не являющиеся дробями, и нуль.
У каждого числа есть симметричное от начала координат (противоположное ему).
Отрицательные числа впервые появились в Китае, в Европе начали использоваться со времён Рене Декарта.

Z = {… , -3, -2, -1, 0, 1, 2, 3, …}

Формула Муавра.

Нужна для возведения компл. числа в степень и извлечения корня n-ной степени. (Нужно сначала представить компл. число в тригонометрической форме).

zⁿ=|z|ⁿ(cos(nα) + i sin(nα)

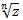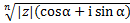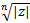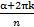= = (cos + i sin )
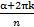Для любого компл. числа есть n корней n-ной степени.
k – меняется от 0 до n-1 в зависимости от номера корня (т.е. если n=2 то, всего 2 корня, а k может быть 0 и 1)

14. Последовательности и их пределы.

Числовую функцию f(n)=a, заданную на множестве натуральных чисел, называют числовой последовательностью. Говорят, что последовательность задана, если каждому натуральному числу n по некоторому закону f поставлено в соответствие число f(n).
Если закон f задан формулой – аналитическое задание последовательности. При нём записывают аналитическое выражение для общего члена a_n.
Способ построения очередного члена последовательности по предыдущим называется рекуррентным.

Существуют убывающие и возрастающие последовательности.

Ограниченная сверху последовательность – существует число M такое, что a_n<M для всех n.

Ограниченная снизу последовательность – существует число M такое, что a_n>M для всех n.

Ограниченная последовательность – последовательность, ограниченная и сверху, и снизу.

Последовательность {x_n} – бесконечно большая, если для любого A>0 (сколь бы большим его ни взяли) существует номер N такой, что для всех членов последовательности с номерами n>N выполняется |x_n|>A.

Последовательность {a_n} – бесконечно малая: для всех n>N выполняется |a_n|< 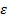( 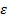– очень малое).

Последовательность {a_n} сходится к числу A, если для любого сколь угодно малого 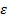>0 можно указать такое n₀( 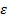)∈N, что для всех n>n₀ выполняется |a_n – A|< .

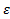Если последовательность имеет пределом точку A, то для всех номеров последовательности, начиная с некоторого n₀, члены последовательности находятся внутри отрезка 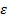(A- ; A+ 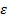), называемого 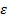-окрестностью числа A.

Почти все числа {a_n} попадают в 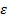-окрестность.

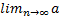_n = A – предел.

Если последовательность не имеет конечного предела или не имеет предела вообще, то ее называют расходящейся.

Пределы функций.

По простому – к чему стремится y (функция), когда x (аргумент) стремится к заданной величине.

Пусть f(x) – функция непрерывного аргумента. Число A – предел функции y = f(x) при x 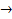x₀, если для каждого сколь угодно малого ε>0 можно указать зависящее от ε число δ(ε)>0 такое, что для всех x, удовлетворяющих |x₀ – x|<δ имеет место неравенство |A – f(x)|<ε. (Определение Коши.)

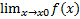=A

Число А называют пределом функции f(x) при х 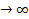, если для каждого сколь угодно малого числа ɛ >0 можно указать зависящее от него число δ(ɛ) > 0 такое, что для всех x, удовлетворяющих неравенству |x|>δ, имеет место неравенство |A - f(x)|<ɛ.

Число А называется правым пределом функции f(x) в точке x₀, если для каждого сколь угодно малого числа ɛ>0 можно указать зависящее число ɗ(ɛ) > 0 такое, что для всех x, удовлетворяющих неравенству x-x₀ < δ, имеет место неравенство |A-f(x)|<ɛ.

A = f (x0 +0) =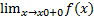

Левый предел: A = f (x0 -0) =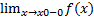

Правый и левый пределы – односторонние пределы функции в точке.

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция оказывается непрерывной (в данной точке).

Свойства пределов функций.

· Если предел функции существует, то он единственен.

· Предел постоянной величины равен самой постоянной.

· Периодические функции не имеют пределов на бесконечности.

· Если при 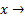a существуют конечные пределы f(x) и g(x), то:

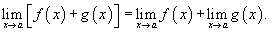
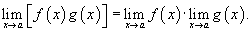
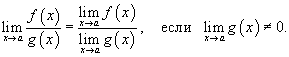
19. Бесконечно малые и бесконечно большие функции.

Если при x 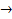x₀ функция f(x) стремится к 0, то ее называют бесконечно малой в окрестности точки x₀.

Если f(x) при x 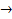x₀ стремится к 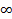, то она называется бесконечно большой в окрестности точки x₀.

( http://www.mathprofi.ru/beskonechno_malye_funkcii_zamechatelnye_ekvivalentnosti.html )

Правила дифференцирования.

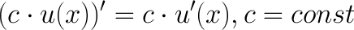
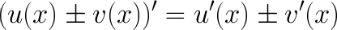
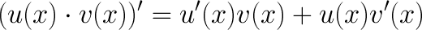
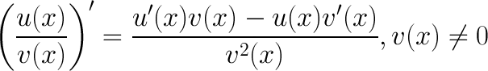
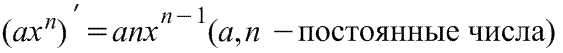
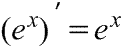
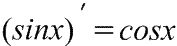
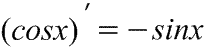
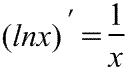
(f(g(x)))’ = f’(g(x)) g’(x). – производная сложной ф-ции.

Интеграл Римана.

Интеграл Римана = определенный интеграл.

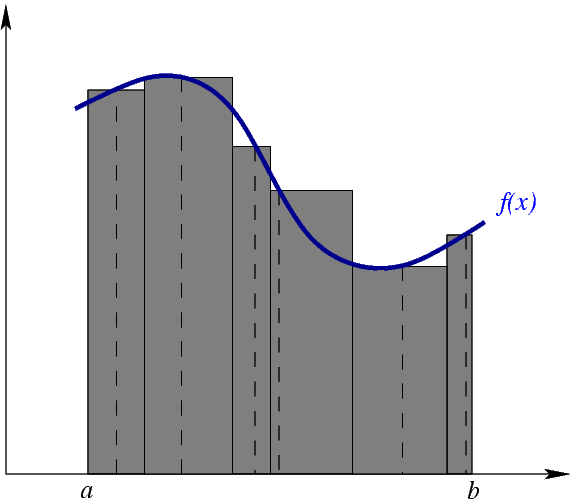
Из википедии: «Риман формализовал понятие интеграла, разработанное Ньютоном и Лейбницем, как площади подграфика (фигуры, заключенной между графиком функции и осью абсцисс). Для этого он рассмотрел фигуры, состоящие из нескольких вертикальных прямоугольников и получающиеся при разбиении отрезка (см. рисунок). Если при «размельчении» разбиения существует предел, к которому сходятся площади таких фигур (интегральные суммы), этот предел называется интегралом Римана функции на отрезке.»

Вообще определенный интеграл – это площадь криволинейной трапеции.

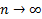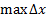Из учебника: «Если независимо от способа разбиения отрезка [a,b] на части, для функции f(x) существует конечный предел интегральной суммы при и _i 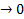, то этот предел называется определенным интегралом f(x) от a до b, а сама функция f(x) – интегрируемой на отрезке [a,b].»

Обозначается так:

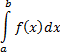
a, b – нижний и верхний пределы интеграла.

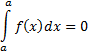
Интеграл существует для всех непрерывных функций.

Функциональные ряды.

Функциональный ряд – ряд, членами которого являются функции от аргумента x:

u₁(x) + u₂(x) + u₃(x) + … + u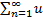_n(x) + … = _n(x).

Если зафиксировать x=x₀, то получим числовой ряд u₁(x₀) + u₂(x₀) + u₃(x₀) + … + u_n(x₀) + …

Если при x= x₀ числовой ряд сходится, то x₀ – точка сходимости функционального ряда.

Область сходимости – множество всех точек сходимости.

Сумма ряда в x= x₀: u₁(x₀) + u₂(x₀) + u₃(x₀) + … + u_n(x₀) + … = S(x₀).

Функциональный ряд 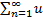_n(x) называется абсолютно сходящимся, если сходится ряд 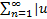_n(x)|.

Определение области сходимости:

· Признаки сравнения

· Признак Даламбера

· Признак Коши

39. Степенные ряды и их свойства.

Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:

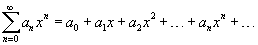
Часто рассматривается также ряд, расположенный по степеням (x − x₀), то есть ряд вида

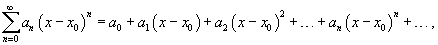
где x₀ − действительное число.

Свойства:

Рассмотрим степенной ряд

с₀ + с₁ х + с₂ х² + ... + с_{n x}ⁿ + ... , (10.1)

имеющий радиус сходимости R>0 (R может равняться 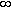). Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначим ее через S(x). Тогда можно записать равенство

S(x) = c₀ + c₁ x + c₂ x² + ... + c_n xⁿ + ... , (10.2)

понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции S(x) в этой точке. В этом же смысле будем говорить, что ряд (10.1) сходится к функции S(x) на интервале сходимости. Вне интервала сходимости равенство (10.2) не имеет смысла.

Можно доказать, что сумма степенного ряда S(x) непрерывна и дифференцируема на любом отрезке [a, b] внутри интервала сходимости.

Равенство (10.2), справедливое в интервале сходимости степенного ряда, называют разложением S(x) в степенной ряд.

Для степенных рядов справедливы следующие утверждения:

Теорема 1.

Степенной ряд в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны S`(x), S``(x), ... , S⁽ⁿ⁾(x).

Теорема 2.

Степенной ряд можно неограниченное число раз почленно интегрировать в пределах от 0 до х, если х (-R; R), причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны .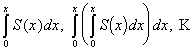

Теорема Абеля.

Если степенной ряд сходится при некотором x=x₀, где x₀ - число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что |x|<|x₀|. Наоборот, если ряд расходится при x=x0, то он расходится при всех значениях x таких, что |x|>|x₀|.

40. Область сходимости и радиус сходимости степенного ряда.

Радиус сходимости ряда – неотрицательное число R такое, что при |x|<R ряд сходится, а при |x|>R – расходится.

Интервал сходимости – (-R,R).

Найти R можно по признаку Даламбера (или признаку Коши).

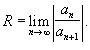
При x=±R ряд либо сходится, либо расходится (у каждого ряда по-своему).

Ряд Тейлора. Ряд Маклорена.

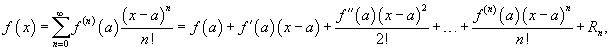
Если приведенное разложение сходится в некотором интервале x, т.е. 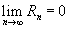, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.

Частный случай – ряд Маклорена (при a=0)

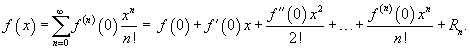
Выборки и разбиения.

Два подхода к комбинаторным схемам:
Выборка – с повторениями и без. (Сколькими способами можно вытащить r элементов из n элементов.)
Разбиение (в частности подход к сочетаниям) – сколькими способами можно разделить r элементов на n групп. (Напр., мальчики делят яблоки.)

Понятие множества. Подмножества.

Множество – совокупность объединенных по некоторым общим признакам различных предметов, называемых элементами множества. (Опр. Кантора – «Многое, мыслимое как целое»). Элемент множества называется кортежем.

X = {x, y, z …}

X = {x₁, x₂, x₃, …}

X = {x_i, i = [1,n]}
Также множество можно задать характеристическими свойствами – X = {x: x – целое число }

Ординарные множества не включают себя в качестве своего элемента, экстраординарные – включают. Парадокс Рассела : пускай О – множество ординарных множеств. Если оно ординарное, то оно включает себя в качестве ординарного, но тогда оно становится экстраординарным. В таком случае считается, что множество О не существует. Оно не пустое, а именно не бывает. Также не может быть «множества всех множеств».

Понятие подмножества возникает каждый раз, когда приходится рассматривать некоторое множество не самостоятельно, а как часть другого более широкого множества.
Теорема Кантора доказывает, что количество элементов множества всегда меньше количества элементов множества его подмножеств. (То же относительно мощности.)

Если каждый элемент y множества Y является элементом множества X, то Y называется подмножеством множества X.

Y⊂X – собственное подмножество (строгое включение, т.е. множества Y и X не совпадают и мощность Y меньше мощности X.)

Y⊆X – подмножество. Если Y включает в себя X, а X включает в себя Y, то множества совпадают.
Теоремы о необходимых и достаточных условиях – теоремы о совпадении двух множеств. (Напр., для делимости на 10 числу необходимо и достаточно иметь последней цифрой 0.)
У каждого n-элементного множества 2ⁿ подмножеств.

∅ - пустое множество, не содержащее элементов. Любое множество содержит пустое подмножество.

Универсальное множество – в него входят все остальные множества, которые рассматриваются в данной задаче. (Или же множество, содержащее все объекты и все множества. Универсальное множество единственно.)

|X| - число элементов конечного множества.

Операции над множествами.

Объединение (сложение): X∪Y = {x: x∈X или x∈Y}
Обладает свойствами: коммутативности (перестановочности), ассоциативности (сочетаемости).
Если объединённое семейство множеств содержит заданное множество, то это семейство называется покрытием заданного множества. При этом каждое множество семейство – блок покрытия. Если при этом ни у одного из блоков покрытия нет одинаковых с другим блоком элементов, то покрытие можно назвать разбиением, а блоки – блоками разбиения.

Пересечение: X⋂Y = {x: x∈X и x∈Y} (Если нет общих элементов, то = ∅) (Свойства: коммутативность, ассоциативность)
Операции объединения и пересечения связаны законами дистрибутивности (распределительными).
Для операций объединения и пересечения действуют законы Моргана.

Разность: X/Y = {x: x∈X и x∉Y} (Элемент, который есть в х, но нет в у).

Симметричная разность (элементы, которые есть в Х, но нет в У + наоборот)

Декартово произведение – совокупность всех упорядоченных пар (х,у) таких, что х∈Х, у∈У. (Примером дек. произв. можно назвать множество точек: {1,2}×{2,6} {(1,2), (1,6), (2,2), (2,6)}
Х×У = {(x,y): x∈X, y∈Y}
При совпадении Х и Y – декартова степень.