Множества и подмножества
Раздел 1. Множества.
Элементы и множества. Способы задания множеств. Сравнение множеств. Мощность множества. Операции над множествами и их свойства. Разбиение и покрытия. Булеан. Генерация всех подмножеств заданного универсума. Алгоритм построения бинарного кода Грея. Алгоритмы пересечения, объединения двух множеств и проверки включения слиянием.
Множества и подмножества.
Одними из основных, исходных понятий математики являются понятия множества и его элементов. Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. Можно сказать, что множество – это любая совокупность объектов. Объекты, из которых составлено множество называются его элементами. Элементы множества различны и отличимы друг от друга. Принадлежность элемента а множеству М обозначается а Î М (a принадлежит М); непринадлежность а множеству М обозначается а Ï М или а 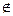 М.
М.
Множество А называется подмножеством множества В (обозначение А 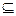 В; знак
В; знак 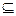 называется знаком включения), если всякий элемент А являётся элементом В. При этом говорят, что В содержит или покрывает А. Множества А и В равны, если их элементы совпадают, иначе говоря, если А
называется знаком включения), если всякий элемент А являётся элементом В. При этом говорят, что В содержит или покрывает А. Множества А и В равны, если их элементы совпадают, иначе говоря, если А 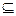 В и В
В и В 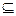 А. Второй вариант определения равенства множеств указывает и на наиболее типичный метод доказательства того, что данные множества равны, заключающийся в доказательстве сначала утверждения А
А. Второй вариант определения равенства множеств указывает и на наиболее типичный метод доказательства того, что данные множества равны, заключающийся в доказательстве сначала утверждения А 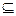 В («в одну сторону»), а затем В
В («в одну сторону»), а затем В 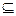 А («в другую сторону»). Форму утверждения о равенстве двух множеств имеют многие математические теоремы. Пример — тригонометрическая теорема, состоящая из двух утверждений: а) всякое решение уравнения sin х = 1 имеет вид p/2 ± kp; б) всякое число вида p/2 ± kp является решением уравнения sin х = 1.
А («в другую сторону»). Форму утверждения о равенстве двух множеств имеют многие математические теоремы. Пример — тригонометрическая теорема, состоящая из двух утверждений: а) всякое решение уравнения sin х = 1 имеет вид p/2 ± kp; б) всякое число вида p/2 ± kp является решением уравнения sin х = 1.
Если А Í В и А ¹ В, то А часто называется собственным, строгим или истинным подмножеством В (обозначение А Ì В; знак Ì называется знаком строгого включения).
Множества могут быть конечными (т. е. состоящими из конечного числа элементов) и бесконечными. Если элементы бесконечного множества можно перенумеровать, то оно называется счетным, иначе – несчетным (вещественные числа, комплексные числа). Число элементов в конечном множестве М называется мощностью М и часто обозначается ½М½. Мощность бесконечного множества — более сложное понятие.
Множество мощности 0, т. е. не содержащее элементов, называется пустым и обозначается Æ. Принято считать, что пустое множество является подмножеством любого множества. Пустое множество введено в математике для удобства и единообразия языка. Например, если исследуется множество объектов, обладающих каким-либо свойством и впоследствии выясняется, что таких объектов не существует, то гораздо удобнее сказать, что исследуемое множество пусто, чем объявлять его несуществующим. Утверждение «множество М непусто» является более компактной формулировкой равносильного ему утверждения «существуют элементы, принадлежащие М».
