Тема: Векторное произведение векторов
Векторное произведение векторов 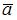 и
и 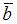 равно
равно  Тогда вектор
Тогда вектор  будет иметь координаты …
будет иметь координаты …
 |  |  | |
 |  | ||
 |  | ||
 |  |
Решение:
По свойствам векторного произведения векторов  В нашем случае
В нашем случае 
Тема: Векторное произведение векторов
Площадь параллелограмма, построенного на векторах  и
и  равна …
равна …
 |  |  | |
 |  | ||
 | |||
 |
Решение:
Площадь  параллелограмма, построенного на векторах
параллелограмма, построенного на векторах 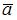 и
и 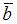 , равна модулю векторного произведения этих векторов, то есть
, равна модулю векторного произведения этих векторов, то есть  В нашем случае
В нашем случае

Следовательно, площадь параллелограмма равна

Тема: Векторное произведение векторов
Даны два вектора  и
и  где
где 
 угол между векторами
угол между векторами 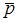 и
и 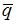 равен
равен  Тогда модуль векторного произведения векторов
Тогда модуль векторного произведения векторов 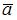 и
и 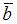 будет равен …
будет равен …
 |  | ||
 |  | ||
 | |||
 |  |
Решение:
Вычислим

Так как 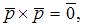

 то
то 
Тогда 

Тема: Смешанное произведение векторов
Векторы 
 и
и  линейно зависимы, если параметр
линейно зависимы, если параметр  равен …
равен …
 | – 6 | ||
| – 18 | |||
Решение:
Векторы 
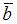 и
и  линейно зависимы, если их смешанное произведение равно
линейно зависимы, если их смешанное произведение равно  . Вычислим смешанное произведение векторов
. Вычислим смешанное произведение векторов 
 и
и  заданных своими координатами, по формуле
заданных своими координатами, по формуле 
В нашем случае  то есть вектора
то есть вектора 
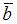 и
и  линейно зависимы при
линейно зависимы при 
Тема: Смешанное произведение векторов
Точки 

 и
и  лежат в одной плоскости, если параметр
лежат в одной плоскости, если параметр  равен …
равен …
 | |||
| – 1 |
Решение:
Точки 

 и
и  лежат в одной плоскости, если векторы
лежат в одной плоскости, если векторы 
 и
и  компланарны, то есть если их смешанное произведение равно 0. Смешанное произведение векторов
компланарны, то есть если их смешанное произведение равно 0. Смешанное произведение векторов 
 и
и  заданных своими координатами, находится по формуле
заданных своими координатами, находится по формуле 
В нашем случае 

 и
и 
то есть точки A, B, C и D лежат в одной плоскости при 
| |
1. Асимптоты гиперболы  задаются уравнениями вида
задаются уравнениями вида  .
.
Фокусы гиперболы, заданной каноническим уравнением  , имеют координаты
, имеют координаты  и
и  , где
, где  , а эксцентриситет
, а эксцентриситет  .
.
2. Каноническое уравнение эллипса имеет вид  ; фокусы эллипса имеют координаты
; фокусы эллипса имеют координаты  и
и  , где
, где  , а эксцентриситет
, а эксцентриситет  .
.
Пример. Мнимая полуось гиперболы  равна …
равна …
Выделим в уравнении  полный квадрат по переменной
полный квадрат по переменной  :
:  , или
, или  . Разделив обе части этого уравнение на 36, получим уравнение гиперболы в виде
. Разделив обе части этого уравнение на 36, получим уравнение гиперболы в виде  . Отсюда мнимая полуось
. Отсюда мнимая полуось  .
.
Тема: Кривые второго порядка
Фокусы эллипса имеют координаты  и
и  , а его эксцентриситет равен 0,6. Тогда каноническое уравнение эллипса имеет вид …
, а его эксцентриситет равен 0,6. Тогда каноническое уравнение эллипса имеет вид …
Решение:
Каноническое уравнение эллипса имеет вид  ; фокусы эллипса имеют координаты
; фокусы эллипса имеют координаты  и
и  , где
, где  , а эксцентриситет
, а эксцентриситет  .
.
Тогда  ,
,  ,
,  .
.
Следовательно, получаем уравнение  .
.
Задание # 46 - ошибка!
Вопрос:
Уравнением кривой второго порядка  на плоскости определяется …
на плоскости определяется …
Выберите один из 4 вариантов ответа:
1) эллипс
2) гипербола
3) парабола
4) пара пересекающихся прямых
Верный ответ (1 б.): 1;
Решение:
Выделим в уравнении  полный квадрат по переменной x:
полный квадрат по переменной x:  или
или  Разделив обе части этого уравнения на 10, получим уравнение вида:
Разделив обе части этого уравнения на 10, получим уравнение вида:  которое на плоскости определяет эллипс.
которое на плоскости определяет эллипс.
Задание # 47 - ошибка!
Вопрос:
Парабола, вершина которой находится в начале координат, симметрична относительно оси Ox и проходит через точку  Тогда уравнение параболы имеет вид …
Тогда уравнение параболы имеет вид …
Выберите один из 4 вариантов ответа:
1) 
2) 
3) 
4) 
Верный ответ (1 б.): 1;
Задание # 48 - ошибка!
Вопрос:
Эллипсы  и
и  пересекаются в точках с абсциссой, равной …
пересекаются в точках с абсциссой, равной …
Выберите один из 4 вариантов ответа:
1) 3
2) 1
3) 2
4) 4
Верный ответ (1 б.): 1;
Задание # 49 - ошибка!
Вопрос:
Уравнение директрисы параболы, проходящей через точки 
 и симметричной относительно оси Ox, имеет вид …
и симметричной относительно оси Ox, имеет вид …
Выберите один из 4 вариантов ответа:
1) -2
2) -4
3) 4
4) 2
Верный ответ (1 б.): 1;
Задание # 50 - ошибка!
Вопрос:
Соотношение  в прямоугольной декартовой системе координат задает …
в прямоугольной декартовой системе координат задает …
Выберите один из 4 вариантов ответа:
1) параболу
2) гиперболу
3) эллипс
4) окружность
Верный ответ (1 б.): 1;
Задание # 51 - ошибка!
Вопрос:
Точки  и
и  являются концами одного из диаметров окружности. Тогда уравнение окружности имеет вид …
являются концами одного из диаметров окружности. Тогда уравнение окружности имеет вид …
Выберите один из 4 вариантов ответа:
1) 
2) 
3) 
4) 
Верный ответ (1 б.): 1;
Задание # 52 - ошибка!
Вопрос:
Радиус окружности  равен …
равен …
Выберите один из 4 вариантов ответа:
1) 2
2) 
3) 4
4) 
Верный ответ (1 б.): 1;
Задание # 53 - ошибка!
Вопрос:
Точка пересечения прямой  и гиперболы
и гиперболы  имеет координаты …
имеет координаты …
Выберите один из 4 вариантов ответа:
1) 
2) 
3) 
4) 
Верный ответ (1 б.): 1;
Задание # 54 - ошибка!
Вопрос:
Мнимая полуось гиперболы  равна …
равна …
Выберите один из 4 вариантов ответа:
1) 3
2) 36
3) 6
4) 9
Верный ответ (1 б.): 1;

