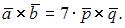Тема: Линейные операции над векторами
Вектор 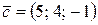 является линейной комбинацией векторов
является линейной комбинацией векторов 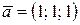 и
и 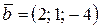 . Если
. Если 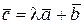 ,
, 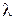 равно …
равно …
Решение:
Находим 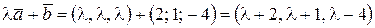 . Так как
. Так как 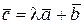 , то
, то 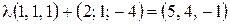 . Отсюда
. Отсюда 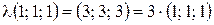 . Следовательно,
. Следовательно, 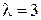 .
.
49. Тема: Линейные операции над векторами
Дан треугольник 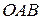 . Векторы
. Векторы 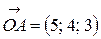 ,
, 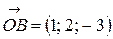 . Тогда вектор
. Тогда вектор 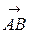 имеет координаты…
имеет координаты…
Решение:
Так как 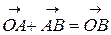 , то
, то 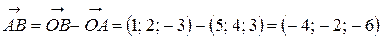 .
.
50. Тема: Скалярное произведение векторов
Дан вектор 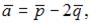 где
где 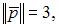
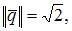 угол между векторами
угол между векторами 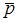 и
и 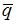 равен
равен 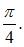 Тогда модуль вектора
Тогда модуль вектора 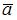 будет равен …
будет равен …
 |  | 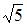 | |
 | 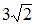 | ||
 | 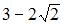 | ||
 |
Решение:
Так как 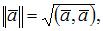 то
то 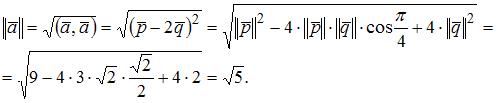
Тема: Скалярное произведение векторов
В ортонормированном базисе заданы векторы 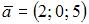 и
и 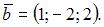 Тогда проекция вектора
Тогда проекция вектора 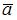 на вектор
на вектор 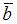 будет равна …
будет равна …
 |  | ||
 | |||
 | 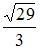 | ||
 | 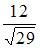 |
Решение:
Проекция вектора 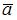 на вектор
на вектор 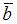 находится по формуле
находится по формуле
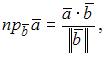
где 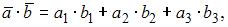
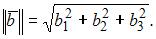
В нашем случае 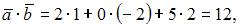
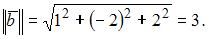
Следовательно, 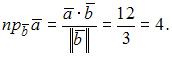
51. Тема: Скалярное произведение векторов
Скалярное произведение векторов 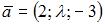 и
и 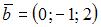 будет равно
будет равно 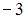 при
при 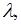 равном …
равном …
 |  | – 3 | |
 | – 6 | ||
 | |||
 |
Решение:
Скалярное произведение векторов 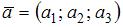 и
и 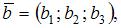 заданных своими координатами, равно:
заданных своими координатами, равно:
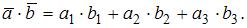
В нашем случае 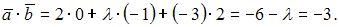 Откуда
Откуда 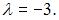
52. Тема: Скалярное произведение векторов
Даны точки 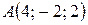 и
и 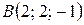 .
.
Скалярное произведение радиусов-векторов этих точек равно …
Решение:
Скалярное произведение векторов 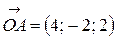 и
и 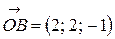 , заданных своими координатами, равно:
, заданных своими координатами, равно:
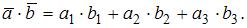
В нашем случае 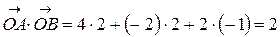 .
.
53. Тема: Скалярное произведение векторов
Даны точки 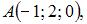
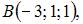
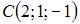 и
и 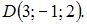 Тогда скалярное произведение векторов
Тогда скалярное произведение векторов 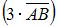 и
и 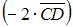 будет равно …
будет равно …
 |  | – 18 | |
 | – 15 | ||
 | |||
 |
Решение:
Скалярное произведение векторов 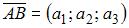 и
и 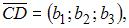 заданных своими координатами, равно:
заданных своими координатами, равно:
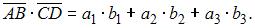
В нашем случае 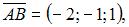
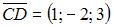 и
и 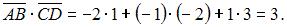
Тогда 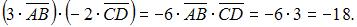
54. Тема: Скалярное произведение векторов
Даны точки 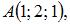
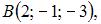
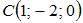 и
и 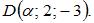 Скалярное произведение векторов
Скалярное произведение векторов 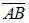 и
и 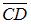 будет равно
будет равно 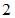 при
при 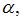 равном …
равном …
 |  | ||
 | – 3 | ||
 | |||
 | – 6 |
Решение:
Скалярное произведение векторов 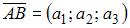 и
и 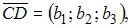 заданных своими координатами, равно
заданных своими координатами, равно 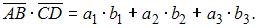
В нашем случае 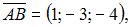
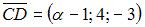 и
и 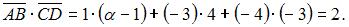 Тогда
Тогда 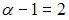 и
и 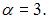
55. Тема: Скалярное произведение векторов
В ортонормированном базисе заданы векторы 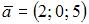 и
и 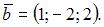 Тогда проекция вектора
Тогда проекция вектора 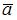 на вектор
на вектор 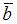 будет равна …
будет равна …
 |  | ||
 | |||
 | 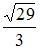 | ||
 | 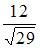 |
Решение:
Проекция вектора 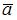 на вектор
на вектор 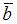 находится по формуле
находится по формуле
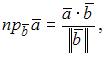
где 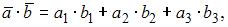
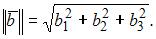
В нашем случае 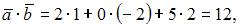
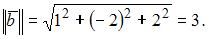
Следовательно, 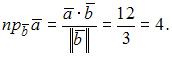
56. Тема: Скалярное произведение векторов
Векторы 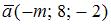 и
и 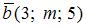 перпендикулярны при m, равном …
перпендикулярны при m, равном …
Варианты ответов:
- 1) 2
- 2) – 1
- 3) 2,5
- 4) – 2
57. Тема: Скалярное произведение векторов
Векторы 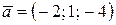 и
и 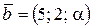 будут взаимно перпендикулярны, если значение параметра
будут взаимно перпендикулярны, если значение параметра 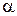 равно…
равно…
Решение:
Векторы 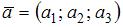 и
и 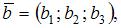 будут взаимно перпендикулярны, если скалярное произведение этих векторов равно 0:
будут взаимно перпендикулярны, если скалярное произведение этих векторов равно 0:
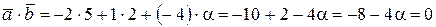 .
.
Отсюда 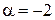 .
.
58. Тема: Скалярное произведение векторов
Скалярное произведение векторов 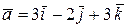 и
и 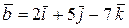 равно …
равно …
- 1) 2
- 2) – 1
- 3) 2,5
- 4) – 2
· Решение:
Скалярное произведение векторов 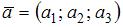 и
и 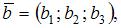 заданных своими координатами, равно:
заданных своими координатами, равно:
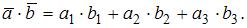
В нашем случае 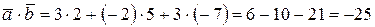 .
.
59. Тема: Векторное произведение векторов
Площадь треугольника с вершинами в точках 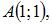
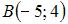 и
и 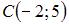 равна …
равна …
 |  | 7,5 | |
 | |||
 | |||
 | 2,5 |
Решение:
Площадь S треугольника ABC равна 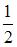 модуля векторного произведения векторов
модуля векторного произведения векторов 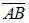 и
и 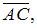 то есть
то есть 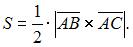 В нашем случае
В нашем случае 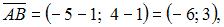
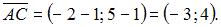 Тогда
Тогда 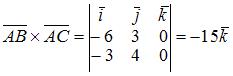 и
и 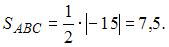
60. Тема: Векторное произведение векторов
Векторное произведение векторов 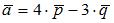 и
и 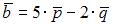 равно …
равно …
 |  | 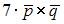 | |
 | 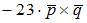 | ||
 | 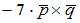 | ||
 | 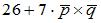 |
Решение:
Вычислим
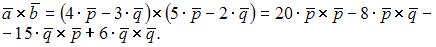
Так как 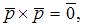
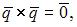
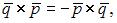 то
то