Свойства линейно зависимых и линейно независимых векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора 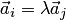, то она линейно зависима.

4. Система из 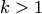векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов 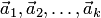линейно независима, а после присоединения к ней вектора 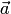оказывается линейно зависимой, то вектор 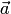можно разложить по векторам 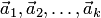, и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

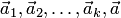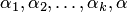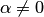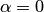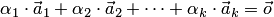Докажем, например, последнее свойство. Так как система векторов — линейно зависима, то существуют числа , не все равные 0, что . В этом равенстве . В самом деле, если , то . Значит, нетривиальная линейная комбинация векторов 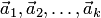равна нулевому вектору, что противоречит линейной независимости системы 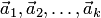. Следовательно, 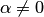и тогда 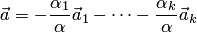, т.е. вектор 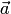есть линейная комбинация векторов 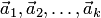. Осталось показать единственность такого представления. Предположим противное. Пусть имеется два разложения 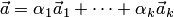и 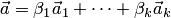, причем не все коэффициенты разложений соответственно равны между собой (например, ).

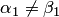Тогда из равенства 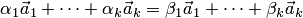получаем .

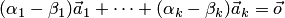Следовательно, линейная комбинация векторов 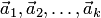равна нулевому вектору. Так как не все ее коэффициенты равны нулю (по крайней мере 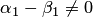), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов 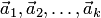. Полученное противоречие подтверждает единственность разложения.

2)МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Обозначим: S(x, t) - минимальное значение критерия качества Jt из (5) для оптимального процесса, начинающегося в момент t в точке x(t) = x. Этот процесс можно представить состоящим из двух участков: первого шага, на котором выбирается управление u(t) = u, и остальной части (от момента t + 1 до конца процесса). Вклад в критерий качества первого участка процесса равен R(x, u), а вклад второго участка можно, согласно принципу оптимальности, выразить через введенную выше функцию S в виде S(x(t + 1), t + 1). Учитывая, что управление на первом участке должно выбираться из условия минимизации критерия Jt при ограничении (1), получим равенство

Здесь и далее для определенности предполагаем, что функция S, как и ранее введенные в (2), (4) функции f, R, F, непрерывна. Подставляя в полученное соотношение равенство (2), получим основное соотношение метода динамического программирования

t = 0, 1, _, N - 1. (6)

Для оптимального процесса, начинающегося в момент t = N, критерий оптимальности (5) сводится к одному последнему слагаемому. Поэтому имеем

S(x, N ) = F (x). (7)

Соотношение (6) и условие (7), играющее роль начального условия, дают возможность последовательно определить функции S(x, t) при t = N - 1, _ _, 1, 0, а также рассчитать оптимальное управление и оптимальные траектории. Это достигается при последовательной реализации попятной и прямой процедур динамического программирования.

Алгоритм метода динамического программирования
1. Составляется уравнение Беллмана

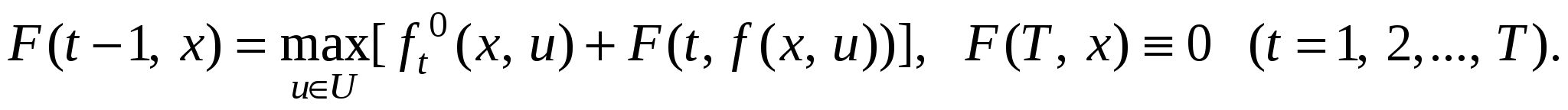
2. Путем решения в обратном времени уравнения Беллмана («обратный ход») находятся условно-оптимальные управления u*(t, x), а также функции Беллмана F(t, x) (t = T, T – 1, …, 1).
3. С помощью рекуррентных уравнений «прямого хода»


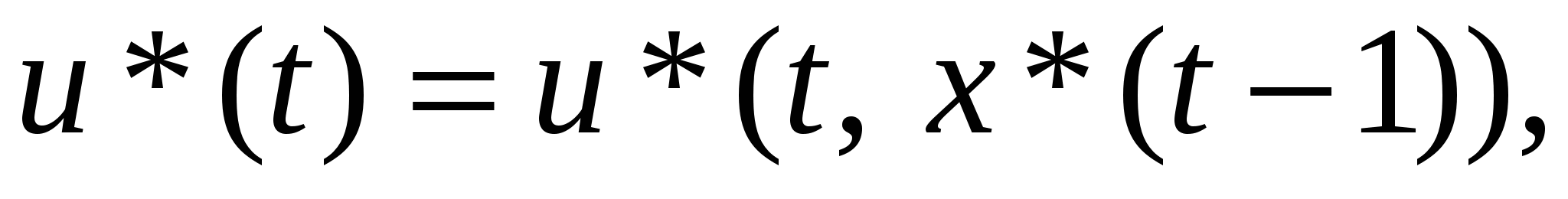
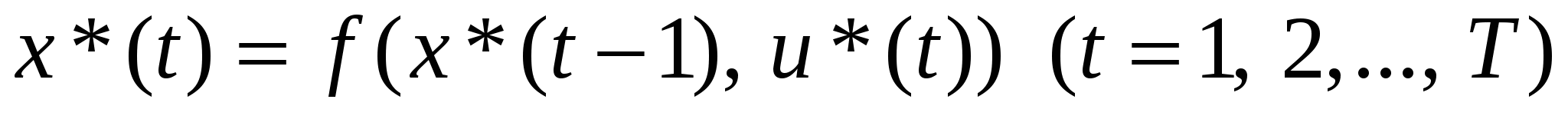
определяются оптимальные управления u*(t) и оптимальная траектория движения дискретной динамической системы x*(t) (t = 1, 2, …, T).
4. Находится оптимальное значение показателя качества управления F(0, x⁰).
Замечание. Так как аналитические выражения для условно-оптимальных управлений u*(t, x) при решении практических задач получаются редко, то их обычно табулируют, используя некоторую сетку по переменной х. А при вычислении оптимальных управлений 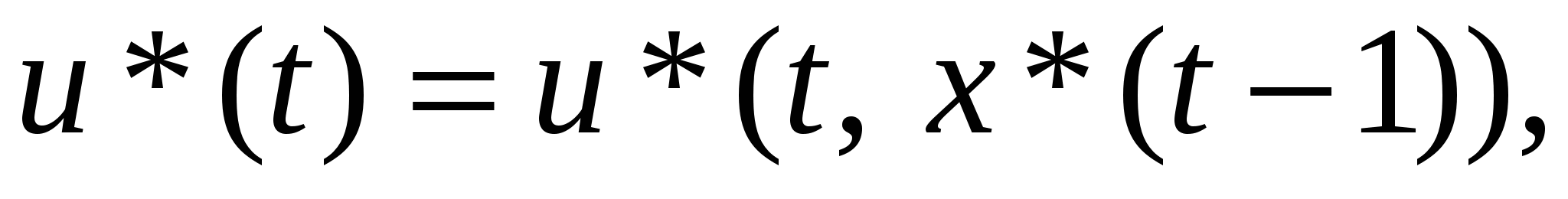при необходимости, применяют один из алгоритмов интерполяции.

Пример применения метода динамического программирования

Пусть имеется фирма, состоящая из двух предприятий. Рассмотрим задачу оптимального распределения средств фирмы на протяжении Т лет. На начало планового периода фирма располагала средствами x(0) = x⁰.

Деятельность предприятий организована таким образом, что средства u, вложенные в предприятие i (i = 1, 2), приносят в течение года доходf_i(u), причем часть дохода поступает в централизованный фонд фирмы. Средства из этого фонда x(t – 1) (t = 1, 2, …, T) в начале годаt определенным образом перераспределяются между предприятиями и идут на их развитие. Обозначим через u_i(t) (i = 1, 2) cредства, выделяемые для развития предприятиям в начале года t. Предполагается, что средства централизованного фонда полностью расходуются:

Состоянием фирмы будем считать переменную x(t), в качестве управляющих переменных возьмем u₁(t) и u₂(t). Тогда изменение состояния фирмы будет описываться уравнением

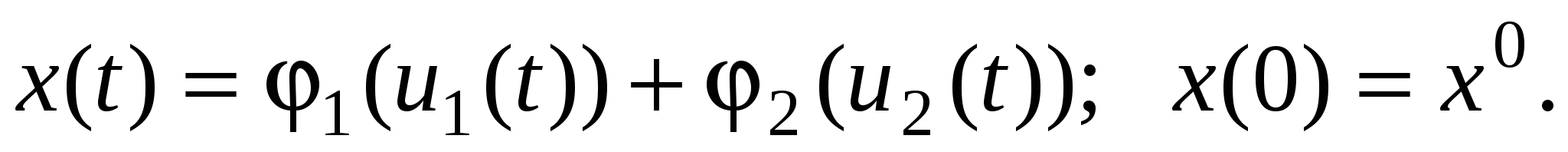
Управляющие воздействия удовлетворяют ограничению

Показателем качества управления является суммарный доход, полученный от деятельности предприятий в течение Т лет:

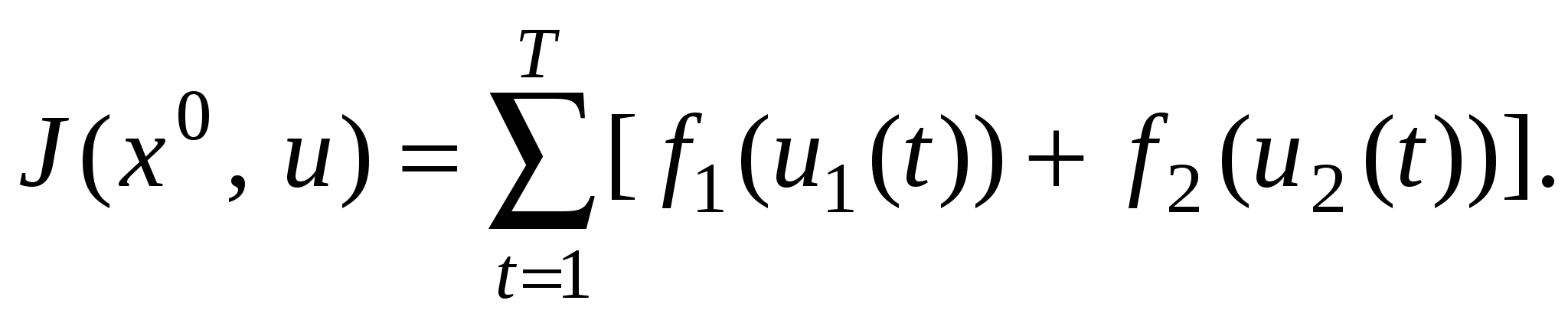
Приходим к следующей задаче оптимального управления:

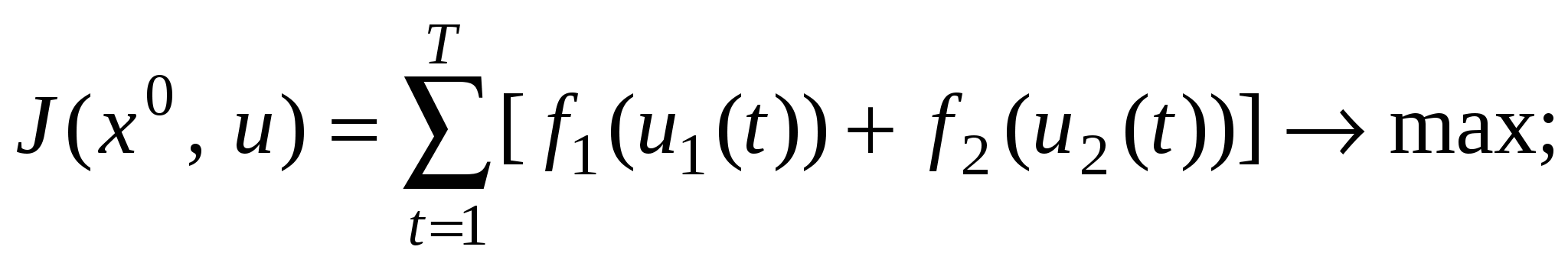
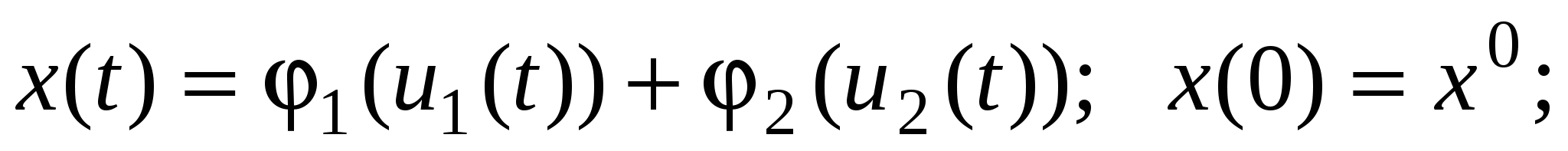
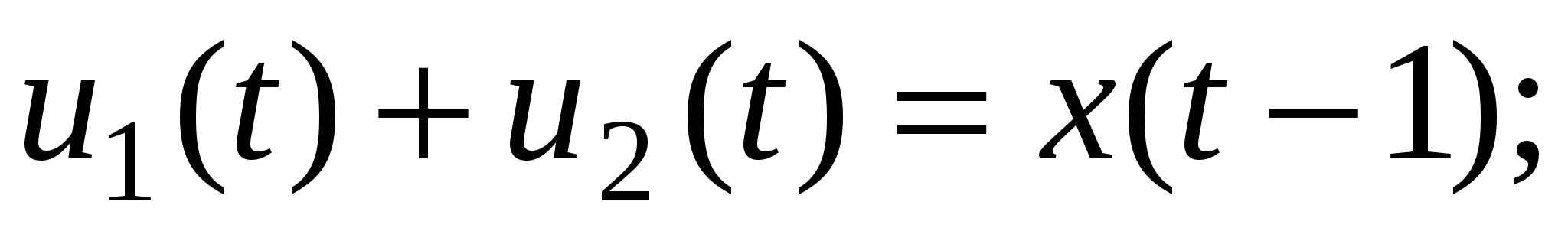
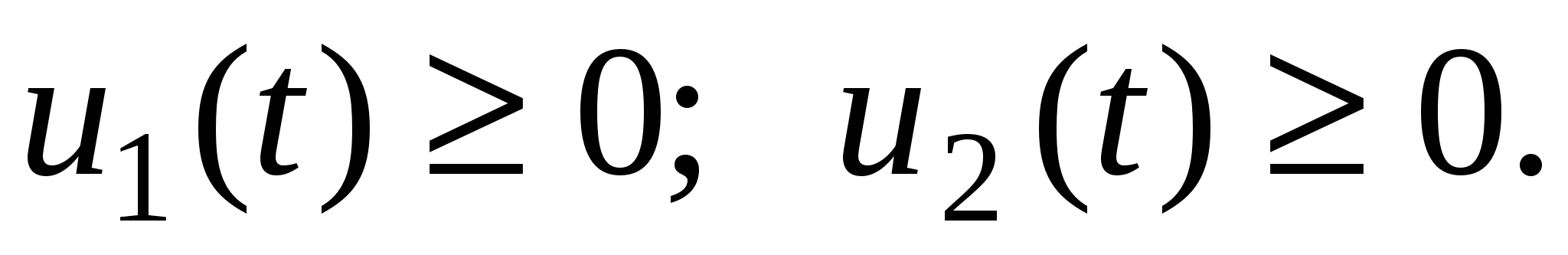
3) Ваша матрица

Знак	№	A1	A2	A3	A4
+		-2
			-1
	-5
		-1		-3

Занулили элементы в 1-ом столбце под 1-ым элементом

Знак	№	A1	A2	A3	A4
+		-2
		1.5	3.5
		-0.5	-4.5	-5

Занулили элементы в 2-ом столбце под 2-ым элементом

Знак	№	A1	A2	A3	A4
+		-2
		1.5	3.5
			-3.333333333333333	-3.333333333333333
			5.666666666666666	-2.3333333333333335

Занулили элементы в 3-ем столбце под 3-им элементом

Знак	№	A1	A2	A3	A4
+		-2
		1.5	3.5
			-3.333333333333333	-3.333333333333333
				-8

Перемножили элементы главной диагонали

Знак	№	A1	A2	A3	A4
+		-2
		1.5	3.5
			-3.333333333333333	-3.333333333333333
				-8

(-2) * 1.5 * (-3.333333333333333) * (-8) = -80

БИЛЕТ 25

1)ЕДИНИЧНАЯ МАТРИЦА [unit matrix, identity matrix] — такая квадратная матрица, у которой все элементы поглавной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, напр.:

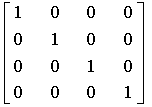
2)Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Метод был разработан математиком Джорджом Данцигом в 1947 году.

Модифицированный симплекс-метод

В модифицированном методе матрица

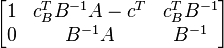
не пересчитывается, хранится и пересчитывается только матрица 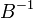. В остальном алгоритм похож на вышеописанный.

1. Вычисляем двойственные переменные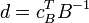

2. Проверка оптимальности. 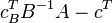преобразуется в .

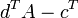Проверка заключается в вычислении 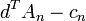для всех столбцов 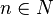. Столбец со значением < 0 можно вводить в базис.

Часто выбирают минимальное значение, но для этого нужно перебрать все столбцы.

Чаще выбирают значение, меньшее некоторого заданного значения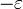

Если такого столбца не обнаружится, за принимается максимальное найденное абсолютное значение и соответствующий столбец 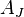вводится в базис.

3. Определение выводимого.

Пусть 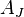- вводимый столбец, соответствующий переменной 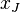Базиный план - это решение системы 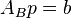Увеличиваем .

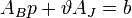Умножим слева на , т.е. .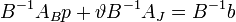

Здесь 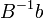- базисный план, 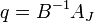- разложение вводимого столбца по базису.

Находим максимальное значение 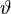, при котором все значения не отрицательны. Если 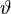может быть взято как угодно велико, решение не ограничено. В противном случае один из элементов выйдет на нулевое значение. Выводим соответствующий столбец из базиса.

4. Пересчет опорного(базисного) плана.

Вычисляем новый опорный план по уже приведенной формуле 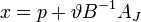с найденным значением .

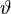5. Пересчитываем обратную к базисной .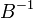

Пусть 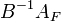- выводимый столбец.

Матрица B представима в виде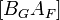

где 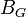- базисная матрица без выводимого столбца.

После замены столбца базисная матрица будет иметь вид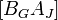

Нам нужно найти матрицу 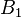, такую что

=> => =>

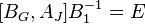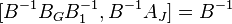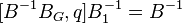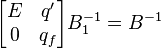
Откуда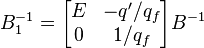

Замечание.

При пересчете матрицы 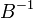накапливаются ошибки округления. Во избежание получения больших ошибок время от времени матрица пересчитывается полностью. Этот процесс называется "повторением".

3)Задание. Для матрицы 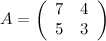найти обратную методом присоединенной матрицы.

Решение. Приписываем к заданной матрице 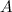справа единичную матрицу второго порядка:

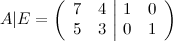
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):

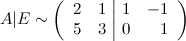
От второй строки отнимаем две первых:

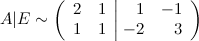
Первую и вторую строки меняем местами:

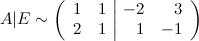
От второй строки отнимаем две первых:

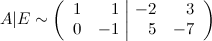
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:

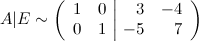
Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.

Таким образом, получаем, что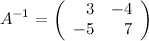

Ответ.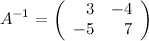

Билет № 26

1) Дать правило расчета определителя матрицы размерности 2 х 2