Скорректированный индекс множественной детерминации

Индекс множественной детерминации используют для определения качества регрессии, чем больше 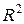, к единице тем выше качество подбора регрессии.

Но использование только одного индекса детерминации для определения наилучшего уравнения регрессии недостаточно. Необходимо учитывать, что при увеличении факторов включенных в уравнение регрессии, при одном и том же числе наблюдений 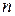, при расчете показателей корреляции, за счет использования остаточной дисперсии появляется систематическая ошибка – чем больше число параметров в уравнении регрессии, при одном и том же числе наблюдений 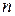, тем больше получается расчетный показатель тесноты связи. Если число факторов приближается к числу наблюдений, то расчетный показатель корреляции будет близок к единице, то есть показывать тесную связь, даже если связь незначительна. Для того чтобы избежать этого рассчитывают скорректированный индекс множественной детерминации.

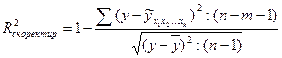(9.153)

или

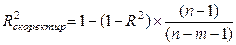(9.154)

Скорректированный индекс множественной корреляции рассчитывают соответственно как:

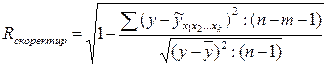(9.155)

или

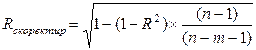(9.156)

где:

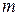- для линейной множественной модели – число факторов включенных в регрессионную модель. Для нелинейной модели 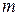- число параметров при 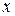и их линеаризации ( 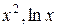и так далее), которое может быть больше числа факторов.

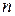- число наблюдений.

В силу сказанного выше необходимо понимать, что нельзя перегружать множественную модель факторами, так как снижается достоверность расчетов, принято считать, что на каждые 8-10 наблюдений в модель целесообразно включать один фактор.

Частная корреляция

Множественный коэффициент (индекс) корреляции показывает тесноту связи между результатом и всеми включенными в модель факторами, для того, чтобы изучить силу связи между результатом и только одним из включенных в модель факторов, рассчитывают частные коэффициенты корреляции, для каждого из факторов включенных в модель.

Частный коэффициент корреляции показывает тесноту связи между результативным признаком 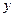и только одним фактором 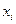при элиминировании (устранении) влияния всех остальных включенных в модель факторов.

В зависимости от того, влияние скольких факторов необходимо исключать различают частные коэффициенты разных порядков: нулевого, первого, второго, третьего и т.д. Так, например:

· Коэффициенты частной корреляции нулевого порядка – коэффициенты парной корреляции, так как нет необходимости устранять влияние даже одного фактора.

· Коэффициенты частной корреляции первого порядка – коэффициенты частной корреляции, в которых элиминируется влияние одного фактора ( 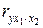, , 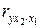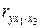и т.д.).

· Коэффициенты корреляции второго порядка – коэффициенты частной корреляции, в которых элиминируется влияние двух факторов ( 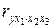, , 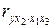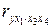и т.д.) и так далее.

Коэффициенты частной корреляции более высоких порядков рассчитываются через коэффициенты корреляции более низких порядков. Коэффициенты первого порядка через коэффициенты нулевого порядка, второго порядка через коэффициенты первого порядка и т.д. Рекуррентная формула для расчета коэффициентов частной корреляции 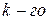порядка имеет вид:

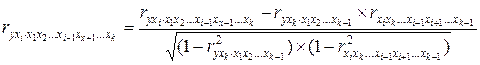(9.157)

Коэффициенты частной корреляции могут принимать значения в пределах от -1 до 1.

Также частные коэффициенты корреляции можно рассчитать через множественные коэффициенты детерминации. Так коэффициент частной корреляции второго порядка рассчитывается как:

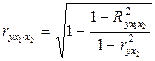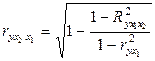или и т.д. (9.158)

В общем виде уравнение для расчета коэффициентов частной корреляции 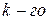порядка имеет вид:

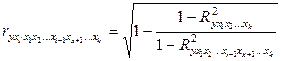(9.159)

где

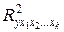- коэффициент множественной детерминации 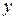для всех факторов.

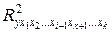- коэффициент множественной детерминации без включения в модель фактора .

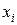Рассчитанные через множественные коэффициенты детерминации частные коэффициенты корреляции могут принимать значения в интервале от 0 до 1.

Кроме того, частные коэффициенты корреляции можно рассчитать через 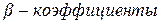. Так, например, частные коэффициенты корреляции первого порядка для двухфакторной линейной модели, выраженной в стандартизованном масштабе :

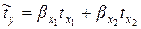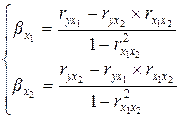(9.160)

Отсюда:

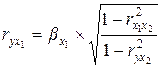и 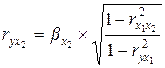(9.161)

Возводя в квадрат коэффициенты частной корреляции, получают коэффициенты частной детерминации.

Частные коэффициенты корреляции используют при формировании корреляционно-регрессионной модели, для отбора факторов. При этом из модели исключают факторы несущественные по критерию Стьюдента.

Коэффициент частной детерминации показывает долю вариации результативного признака дополнительно сложившуюся при включении в модель фактора 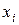, в вариации признака, не объясненную включенными до этого в модель факторами. Можно рассчитать по формуле на основе коэффициентов множественной детерминации.

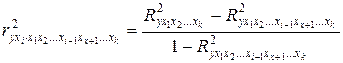(9.162)

где

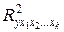- коэффициент множественной детерминации 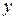для всех факторов.

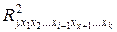- коэффициент множественной детерминации без включения в модель фактора .

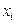Зная коэффициенты частной детерминации, последовательно нулевого, первого, второго и более высоких порядков, определяют коэффициент множественной корреляции.

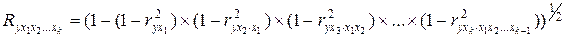(156)

1.9.4.7 Оценка надежности параметров множественной регрессии и корреляции

Оценка значимости множественного уравнения регрессии в целом проводится с помощью 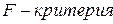, (критерия Фишера).

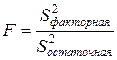(9.163)

где:

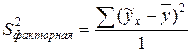– факторная дисперсия (9.164)

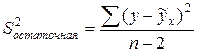– остаточная дисперсия (9.165)

F-критерий можно рассчитать и по формуле:

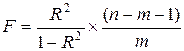(9.166)

где:

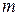- для линейной множественной модели – число факторов включенных в регрессионную модель. Для нелинейной модели 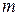- число параметров при 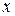и их линеаризации ( 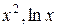и так далее), которое может быть больше числа факторов

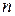- число наблюдений

Если расчетный 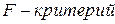превышает табличный при определенном уровне значимост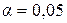и или 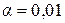, и числе свободы - 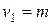, 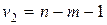(таблицы Снедекора-Фишера – приложение 2) можно сказать, что уравнение множественной регрессии статистически значимо.

Величина 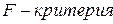позволяет также оценить статистическую значимость и коэффициента (индекса) множественной корреляции .

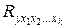Кроме оценки уравнения в целом, большое практическое значение имеет статистическая оценка значимости каждого отдельно включенного в модель фактора, через частные критерии Фишера 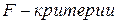, ( 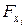). Данная оценка позволяет оценить целесообразность включения в модель множественной регрессии каждого из факторов после введения в модель остальных факторов.

Расчет частного 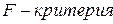, для фактора 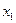проводится по формуле:

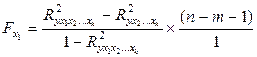(9.167)

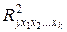- коэффициент множественной детерминации для модели, включающей все факторы

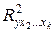- коэффициент множественной детерминации для модели, без включения фактора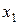

Расчета частного 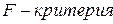в общем виде, для фактора 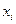проводится по формуле:

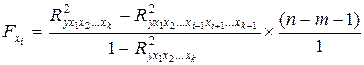(9.168)

Расчета частного 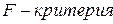, для оценки значимости влияния фактора 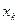после включения в модель других факторов проводится по формуле:

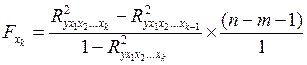(9.169)

Если величина расчетного частного 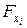превышает величину табличного при определенном уровне значимост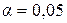и или 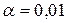, и числе свободы - 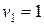, 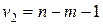(таблицы Снедекора-Фишера – приложение 2), можно сказать, что включение в модель фактора 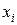, после введения в модель остальных факторов, целесообразно. Если величина расчетного частного 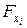меньше табличного значения, можно сказать, что включение в модель фактора 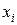, после введения в модель остальных факторов, статистически неоправданно, и его необходимо исключить из рассматриваемой модели.

Зная величину частного критерия Фишера 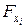, рассчитывают частные критерии Стьюдента, для определения значимости каждого из коэффициентов чистой регрессии .

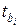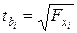(9.170)

Критерий Стьюдента 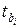также можно рассчитать по формуле:

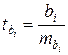(9.171)

где:

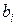- коэффициент чистой регрессии для фактора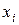

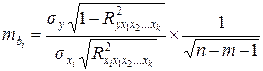- стандартная ошибка 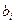(9.172)

где:

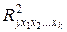- коэффициент детерминации множественного уравнения регрессии

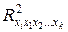- коэффициент множественной детерминации зависимости фактора 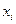со всеми остальными факторами уравнения множественной регрессии

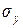- среднеквадратическое отклонение результативного признака

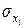- среднеквадратическое отклонение факторного признака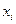

Полученные фактические значения критерия Стьюдента сравнивают с табличными значениями при определенном уровне значимост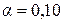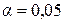и , или 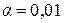, и числе степеней свободы 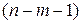(приложение 1). Если фактическое значение 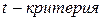больше табличного соответствующий коэффициент регрессии статистически значим.

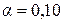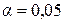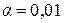Фактические значения критерия Стьюдента сравнивают с табличными значениями при определенном уровне значимости , или , и числе степеней свободы 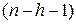, где 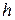- число исключенных переменных (приложение 1). Если фактическое значение 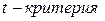больше табличного соответствующий коэффициент частной корреляции статистически значим.