Модульная единица 1.8. Выборочный метод

Выборочное наблюдение – несплошное наблюдение, при котором исследованию подвергается лишь часть единиц изучаемой совокупности, отобранная в определенном порядке.

Вся совокупность, по которой проводится исследование, называется генеральной совокупностью.

Отобранные единицы генеральной совокупности для непосредственного анализа называются выборочной совокупностью (выборка).

Генеральная совокупность может быть реальной, а может быть гипотетической, включающей случаи, которые реально не существуют, например, все возможные результаты эксперимента.

В выводной статистике принято строго различать параметры и свойства генеральной совокупности и их оценки по данным выборки. С этой целью принята следующая система обозначений - табл. 8.1.

Таблица 8.1

Показатель	Генеральная совокупность	Выборка
Средняя величина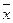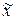
Доля альтернативного признака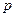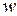
Дисперсия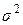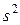
Объем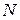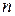

1.8.1 Методы и способы отбора, обеспечивающие репрезентативность выборки

Условия отбора в выборочную совокупность, которые обеспечат репрезентативность (представительность,) выборки:

Первое условие – равная для каждой единицы гене­ральной совокупности возможность попасть в выборку.

Второе условие – достаточная численность выборочной сово­купности. Чем больше единиц обследовано, тем точнее суждение о генеральной совокупности, тем меньше ошибки выборки.

Случайный отбор (повторный или бесповторный) используется, когда в генеральной совокупности разли­чия единиц по изучаемым признакам носят количественный харак­тер, единица наблюдения и учетная единица совпадают, предва­рительное расположение единиц в каком-либо порядке невозможно или нецелесообразно.

При случайном повторном отборе каждая единица отбирается из генеральной совокупности в случайном порядке наугад, и после записи значения возвращается в генеральную совокупность. При этом отдельные единицы могут повторно попасть в выборку.

При случайном бесповторном отборе каждую единицу, отобранную в случайном порядке из генеральной совокупности, после записи значения изучаемого признака не возвращают обратно и, таким образом, каждая единица может попасть в выборку только один раз.

Механический отбор осуществляется механически, т.е. через определен­ное число единиц или в другом заданном порядке. Например, надо сформировать выборку из 100 единиц, а численность генеральной совокупности 1000, следовательно, в выборку должна попасть каждая десятая единица.

Типический отбор необходимо использовать в том случае, если в генеральной совокупности объективно существуют качественно своеобразные группы единиц. Вся генеральная совокупность при этом способе отбора предварительно разбивается на группы (ти­пы).

Затем из каждой группы, учитывая, как правило, нормальный характер распределения единиц в них, в порядке случайного или механического отбора формируется выборка. При этом число единиц, отобранных из каждой группы в выборочную совокупность, должно быть пропорционально или численности групп, или их средним квадратическим отклонениям, или дисперсиям изучаемо­го признака. При таком способе повышается надежность резуль­татов выборки, поскольку обеспечено более пропорциональное представительство каждой группы.

Серийный отбор – из генеральной совокупности путем случайной бесповторной или механической выборки отбирают сразу группы единиц; их называют сериями или гнездами. Общее число серий, составляющих генеральную совокупность, рассматривается как ее общая численность, а количество отобранных серий составляет численность выборки.

1.8.2 Ошибки выборочного наблюдения

Разность между показателями выборочной и генеральной совокупности называетсяошибкой выборки.

Ошибки регистрации возникают из-за неправильных или неточных сведений. Среди ошибок регистрации выделяются систематические, обусловленные причинами, действующими в каком-то одном направлении и искажающими результаты работы (например, округление цифр, тяготение к полным пятеркам, десяткам, сотням и т. д.), случайные, проявляющиеся в различных направлениях, уравновешивающие друг друга и лишь изредка дающие заметный суммарный итог.

Ошибки репрезентативности (разность между характеристиками выборочной и генеральной совокупностей) также могут быть систематическими и случайными. Систематические ошибки репрезента­тивности возникают из-за неправильного, тенденциозного отбора единиц, при котором нарушается основной принцип научно организованной выборки – принцип случайности. Случайные ошибки репрезентативности означают, что, несмотря на принцип случайности отбора единиц, все же имеются расхождения между характеристиками выборочной и генеральной совокупности. В общем можно сказать, что ошибки репрезентативности – это разница между значением показателя, рассчитанного по выборке и соответствующим генеральным показателем. Например:

· ошибка репрезентативности средней равна:

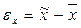, (8.1)

· ошибка репрезентативности выборочной относительной величины:

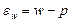, (8.2)

· ошибка репрезентативности дисперсии:

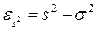, (8.3)

1.8.3 Определение средней ошибки выборочного наблюдения

Средняя ошибка выборочной средней при случайном повторном отборевыборочной средней рассчитывается по формуле:

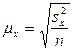, (8.4)

где 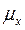– средняя ошибка выборочной средней;

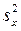– дисперсия выборочной совокупности;

n – численность выборки.

Между дисперсиями в генеральной и выборочной совокупностях существует следующее соотношение:

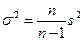, (8.5)

Если 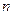достаточно велико, то 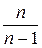близко к единице, этим сомножителем можно пренебречь и генеральную дисперсию можно заменить выборочной дисперсией.

Средняя ошибка выборочной доли при случайном повторном отборе:

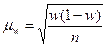, (8.6)

Средняя ошибка выборочной средней при случайном бесповторном отборе:

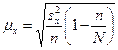, (8.7)

где 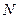– численность генеральной совокупности.

Средняя ошибка выборочной доли при случайном бесповторном отборе:

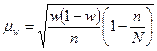, (8.8)

где 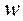– доля единиц, имеющих изучаемый признак;

n – численность выборки;

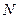– численность единиц генеральной совокупности.

1.8.4 Определение предельной ошибки выборочного наблюдения

Отклонение выборочной средней (доли) от генеральной средней (доли) с какой-то вероятностью 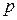называется предельной ошибкой выборки.

Предельная ошибка выборки 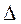связана со средней ошибкой выборки 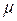отношением:

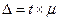, (8.9)

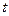– коэффициент кратности ошибки (коэффициент доверия) выборки зависит от вероятности 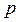, с которой гарантируется, что величина предельной ошибки не превысит 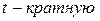среднюю ошибку.

Таблица 8.2 - Значение гарантированного коэффициента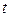

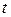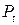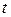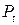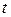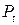1,00	0,6827	1,70	0,9109	2,40	0,9836
1,10	0,7287	1,80	0,9281	2,50	0,9876
1,20	0,7699	1,90	0,9426	2,60	0,9907
1,30	0,8064	2,00	0,9545	2,70	0,9931
1,40	0,8385	2,10	0,9643	2,80	0,9949
1,50	0,8664	2,20	0,9722	2,90	0,9963
1,60	0,8904	2,30	0,9786	3,00	0,9973

При бесповторном отборе предельная ошибка для выборочной долиопределяется как:

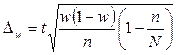, (8.10)

При бесповторном отборе предельная ошибка выборочной средней определяется как:

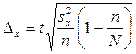, (8.11)

При повторном отборе предельная ошибка выборочной доли определяется как:

, (8.12)

При повторном отборе предельная ошибка выборочной средней определяется как:

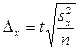, (8.13)

1.8.5 Определение необходимой численности выборки

Необходимая численность выборки при повторном отборе для выборочной средней рассчитывается как:

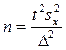, (8.14)

Необходимая численность выборки при повторном отборе для выборочной доли рассчитывается как:

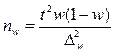, (8.15)

Необходимая численность выборки при бесповторном отборе для выборочной средней рассчитывается как:

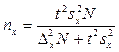, (8.16)

Необходимая численность выборки при бесповторном отборе для выборочной доли рассчитывается как:

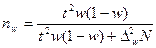, (8.17)

1.8.6 Малая выборка

Малая выборка – выборка, объем которой не превышает 30 единиц.

Средняя ошибка малой выборки 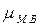рассчитывается как:

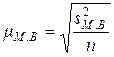, (8.18)

где 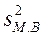– дисперсия малой выборки.

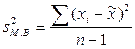, (8.19)

Предельная ошибка малой выборки 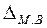определяется как:

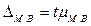(8.20)

В малых выборках коэффициент доверия 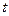зависит не только от заданной доверительной вероятности. Согласно распределению Стьюдента, вероятность того, что предельная ошибка не превысит 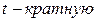среднюю ошибку, зависит и от величины 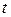, и от численности выборки n. Для отдельных значений 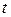и n доверительная вероятность малой выборки рассчитывается по специальным таблицам Стьюдента, в которых даны распределения стандартизированных отклонений:

1.8.7 Способы распространения характеристик выборки на генеральную совокупность

Способ прямого пересчета – показатели выборочной доли 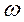или средней 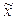распространяются на генеральную совокупность с учетом ошибки выборки.

Способ поправочных коэффициентов – после обобщения данных сплошного учета практикуется 10%-е выборочное обследование с определением так называемого «процента недоучета».

Таблица 8.3 - Распределение вероятности в малых выборках в зависимости от значения коэффициента доверия 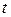и численности выборки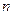

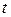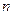	0,626	0,644	0,656	0,662	0,666	0,668	0,670
1,5	0,792	0,816	0,832	0,838	0,846	0,848	0,850
2,0	0,884	0,908	0,924	0,930	0,936	0,938	0,940
2,5	0,933	0,953	0,966	0,970	0,975	0,977	0,978
	0,960	0,976	0,984	0,988	0,991	0,992	0,992